


Next: About this document ...
Lecture 4
Mass and Energy
To give Relativity a complete, self-consistent structure we must add a few more
"stones". From what we have learnt so far, a body cannot reach the speed of
light. It is legitimate to ask what prevents it from being accelerated beyond c.
Let us recall what Newton had to say :
A constant force will produce a constant acceleration , i.e.
F = m a
In a gedanken experiment, and within Newtonian Physics, we could think of
applying a constant force to a body, and so keep accelerating it past the
speed of light. This is obviously inconsistent with Relativity.
Parenthesis : The Physics of Star Trek (by Lawrence Krauss)
In Star Trek, the Enterprise can suddenly be accelerated to near c. Is this
realistic ? The human body can only sustain accelerations of a few times the
acceleration of gravity (i.e. a few "g's"). How long would it take to accelerate
a spaceship and its occupants, from 0 to c, with a constant acceleration of,
say, 10 g's?
Instant acceleration is therefore non-realistic, after the first episodes the
Star Trek script writers introduced "inertial dampers" to shield the crew
from lethal accelerations.
But let's go back to our problem. Remembering the meaning of acceleration :
Newton's law could be writtten as
In reality, as Newton knew himself, the correct expression is
For most practical cases the mass is constant so we do not have to worry about
its variation, even though exceptions can be found even in Newtonian Physics:
a standard problem given in Introductory Physics courses is to study the motion
of a train wagon full of sand, but with a hole on the floor from which sand
continuously escapes....
But what do we mean by mass ? In Classical Physics we can think of it
in two respects:
- 1.
- the mass of a body is something related to its quantity of matter
, i.e. something connected to the number of atoms (as well as the mass of each
atom...)
- 2.
- at the same time the mass is also a measure of the body's inertia, i.e.
its reluctance to having its velocity changed.
In Newtonian Physics these two pictures are interchangeable, but Einstein broke
this correspondance : in Relativity, the inertia of an object is not a constant
quantity, characteristic of each object, but it is a function of velocity :
where m0 is the rest mass, i.e. the mass of the object as measured
at rest (and related therefore to its "quantity of matter"). We can then
immediately see how velocities are going to be constraned below c : the more I
try to accelerate an object, the more it opposes my attempts, so that, in order
to accelerate it to c I would need to act upon it with an infinite Force (or
for an infinite time) and neither possibility is very practical...
Putting it all together :
if we use the standard notation 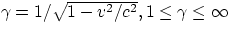 , then we can write :
Question :
, then we can write :
Question :
Can anything move at the speed of light ?
The answer is that masssless objects can (and do) move at the speed
of light. We can then distinguish between matter and radiation.
The relation between mass and velocity is verified matter-of-factly in any
Particle Accelerator, where sub-atomic particles going round and round a ring
are given repeated boosts of energy. After a while, the velocity of the particle
hardly increases, even though the periodic kicks do result in a gradual increase
of the particle's energy. There must then be a relation between the increase in
mass and the increase in energy, and of course we all know the answer :
E = m c2
which, from what we have seen, could be written as
This expression tells us two things :
- 1.
- the increase in (kinetic) energy of an accelerating body is not related
to an increase in velocity, but to an increase in mass
- 2.
- even a body at rest possesses a (potentially enormous) amount of energy,
given by E = m0c2 .
The relation between mass and energy is even more general than you might have
thought. It turns out that every time a system acquires a certain amount of
energy of whichever type (kinetic, gravitational, thermal, chemical, etc.), its
mass increases, according to Einstein's formula. Obviously for all everyday
instances, the mass differentials are completely below any measurable level.
Exceptions are nuclear phenomena, where mass losses become non negligible (i.e.
of the order of percent) and, moreover, masses can be measured without the need
of a scale...
Deferring to a later chapter the discussion of nuclear energy (from fission or
from fusion), we can for now amuse ourselves answering the following question:
is there some way to recover all (or at least most) of the energy contained in
the rest mass ?
The answer is yes, there are at least two processes, even though neither of them
is (yet?) very practical.
- 1.
- MATTER-ANTIMATTER ANNIHILATION
Sub-atomic Physics research has shown that every type of particle (proton,
neutron, electron, neutrino, muon, etc.) has its anti-particle partner.
Anti-particle are identical to their twin particles, except that all the
"charges" (e.g. electric charge) are of the opposite sign. Moreover, a particle-
antiparticle pair has an intriguing property : when they meet, they can
annihilate all of their mass into a blast of energy.
Unluckily, even though we know how to "create" antimatter, our procedures are
extremely inefficient. And, at best, we would get out of it as much energy as we
have to put in. A neat solution would be if we were to find an "antimatter
deposit" somewhere in the universe, but,as of today, the chances appear to be
exceedingly slim.
- 2.
- BLACK HOLE POWER STATION
Contrary to the original belief, i.e. that nothing can come out of it,
according to the current understanding, if we throw mass into a black hole, half
of it is spat out as radiative energy. Unluckily, it is even less likely that
such process will ever be practical.



Next: About this document ...
Sergio Conetti
2/10/1999