Physics 109 Homework Problems
Michael Fowler
Before Galileo
Following Thales: recall Thales learned in Egypt how to measure heights by measuring a shadow, and how to find distances of inaccessible objects by measuring angles and drawing scale model triangles. I want you to try this on the Grounds. You will need a ruler and a protractor. I think you should work in groups of two or three, but each of you should write up the homework by yourself, using notes if you like.
1. (a) Go to the point across Emmet from the Bookstore Parking Garage, where you'll see lamp posts like the one pictured below.Find the height of the lamp post by measuring the length of its shadow (pace it out) and comparing with your own shadow.


(b) Now look across the pond to the small archway structure (just visible in the picture above) beyond the pond near the left-hand side. Point a pencil at that arch from two different points on the Emmet sidewalk, measure the angles and the distance between the points, draw a scale diagram and deduce how far away the arch is from the Emmet sidewalk.
(c) Now go to the Lawn, the area on the same level as the Rotunda.The idea is to estimate the height of the Rotunda by drawing the right triangles. Notice from where I'm standing when I took this picture, some leaves are in line with the top of the Rotunda. I could find the

distance from where I'm standing to the base of the Rotunda (then I need to find what it is to the central point), then the distance from where I took the picture to the point directly under those leaves, and finally the height of the leaves. Or, I could look from ground level at a friend who walks to the point where the top of her head just blocks out the top of the Rotunda, and figure it from there.
2. Notice now that we could have found the height of the Rotunda even if we couldn't get to it: the distance to the Rotunda could have been determined by measuring angles to it from two different places, like the two ends of one of the paths going across the Lawn, just as the distance to the arch was found in the previous exercise. Could the Greeks have found the distance to the Moon in this way? Could we, with present-day technology?
3. How high does the Sun get in the sky at midday?(The high point is close to 1 pm since we're on EST.)By "how high" I mean an angle; which I want you to measure, by finding an upright object (like holding a pencil vertical) and marking off its shadow (easier to do with two of you!), then drawing a triangle.Or, you could angle a pencil towards the Sun so it has no shadow, then measure the angle it is making with the vertical (or horizontal - just be clear which one you mean in writing this up).
Given that Charlottesville is 38 degrees from the Equator, what would that angle be on Midsummer's day?On Midwinter's day? (This is a lot easier to figure out if you have a globe to look at - try to find one!)
4. Finding the angular size of the moon: choose some suitable round object, such as a dime, quarter, a tennis ball, ping pong ball or whatever, and while you are looking at the moon, have your partner hold the ping pong ball (say) at just the right distance that it looks to you exactly the same size as the moon. You could try it directly in front of the moon, to just block it, or side by side with the moon, whatever works best for you. Now, measure the distance from your eye to the ball, and measure the diameter of the ball. Given that the moon is 230,000 miles away, figure out the moon's diameter. What is the angular size of the moon? That is, if you take two pencils, point one at the bottom of the moon, and one at the top, as seen from here, what is the angle between them? You can answer in degrees or radians. (One radian is the angle of a piece of pie having the curved side the same length as the straight sides.)
5. Find the North Star (Polaris). Now, find how high Polaris is above the horizon by pointing a pencil directly at Polaris and having your partner measure the angle between the pencil and a horizontal line running directly beneath it.
Just after dark, find the Big Dipper, and sketch the Big Dipper together with Polaris. Three hours later, check them again. Has Polaris moved? Has the Big Dipper moved? Draw on your sketch how they have moved, if at all, in the sky.
6. Explain in a sentence or two, together with a simple diagram of the earth and the sun, why it is warmer in summer than in winter.
7. Some years ago, a very attractive photograph of the Rotunda viewed from the middle of the Lawnwas on sale, it was night and the full Moon was visible quite close to the Rotunda, so the shape of the Rotunda echoed the Moon. How could you prove this photo was a fake?
8. You set up base camp on a bear hunting expedition.You travel exactly twenty miles south, rest for a meal, then go twenty miles east, where you shoot a bear. Now you go twenty miles north and you are back at your base camp. What color was the bear? Give your reasoning.
9. Plato defined a regular solid as one with every edge the same length, and the same number of edges meeting at each vertex. Explain in your own words (but with diagrams) why there can only be five such solids.
10. Prove that the square root of three cannot be expressed as a ratio of whole numbers. (Hint: remember that any whole number can be expressed as a product of prime factors. The proof of the square root of two was all about odd and even numbers, this time concentrate of factors of 3, not 2.)
11. The autumnal equinox is on September 23 this year. Describe the path of the sun in the sky on that day, as seen from Charlottesville. Where, exactly does it rise? Where does it set? What is the angle of its maximum height in the sky? Use a globe, or imagine one, and draw a diagram to explain this angle. Now consider Melbourne, Australia, which happens to be just about as far south of the equator as we are north. Describe in similar detail the path of the sun through the sky as seen from Melbourne on that day. Finally, what is the path of the sun as seen from the South Pole research station on that day?
12. In a paragraph or so, summarize the differences between Plato and Aristotle in their approach to nature.
13. Explain briefly why there are seasons. Are there seasons on the equator? Explain. How much do you think the average high temperature each month varies on the equator? Which months would you expect to be warmest?Find some city near the equator and check out your answer.
14. These days, Mars is high in the sky at midnight. Could Venus ever be high in the sky at midnight? Explain your answer carefully.
15. On September 21, day and night will have equal length in Charlottesville. Where else on earth will that be true on that day? Explain. Where on earth will the sun be directly overhead at midday on that day?
16. You are in a garden somewhere on earth and you come across a sundial. Can you tell by looking at the sundial which hemisphere you are in?
17. The moon goes round the earth once a month. Explain briefly why we don't see an eclipse of the sun every month.
18. Go to the solar system simulator at http://space.jpl.nasa.gov/ Click the option to have the image take up 30% of the width.
Look at: Mars as seen from Earth, Earth as seen from Mars, Jupiter as seen from Earth, Earth as seen from Jupiter. Draw three concentric circles approximately representing Earth, Mars and Jupiter.Figure out, from the shadowing you see on the views you looked at, where the three planets must be in their orbits relative to each other, and indicate the positions, approximately,on your orbit diagram.
19. Does the Moon rotate? If yes, how often? Suppose you lived on the Moon, in a base in the middle of the Moon's face as seen from here. How would the Sun move through your sky? How long between sunrise and sunset? How would the Earth move through your sky? Would the appearance of the Earth change, that is, would it have phases?
20. Explain with a diagram the orbit of Venus in Ptolemy's model. If Ptolemy had had a telescope, and could see the phases (shadowing) of Venus, would that have given him any doubts about his model? Explain why or why not.
21. Mars in its path through the sky sometimes loops backwards.
Explain in your own words why this happens
(a) using Ptolemy's model, and
(b) with our present day picture of the Solar System.
22. Here is a picture of a sundial:

The rod is parallel to the Earth's axis. Describe carefully how the movement of the Sun through the sky shows the time on this sundial -- in particular, it must read 12 one hour after it reads 11, right? Are you sure the sun's moving in the right direction for this thing to work?
23. As we went over in class, the chain of transmission of Greek knowledge ultimately to Europe has some surprising links.One was the Nestorians, declared heretic and kicked out of the Roman Empire, from their monastery at Edessa in present day Turkey (not the Edessa in Macedonia). They were welcomed by the Persians and set up shop at Gundishapur (or Jundishapur).Some were later given court appointments by the Arab Muslims in Baghdad. Use Google Earth to find out where these places are, put in place markers, and print off the image. Find the approximate distances from Edessa to Gundishapur to Baghdad, and state the approximate dates of these movements.
24. Recreate al-Khwarizmi's argument to solve x2 = 10x + 39, draw a diagram and explain your work.
(a)Standing on the beach, assume your eyes are 2 meters above sea level, and the sea is very calm. How far away is the horizon you see?
Hint: draw a circle, representing the surface of the curving earth, and your eyes are just above the circle -- now draw a line from your eyes to the furthest point visible on the circle. How does that line relate to the circle? Draw lines from your eye to the center of the earth, and from the furthest point you can see to the center of the earth. Take it from there...
How far away is it as seen from your hotel balcony, your eyes now being 18 meters above sea level?
(c) Suppose you watch the sunset, standing on the beach. As the last bit of the sun's disk just disappears, you race up to your room and look from the balcony. How fast did you have to get there to see any of the sun? (let's assume the hotel is on the equator.)
Hint: as the earth turns, seen from above the shadow line between night and day moves across the ground. How fast is it moving?
26. A simple sundial consists of a circular flat piece of white paper, and a vertical stick in the middle. Discuss the path traced by the shadow of the stick at four times in the year: the solstices and the equinoxes, do it for the equator and for the north pole.
27. Suppose you set up this sundial on the moon. What do you think the path of the shadow would be?
28. Look at this picture called Earthrise. How do you think the earth moves through the sky as seen from the moon?
HINT for the last two questions: http://nssdc.gsfc.nasa.gov/planetary/lunar/luna3_farside_big.gif is a picture of the far side of the moon, taken by a Russian spacecraft in 1959, and the first time anyone had seen that side.
29. There will be an eclipse of the Moon on the (look one up!), at full Moon. Could there ever be an eclipse of the Moon when the Moon is only half full? Show the Earth, Moon and Sun on a diagram to support your argument.
30. (a) Explain, with a diagram, what is meant by the "Ecliptic". What is the "Zodiac"?
(b) Find from a calendar the dates of the Winter Solstice, the Summer Solstice, the Spring Equinox and the Autumn Equinox. Draw a sketch of the Earth's path around the Sun, showing where it is on these four days, including an indication of the angle between the North Pole-South Pole axis and the direction to the Sun.
(c) Count the days exactly in the four quarters of the year between solstices and equinoxes. Are these periods all the same length? Would you expect them to be? Explain.
31. In November 2006, there was a transit of Mercury, meaning that the planet Mercury went directly between the Earth and the Sun, looking like a small black dot on the Sun's surface.The next transit will be in 2009, then ten years after that.
(a) Since Mercury goes once around every 88 days, and its orbit is between us and the sun, can you explain why these transits are so infrequent? (Hint: recall our discussion of why eclipses of the Moon are fairly rare).
(b) Transits of Mercury have been observed for centuries: they are always in May or November. Can you suggest an explanation? What's wrong with the other months?
32. Check your understanding of Archimedes' calculation of pi by finding what lower bound on the value of pi you can discover by inscribing first a square, then a regular octagon, in a circle.
Galileo
1. Why were Copernicus' ideas ultimately much more widely accepted than Aristarchus's very similar ideas?
2. Galileo's measurement of mountains on the Moon
Suppose that, when the moon is half full, a point of light can be seen in the dark half, a distance one-twentieth of the diameter of the moon away from the dark/light boundary. If it is a mountaintop, how high is the mountain?
3. Galileo showed off
his new telescope to the Doge from the Campanile in

Estimate the distance to the horizon as seen from the observation point on the Campanile.
(How to do this: first, come up with some reasonable estimate of the height (clearly not the full height of the Campanile). Next, draw a diagram of the Earth, with the campanile and the horizon showing. This should remind you of the diagram for problem #2 above!)
4. State in your own words Galileo's anti-Aristotle argument involving uniting two bodies having different "natural speeds".
5. The text below is a direct copy from Galileo's own introduction to his work on acceleration, one of the most important concepts in physics.Read it carefully, and then write an explanation in your own words, including drawing a graph of speed as a function of time for an object falling from rest.Note: for the word "momenta" he uses, you can just substitute "speed".
THEOREM I, PROPOSITION I
The time in which any space is traversed by a body starting from rest and uniformly accelerated is equal to the time in which that same space would be traversed by the same body moving at a uniform speed whose value is the mean of the highest speed and the speed just before acceleration began.
Let us represent by the line AB (see figure below) the time in which the space CD is traversed by a
body which starts from rest at C and is uniformly accelerated; let the final
and highest value of the speed gained during the interval AB be represented by
the line EB, drawn at right angles to AB; draw the line AE, then all lines
drawn from equidistant points on AB and parallel to BE will represent the
increasing values of the speed, beginning with the instant A. Let the point F
bisect the line EB; draw FG parallel to BA, and GA parallel to FB, thus forming
a parallelogram AGFB which will be equal in area to the triangle AEB, since the
side GF bisects the side AE at the point I; for if the parallel lines in the
triangle AEB are extended to GI, then the sum of all the parallels contained in
the quadrilateral is equal to the sum of those contained in the triangle AEB;
for those in the triangle IEF are equal to those contained in the triangle GIA,
while those included in the trapezium AIFB are common. Since each and every
instant of time in the time-interval AB has its corresponding point on the line
AB, from which points parallels drawn in and limited by the triangle AEB
represent the increasing values of the growing velocity, and since parallels
contained within the rectangle represent the values of a speed which is not
increasing, but constant, it appears, in like manner, that the momenta
[momenta] assumed by the moving body may also be represented, in the case of
the accelerated motion, by the increasing parallels of the triangle
 AEB,
and, in the case of the uniform motion, by the parallels of the rectangle GB.
For, what the momenta may lack in the first part of the accelerated motion (the
deficiency of the momenta being represented by the parallels of the triangle
AGI) is made up by the momenta represented by the parallels of the triangle
IEF.
AEB,
and, in the case of the uniform motion, by the parallels of the rectangle GB.
For, what the momenta may lack in the first part of the accelerated motion (the
deficiency of the momenta being represented by the parallels of the triangle
AGI) is made up by the momenta represented by the parallels of the triangle
IEF.
Hence it is clear that equal spaces will be traversed in equal times by two bodies, one of which, starting from rest, moves with a uniform acceleration, while the momentum of the other, moving with uniform speed, is one-half its maximum momentum under accelerated motion. Q.E.D.
6. Measure your reaction time using Galileo's concept of acceleration
If you hold a ruler against a wall, and let it fall, assuming it's not in contact with the wall, it will pick up speed at a rate of 10 meters per second per second.
(a) Write down how fast it's going after: 0.1 sec., 0.12 sec., 0.15 sec., 0.18 sec., 0.2 sec.
(b) Write down its average speed during the first 0.1 sec., the first 0.12 sec., ..., 0.2 sec.
(c) Work out how far it fell after 0.1 sec., 0.12 sec., 0.15 sec., 0.18 sec., 0.2 sec.
(d) Use these results to plot a graph of distance as a function of time from time 0 to time 0.2 sec.
(Guess the first 0.1 sec. -- remembering it always falls four times as far in twice the time!)
(e) Use your graph and a friend to find your reaction time, and state what it is. Have several tries and take the average.
7. Galileo's Analysis of Projectile Motion
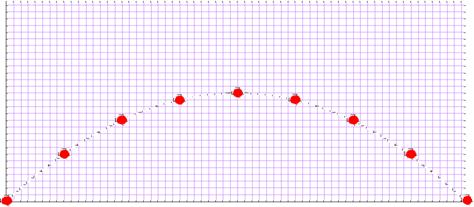
The above picture represents the flight of a ball thrown into the air (although air resistance effects have been neglected). The background grid is in one-foot squares. The blobs represent the position of the ball at successive quarter-second intervals.
(a) By counting lines, find the average horizontal velocity of the ball, in feet per second, during the first quarter of a second. (Remember, each square is one foot across (from side to side or top to bottom), and average speed = distance/time.)
(b) By reviewing the whole picture, find how the horizontal velocity (in feet per second) varies throughout the flight.
(c) By counting squares, find the average vertical velocity of the ball during the first quarter of a second.
(d) Make a table of the ball's average vertical velocity for all eight quarter-second periods in the flight. Count velocity upwards as positive, downwards as negative.
(e) Use your results from part (d) to plot a graph of the ball's vertical velocity (on the y-axis) as a function of time (on the x-axis) for the whole flight.
(f) Acceleration is rate of change of velocity. It is measured here in feet per second per second. Use your graph from (e) to plot a graph of the vertical acceleration as a function of time for the whole flight.
(g) What can you conclude about the acceleration of the ball at the topmost point of the path?
(h) Suppose now instead that the ball had been thrown directly upwards. Would it be accelerating at the topmost point of its flight?
(i) Galileo states in Two New Sciences (page 153): "..so far as I know, no one has yet pointed out that the distances traversed, during equal intervals of time, by a body falling from rest, stand to one another in the same ratio as the odd numbers beginning with unity". (The odd numbers beginning with unity just means 1, 3, 5, 7, ...). Show how you can verify this assertion using the picture above. What are the total distances fallen at the end of each quarter second starting from rest (at the top)?
8. Galileo's Scaling: an Example
In an experiment on scaling carried out in 1883, a dog of mass 3 kg. and surface area 2500 sq. cm. was found to need 300 calories a day to stay alive and warm (no exercise or weight change). Another dog of mass 30 kg. and surface area 10,000 sq. cm. was found to need 1100 calories a day.
(a) Do the calorie requirements correlate better with mass or surface area? Explain what you would expect. How precise would you expect the correlation to be?
(b) Make an estimate of your own mass and surface area, and, assuming you are doglike for purposes of this question, how many calories do you need a day to stay alive, without exercise and at constant weight?
Kepler's Laws
1. Use the Kepler's Laws applet to put a planet in an elliptical orbit.
(a) At the planet's nearest point to the sun, the speed reaches a maximum. Take two points close together on either side of this point, and draw the two velocity vectors for these points. By finding the change in velocity between the points, find the direction of the acceleration.
(b) Now do the same thing for the farthest point from the Sun. By watching the applet, how would you say the accelerations at these two points (nearest and farthest) compare?
(c) Now consider some point halfway or so between these points. Now speed as well as direction is changing! Try to see in what direction the acceleration is now.
2. (a) The satellites that transmit TV signals for home dish reception are all in what are called "geosynchronous" orbits, the satellites go once around the earth in 24 hours. Why were they placed in those particular orbits? In other words, how does that help reception of the TV signal?
(b) Use Kepler's Third Law and what you already know (or can look up) about the moon to predict the radius of the orbit of a geosynchronous satellite. Compare your result with the data given at the Kepler's Laws site, and explain any differences.
(c) To be precise, they actually go around once in 23 hours and 56 minutes. What's that about?
Newton and Newton's Laws
1. For Newton's cannon shooting at a low speed, it's clear that the cannonball follows the usual path, accelerating towards the ground. Explain in your own words how it can be that, at the right fast speed, shot above the atmosphere, the cannonball will stay at the same height, and never reach the ground.Make clear whether or not it is accelerating, and in what direction. (It might help to look at the applet).
2. State Newton's Second Law.
Suppose you are standing on a spring bathroom scale in an elevator which is at rest. What is your acceleration? What forces are acting on you? What is the reading on the bathroom scale?
Suppose now you push the button for a higher floor, and the elevator begins to move. After three seconds it is going up at a steady one meter per second. Did you accelerate? Are you still accelerating? How do you think the reading on the scale will vary as the elevator begins to move then settles to a steady speed? (Just answer qualitatively - no numbers expected.)
Now imagine disaster - the rope holding the elevator snaps,
there are no safety features, and the elevator plunges down the shaft in free
fall. You avail yourself of this golden opportunity to check
Read the second selection from Two New Sciences I've put on the Web until you find a sentence or two relevant to the above disaster scenario, and explain the connection.
3. If you are sitting at rest on a stool (so your legs are just hanging) what forces are acting on you? What are the corresponding Newtonian reaction forces to these forces, and what are they acting on?
4. A sky diver jumps out of a plane and is in free fall.Air resistance increases with speed, and her downward velocity approaches a limit of 80 meters per second (about 160 mph, terminal velocity). After falling at close to this speed for several seconds, she opens a parachute and her speed quickly drops to about 3 meters per second, and remains the same until she lands.
Plot a graph showing qualitatively her downward acceleration from the moment she leaves the plane until after she's landed on the ground. (Qualitatively means you should get the direction right, and some idea of where the acceleration is large, where it's very large, and where it's small).
State what forces were acting on her at each stage in the descent.
5.(a) The figure represents a pendulum (a bob-a small round weight, on a string) swinging back and forth, assume it is shown at the furthest point of its swing in each direction and in the middle of the swing. On the first set, show the velocity vector appropriate to these positions in the swing, on the lower set of pictures show the acceleration vectors for the three instants. Don't worry too much about representing the magnitudes, but think carefully about direction.
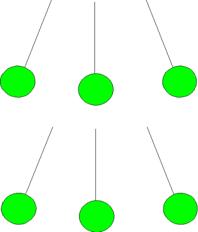
(b) Suppose the string is cut as the pendulum swings through the lowest point. Sketch the path of the pendulum from before the swing is cut until well after. How does the velocity of the pendulum the instant before the string is cut compare with that the instant after? How does the acceleration of the pendulum the instant before the string is cut compare with that the instant after?
(c) Now suppose instead the string is cut when the pendulum has reached its furthest point to the right in the swing. Sketch the path of the pendulum from before the string is cut until well after, and again compare the velocity and acceleration of the pendulum the instant before the string is cut with the instant after.
6.
Using Newton's Law of Gravitation to weigh the Sun and the Galaxy
We've weighed the earth, let's weigh the sun.
We know from Cavendish's experiment, and Newton's Universal Law of Gravitation, that the force of attraction between the earth and the sun is GMm/r2, where G is the gravitational constant, found by Cavendish to be 6.67 x 10-11, M is the mass of the sun, m the mass of the earth, and r the distance of the earth from the sun, which is 150,000,000 kilometers. (NOTE: in the formula for the force, r must be given in meters).
(This force causes the earth to accelerate towards the sun, that is, it deviates from straight line motion into a circle, just like Newton's cannonball. The strategy is to find how far it falls below a straight line in one second and figure out from that what its acceleration towards the sun must be. This acceleration is caused by the gravitational attraction force, which depends on the mass of the sun. Newton's Second Law gives the relation between the acceleration and the force, and enables us to find the mass of the sun.)
Using the fact that the earth goes around its orbit completely in one year, find how far the earth travels in one second. Now, find how far it "falls" below straight line motion in that one second. (HINT: call the distance it falls x, then write down Pythagoras' theorem for the usual triangle, and argue that x2 can be safely neglected. Then it's easy to find x.)
Since the time interval we are taking is just one second, the distance the earth falls below the straight line in that period must be equal to its average velocity in that direction (that is, towards the sun) during the one second. So what is the earth's velocity in that direction at the end of the one second period?
So what is its acceleration?
Write down Newton's Second Law for this acceleration, which is caused by the sun's gravitational attraction, and from it deduce the mass of the sun. Notice that you do not need to know the mass of the earth - why not?
7. The (almost) ultimate weighing job: estimating the mass of our galaxy.
The solar system is closer to the edge than the middle of our galaxy (the Milky Way), and is moving in an approximately circular path at about 250 kilometers per second. The radius of the circle -- the distance to the center of the galaxy -- is about 30,000 light years, where one light year is the distance light travels in one year.
Assume the solar system's circular motion about the center of the galaxy is caused by the gravitational attraction from the other stars in the galaxy. This attraction turns out to be not too different from what it would be if we lumped them all together in the middle in one huge mass M. Find this mass by the same method we used to find the earth's mass and the sun's mass, given G = 6.67 x 10-11.
Assuming the sun is a typical star, estimate how many stars there are in our galaxy.
(Footnote: it turns out that the gravitational attraction towards the center is greater than can be accounted for from the number of stars.There's something else there that we can't see! There is dark matter, and dark energy... . Nobody understands this very well.)
8. "When I throw a ball upwards, the force of my hand keeps it going for a while, but then that runs out, gravity takes over, and the ball begins to fall."
State in your own words what is wrong with the above statement.
Write a correct description of this sequence of events: in other words, from the instant your hand begins to move, until the ball is at rest on the ground, state what forces are acting on the ball, and qualitatively, what its acceleration is, during each part of the throw.
Reactions to Newton
1. A quote from the French poet Paul Valéry (1871-1945): "One had to be a Newton to notice that the moon is falling, when everyone sees that it doesn't fall".
Write a half-page or so explanation of this apparent paradox for a friend who knows very little science, including brief explanations of the relevant Newton's Laws.
2. (a) Find out what Thomas Jefferson thought of Isaac Newton, and write a couple of sentences or so summarizing TJ's opinion.
(b) Write a few sentences on how the Scientific Revolution (that is, mainly, the work of Galileo and Newton) influenced the Founding Fathers and hence the Declaration of Independence, etc., (if at all).
Einstein and Relativity
1. Draw a diagram showing the orbits of earth, Jupiter and Io and explain in your own words how Römer found the speed of light by observing eclipses of Io.
Reading Assignment:Read carefully lectures 18, 19, 20, 21, then answer the following:
2. Imagine you are in a ship with a silent engine sailing on a perfectly smooth sea, you are in a closed room with no window.
(a) How can you tell if the ship, moving in a straight line,
is slowing down? Draw a little diagram
of you sitting on a chair, with the forces on you, and ![]() .
.
(b) How can you tell if the ship, moving at constant speed, is moving in a circle? Draw a similar diagram.
(c) Now imagine you don't know the direction of the front of the ship -- you're just in a featureless cubical room, but you can have various physics-type toys. Do (a) and (b) feel different to you?. Could you distinguish between them somehow? (Hint: Foucault's Pendulum!)
3. If Galileo's experiment with the two guys with lanterns were reenacted with lasers, and one person is on the Moon, the other on Earth, do you think a good estimate of the speed of light could be made?
4. After reading lecture 21, explain how much a clock is slowed down as seen by you if it's moving relative to you at 80% of the speed of light, that is at 0.8c, where c = 3x108 meters per second. How long would it take a spaceship moving at that speed to reach alpha Centauri, 4 light years from here? How much would the astronauts age on the trip?
5. Explain in your own words the Fitzgerald contraction, and how it follows from the slowing down of a moving clock.