
Michael Fowler
University of Virginia
Index of Lectures and Overview of the Course
Link to Previous Lecture
Plato, with his belief that the world was constructed with geometric
simplicity and elegance, felt certain that the sun, moon and planets,
being made of aither, would have a natural circular motion, since
that is the simplest uniform motion that repeats itself endlessly,
as their motion did. However, although the "fixed stars"
did in fact move in simple circles about the North star, the sun,
moon and planets traced out much more complicated paths across
the sky. These paths had been followed closely and recorded since
early Babylonian civilization, so were very well known. Plato
suggested that perhaps these complicated paths were actually combinations
of simple circular motions, and challenged his Athenian colleagues
to prove it.
The first real progress on the problem was made by Eudoxus, at
Plato's academy. Eudoxus placed all the fixed stars on a huge
sphere, the earth itself a much smaller sphere fixed at the center.
The huge sphere rotated about the earth once every twenty-four
hours. So far, this is the standard "starry vault" picture.
Then Eudoxus assumed the sun to be attached to another sphere,
concentric with the fixed stars' sphere, that is, it was also
centered on the earth. This new sphere, lying entirely inside
the sphere carrying the fixed stars, had to be transparent, since
the fixed stars are very visible. The new sphere was attached
to the fixed stars' sphere so that it, too, went around every
twenty-four hours, but in addition it rotated slowly about
the two axis points where it was attached to the big sphere, and
this extra rotation was once a year. This meant that the sun,
viewed against the backdrop of the fixed stars, traced out a big
circular path which it covered in a year. This path is the ecliptic.
To get it all right, the ecliptic has to be tilted at 23½
degrees to the "equator" line of the fixed stars, taking
the North star as the "north pole".
This gives a pretty accurate representation of the sun's motion,
but it didn't quite account for all the known observations at
that time. For one thing, if the sun goes around the ecliptic
at an exactly uniform rate, the time intervals between the solstices
and the equinoxes will all be equal. In fact, they're not-so the
sun moves a little faster around some parts of its yearly journey
through the ecliptic than other parts. This, and other considerations,
led to the introduction of three more spheres to describe the
sun's motion. Of course, to actually show that the combination
of these motions gave an accurate representation of the sun's
observed motion required considerable geometric skill! Aristotle
wrote a summary of the "state of the art" in accounting
for all the observed planetary motions, and also those of the
sun and the moon. This required the introduction of fifty-five
concentric transparent spheres. Still, it did account for
everything observed in terms of simple circular motion, the only
kind of motion thought to be allowed for aither. Aristotle himself
believed the crystal spheres existed as physical entities, although
Eudoxus may have viewed them as simply a computational device.
It is interesting to note that, despite our earlier claim that
the Greeks "discovered nature", Plato believed the planets
to be animate beings. He argued that it was not possible that
they should accurately describe their orbits year after year if
they didn't know what they were doing-that is , if they had no
soul attached.
A little later, Eratosthenes and Aristarchus between them got
some idea of the size of the earth-sun-moon system, as we discusses
in an earlier lecture.
And, to quote from Archimedes (see Heath, Greek Astronomy),
"Aristarchus of Samos brought out a book consisting of
certain hypotheses, in which the premises lead to the conclusion
that the universe is many times greater than it is presently thought
to be. His hypotheses are that the fixed stars and the sun remain
motionless, that the earth revolves about the sun in the circumference
of a circle, the sun lying in the middle of the orbit, and that
the sphere of the fixed stars, situated about the same center
as the sun, is so great that the circular orbit of the earth is
as small as a point compared with that sphere."
The tiny size of the earth's orbit is necessary to understand
why the fixed stars do not move relative to each other as the
earth goes around its orbit.
Aristarchus' model was not accepted, nor even was the suggestion
that the earth rotates about its axis every twenty-four hours.
However, the model of the fifty-five crystal spheres was substantially improved on. It did have some obvious defects. For example, the sun, moon and planets necessarily each kept a constant distance from the earth, since each was attached to a sphere centered on the earth. Yet it was well-known that the apparent size of the moon varied about ten per cent or so, and the obvious explanation was that its distance from the earth must be varying. So how could it be attached to a sphere centered on the earth? The planets, too, especially Mars, varied considerably in brightness compared with the fixed stars, and again this suggested that the distance from the earth to Mars must vary in time.
A new way of combining circular motions to account for the movements
of the sun, moon and planets was introduced by Hipparchus (second
century BC) and realized fully by Ptolemy (around AD 150). Hipparchus
was aware the seasons weren't quite the same length, so he suggested
that the sun went around a circular path at uniform speed, but
that the earth wasn't in the center of the circle. Now the solstices
and equinoxes are determined by how the tilt of the earth's axis
lines up with the sun, so the directions of these places from
the earth are at right angles. If the circle is off center, though,
some of these seasons will be shorter than others. We know the
shortest season is fall (in our hemisphere).
Another way of using circular motions was provided by Hipparchus'
theory of the moon. This introduced the idea of the "epicycle",
a small circular motion riding around a big circular motion.
(See below for pictures of epicycles in the discussion of Ptolemy.)
The moon's position in the sky could be well represented by such
a model. In fact, so could all the planets. One problem was that
to figure out the planet's position in the sky, that is, the line
of sight from the earth, given its position on the cycle and on
the epicycle, needs trigonometry. Hipparchus developed trigonometry
to make these calculations possible.
Ptolemy wrote the "bible" of Greek (and other ancient)
astronomical observations in his immense book, the "Almagest".
This did for astronomy at the time what Euclid's Elements did
for geometry. It gave huge numbers of tables by which the positions
of planets, sun and moon could be accurately calculated for centuries
to come. We cannot here do justice to this magnificent work, but
I just want to mention one or two significant points which give
the general picture.
To illustrate the mechanism, we present here a slightly simplified version of his account of how the planets moved. The main idea was that each planet (and also, of course, the sun and moon) went around the earth in a cycle, a large circle centered at the center of the earth, but at the same time the planets were describing smaller circles, or epicycles, about the point that was describing the cycle. Mercury and Venus, as shown in the figure, had epicycles centered on the line from the earth to the sun. This picture does indeed represent fairly accurately their apparent motion in the sky---note that they always appear fairly close to the sun, and are not visible in the middle of the night.

The planets Mars, Jupiter and Saturn, on the other hand, can be seen through the night in some years. Their motion is analyzed in terms of cycles greater than the sun's, but with epicycles exactly equal to the sun's cycle, and with the planets at positions in their epicycles which correspond to the sun's position in its cycle---see the figure below.
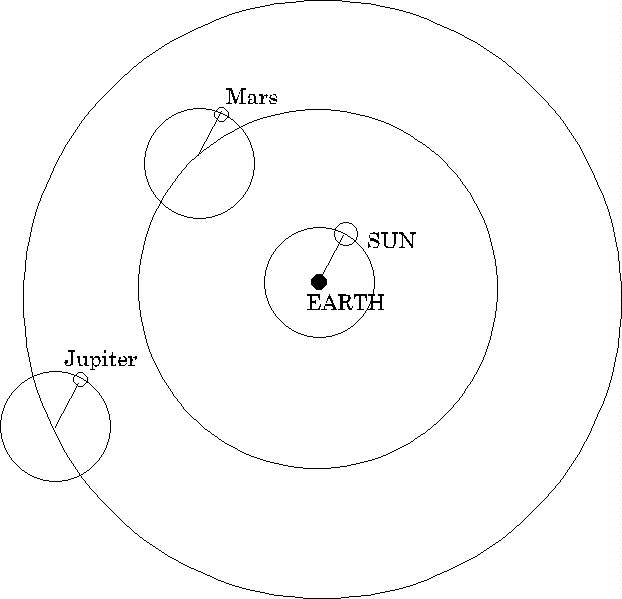
This system of cycles and epicycles was built up to give an accurate account of the observed motion of the planets. Actually, we have significantly simplified Ptolemy's picture. He caused some of the epicycles to be not quite centered on the cycles, they were termed eccentric. This departure from apparent perfection was necessary for full agreement with observations, and we shall return to it later. Ptolemy's book was called the Almagest in the Middle Ages, the Arabic prefix al with the Greek for "the greatest" the same as our prefix mega.
Ptolemy did, however, know that the earth was spherical. He pointed out that people living to the east saw the sun rise earlier, and how much earlier was proportional to how far east they were located. He also noted that, though all must see a lunar eclipse simultaneously, those to the east will see it as later, e.g. at 1 a.m., say, instead of midnight, local time. He also observed that on traveling to the north, Polaris rises in the sky, so this suggests the earth is curved in that direction too. Finally, on approaching a hilly island from far away on a calm sea, he noted that the island seemed to rise out of the sea. He attributed this phenomenon (correctly) to the curvature of the earth.
Copyright except where otherwise noted ©1995 Michael Fowler
Index of Lectures and Overview of the Course