previous index next

Galileo’s Acceleration Experiment

Michael Fowler, UVa Physics Department

Summarizing Aristotle’s View

Aristotle held that there are two kinds of motion for inanimate matter, natural and unnatural. Unnatural (or “violent”) motion is when something is being pushed, and in this case the speed of motion is proportional to the force of the push. (This was probably deduced from watching oxcarts and boats.) Natural motion is when something is seeking its natural place in the universe, such as a stone falling, or fire rising. (We are only talking here about substances composed of earth, water, air and fire, the “natural circular motion” of the planets, composed of aither, is considered separately).

For the natural motion of heavy objects falling to earth, Aristotle asserted that the speed of fall was proportional to the weight, and inversely proportional to the density of the medium the body was falling through. He did also mention that there was some acceleration, as the body approached more closely its own element, its weight increased and it speeded up. However, these remarks in Aristotle are very brief and vague, and certainly not quantitative.

Actually, these views of Aristotle did not go unchallenged even in ancient Athens. Thirty years or so after Aristotle’s death, Strato pointed out that a stone dropped from a greater height had a greater impact on the ground, suggesting that the stone picked up more speed as it fell from the greater height.

Two New Sciences

Galileo set out his ideas about falling bodies, and about projectiles in general, in a book called “Two New Sciences”. The two were the science of motion, which became the foundation-stone of physics, and the science of materials and construction, an important contribution to engineering.

The ideas are presented in lively fashion as a dialogue involving three characters, Salviati, Sagredo and Simplicio. The official Church point of view, that is, Aristotelianism, is put forward by the character called Simplicio, and usually demolished by the others. Galileo’s defense when accused of heresy in a similar book was that he was just setting out all points of view, but this is somewhat disingenuous---Simplicio is almost invariably portrayed as simpleminded.

For example, on TNS page 62, Salviati states:

I greatly doubt that Aristotle ever tested by experiment whether it be true that two stones, one weighing ten times as much as the other, if allowed to fall, at the same instant, from a height of, say, 100 cubits, would so differ in speed that when the heavier had reached the ground, the other would not have fallen more than 10 cubits.

Simplicio’s response to this is not to think in terms of doing the experiment himself to respond to Salviati’s challenge, but to scrutinize more closely the holy writ:

SIMP: His language would seem to indicate that he had tried the experiment, because he says: We see the heavier; now the word see shows he had made the experiment.

Sagredo then joins in:

SAGR: But I, Simplicio, who have made the test, can assure you that a cannon ball weighing one or two hundred pounds, or even more, will not reach the ground by as much as a span ahead of a musket ball weighing only half a pound, provided both are dropped from a height of 200 cubits.

This then marks the beginning of the modern era in science---the attitude that assertions about the physical world by authorities, no matter how wise or revered, stand or fall by experimental test. Legend has it that Galileo performed this particular experiment from the leaning tower of Pisa.

Galileo goes on to give a detailed analysis of falling bodies. He realizes that for extremely light objects, such as feathers, the air resistance becomes the dominant effect, whereas it makes only a tiny difference in the experiment outlined above.

Naturally Accelerated Motion

Having established experimentally that heavy objects fall at practically the same rate, Galileo went on to consider the central question about speed of fall barely touched on by Aristotle---how does the speed vary during the fall?

The problem is that it’s very difficult to answer this question by just watching something fall---it’s all over too fast. To make any kind of measurement of the speed, the motion must somehow be slowed down. Of course, some falling motions are naturally slow, such as a feather, or something not too heavy falling through water. Watching these motions, one sees that after being dropped the body rapidly gains a definite speed, then falls steadily at that speed. The mistake people had been making was in assuming that all falling bodies followed this same pattern, so that most of the fall was at a steady speed. Galileo argued that this point of view was false by echoing the forgotten words of Strato almost two thousand years earlier:

(TNS, page 163) But tell me, gentlemen, is it not true that if a block be allowed to fall upon a stake from a height of four cubits and drive it into the earth, say, four finger-breadths, that coming from a height of two cubits it will drive the stake a much less distance; and finally if the block be lifted only one finger-breadth how much more will it accomplish than if merely laid on top of the stake without percussion? Certainly very little. If it be lifted only the thickness of a leaf, the effect will be altogether imperceptible. And since the effect of the blow depends upon the velocity of this striking body, can any one doubt the motion is very slow .. whenever the effect is imperceptible?

Galileo’s Acceleration Hypothesis

Having established by the above arguments and experiments that a falling body continues to pick up speed, or accelerate, as it falls, Galileo suggested the simplest possible hypothesis (paraphrasing the discussion on TNS page 161):

A falling body accelerates uniformly: it picks up equal amounts of speed in equal time intervals, so that, if it falls from rest, it is moving twice as fast after two seconds as it was moving after one second, and moving three times as fast after three seconds as it was after one second.

This is an appealingly simple hypothesis, but not so easy for Galileo to check by experiment---how could he measure the speed of a falling stone twice during the fall and make the comparison?

Slowing Down the Motion

The trick is to slow down the motion somehow so that speeds can be measured, without at the same time altering the character of the motion. Galileo knew that dropping something through water that fell fairly gently did alter the character of the motion, it would land as gently on the bottom dropped from ten feet as it did from two feet, so slowing down the motion by dropping something through water changed things completely.

Galileo’s idea for slowing down the motion was to have a ball roll down a ramp rather than to fall vertically. He argued that the speed gained in rolling down a ramp of given height didn’t depend on the slope. His argument was based on an experiment with a pendulum and a nail, shown on page 171 of Two New Sciences. The pendulum consists of a thread and a lead bullet. It is drawn aside, the string taut, to some point C.

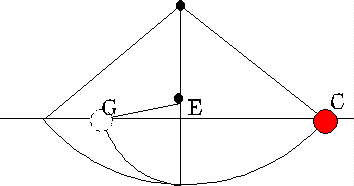
A nail is placed at E directly below the top end of the thread, so that as the pendulum swings through its lowest point, the thread hits the nail and the pendulum is effectively shortened, so that the bullet swings up more steeply, to G with the nail at E. Nevertheless, the pendulum will be seen to swing back up to almost the same height it started at, that is, the points G and C are the same height above level ground. Furthermore, when it swings back, it gets up as far as point C again, if we neglect a slight loss caused by air resistance. From this we can conclude that the speed with which the ball passes through the lowest point is the same in both directions. To see this, imagine first the situation without the nail at E. The ball would swing backwards and forwards in a symmetrical way, an ordinary pendulum, and certainly in this case the speed at the lowest point is the same for both directions (again ignoring gradual slowing down from air resistance). When we do put the nail in, though, we see from the experiment that on the swing back, the ball still manages to get to the beginning point C. We conclude that it must have been going the same speed as it swung back through the lowest point as when the nail wasn’t there, because the instant it leaves the nail on the return swing it is just an ordinary pendulum, and how far it swings out from the vertical depends on how fast it’s moving at the lowest point.

Galileo argues that a similar pattern will be observed if a ball rolls down a ramp which is smoothly connected to another steeper upward ramp, that is, the ball will roll up the second ramp to a level essentially equal to the level it started at, even though the two ramps have different slopes. It will then continue to roll backwards and forwards between the two ramps, eventually coming to rest because of friction, air resistance, etc.

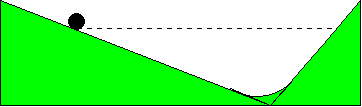
Thinking about this motion, it is clear that (ignoring the gradual slowing down on successive passes) it must be going the same speed coming off one ramp as it does coming off the other. Galileo then suggests we imagine the second ramp steeper and steeper---and we see that if it’s steep enough, we can think of the ball as just falling! He concludes that for a ball rolling down a ramp, the speed at various heights is the same as the speed the ball would have attained (much more quickly!) by just falling vertically from its starting point to that height. But if we make the ramp gentle enough, the motion will be slow enough to measure. (Actually, there is a difference between a rolling ball and a smoothly sliding or falling ball, but it does not affect the pattern of increase of speed, so we will not dwell on it here.)

Galileo’s Acceleration Experiment

We are now ready to consider Galileo’s experiment in which he tested his hypothesis about the way falling bodies gain speed. We quote the account from Two New Sciences, page 178:

A piece of wooden moulding or scantling, about 12 cubits long, half a cubit wide, and three finger-breadths thick, was taken; on its edge was cut a channel a little more than one finger in breadth; having made this groove very straight, smooth, and polished, and having lined it with parchment, also as smooth and polished as possible, we rolled along it a hard, smooth, and very round bronze ball. Having placed this board in a sloping position, by raising one end some one or two cubits above the other, we rolled the ball, as I was just saying, along the channel, noting, in a manner presently to be described, the time required to make the descent. We repeated this experiment more than once in order to measure the time with an accuracy such that the deviation between two observations never exceeded one-tenth of a pulse-beat. Having performed this operation and having assured ourselves of its reliability, we now rolled the ball only one-quarter the length of the channel; and having measured the time of its descent, we found it precisely one-half of the former. Next we tried other distances, compared the time for the whole length with that for the half, or with that for two-thirds, or three-fourths, or indeed for any fraction; in such experiments, repeated a full hundred times, we always found that the spaces traversed were to each other as the squares of the times, and this was true for all inclinations of the plane, i.e., of the channel, along which we rolled the ball. We also observed that the times of descent, for various inclinations of the plane, bore to one another precisely that ratio which, as we shall see later, the Author had predicted and demonstrated for them.

For the measurement of time, we employed a large vessel of water placed in an elevated position; to the bottom of this vessel was soldered a pipe of small diameter giving a thin jet of water which we collected in a small glass during the time of each descent, whether for the whole length of the channel or for part of its length; the water thus collected was weighed, after each descent, on a very accurate balance; the differences and ratios of these weights gave us the differences and ratios of the times, and this with such accuracy that although the operation was repeated many, many times, there was no appreciable discrepancy in the results.

Actually Doing the Experiment

We did the experiment in class in October 1996. O.K., we didn’t line the channel with parchment, and we used an ordinary large steel ball (about one inch in diameter). We did use a water clock, with a student letting a jet of water into a polystyrene(!) cup during the interval between another student releasing the ball at some distance up the ramp and it hitting the stop at the bottom. We performed the experiment three times for the full ramp, and three times for a quarter of the distance. We weighed the amount of water in the cup with an ordinary balance. We found, somewhat to our surprise, that the average amount for the full ramp was 56 grams, for the quarter ramp 28 grams. This was partly luck, there was a scatter of a few grams. However, it does suggest that Galileo was not exaggerating in his claims of accuracy in Two New Sciences, since he was far more careful than we were, and repeated the experiment many more times.

previous index next