previous
index
next
Naturally Accelerated Motion
Michael Fowler UVa Physics
Distance Covered in Uniform Acceleration
In the last lecture, we stated what we called Galileo’s acceleration hypothesis:
A falling body accelerates uniformly: it picks up equal amounts of speed
in equal time intervals, so that, if it falls from rest, it is moving twice as
fast after two seconds as it was moving after one second, and moving three
times as fast after three seconds as it was after one second.
We also found, from the experiment, that a falling body will fall four times
as far in twice the time. That is to say, we found that the time to roll
one-quarter of the way down the ramp was one-half the time to roll all the way
down.
Galileo asserted that the result of the rolling-down-the-ramp experiment
confirmed his claim that the acceleration was uniform. Let us now try to
understand why this is so. The simplest way to do this is to put in some
numbers. Let us assume, for argument’s sake, that the ramp is at a
convenient slope such that, after rolling down it for one second, the ball is
moving at two meters per second. This means that after two seconds it
would be moving at four meters per second, after three seconds at six meters
per second and so on until it hits the end of the ramp. (Note: to get an
intuitive feel for these speeds, one meter per second is 3.6 km/hr, or
2.25 mph.)
To get a clear idea of what’s happening, you should sketch a
graph of how speed increases with time. This is a straight line
graph, beginning at zero speed at zero time, then going through a point
corresponding to two meters per second at time one second, four at two seconds
and so on. It sounds trivial, but is surprisingly helpful to have this
graph in front of you as you read—so, find a piece of paper or an old
envelope (this doesn’t have to be too precise) and draw a line along the
bottom marked 0, 1, 2, for seconds of time, then a vertical line (or y-axis)
indicating speed at a given time—this could be marked 0, 2, 4, …
meters per second. Now, put in the points (0,0), (1,2) and so on, and
join them with a line.
From your graph, you can now read off its speed not just at 0, 1, 2 seconds,
but at, say 1.5 seconds or 1.9 seconds or any other time within the time
interval covered by the graph.
The hard part, though, is figuring out how far it moves in a given
time. This is the core of Galileo’s argument, and it is essential
that you understand it before going further, so read the next paragraphs
slowly and carefully!
Let us ask a specific question: how far does it get in two seconds?
If it were moving at a steady speed of four meters per second for two
seconds, it would of course move eight meters. But it can’t have
gotten that far after two seconds, because it just attained the speed of four
meters per second when the time reached two seconds, so it was going at slower
speeds up to that point. In fact, at the very beginning, it was moving
very slowly. Clearly, to figure out how far it travels during that
first two seconds what we must do is to find its average speed during
that period.
This is where the assumption of uniform acceleration comes in.
What it means is that the speed starts from zero at the beginning of the
period, increases at a constant rate, is two meters per second after one
second (half way through the period) and four meters per second after two
seconds, that is, at the end of the period we are considering. Notice
that the speed is one meter per second after half a second, and three meters
per second after one-and-a-half seconds. From the graph you should have
drawn above of the speed as it varies in time, it should be evident that, for
this uniformly accelerated motion, the average speed over this
two second interval is the speed reached at half-time, that is, two
meters per second.
Now, the distance covered in any time interval is equal to the average speed
multiplied by the time taken, so the distance traveled in two seconds is four
meters—that is, two meters per second for two seconds.
Now let us use the same argument to figure how far the ball rolls in just
one second. At the end of one second, it is moving at two meters per
second. At the beginning of the second, it was at rest. At the
half-second point, the ball was moving at one meter per second. By the
same arguments as used above, then, the average speed during the first second
was one meter per second. Therefore, the total distance rolled during the
first second is just one meter.
We can see from the above why, in uniform acceleration, the ball rolls four
times as far when the time interval doubles. If the
average speed were the same for the two second period as for the one
second period, the distance covered would double since the ball rolls
for twice as long a time. But since the speed is steadily increasing, the
average speed also doubles. It is the combination of these two
factors—moving at twice the average speed for twice the time—that
gives the factor of four in distance covered!
It is not too difficult to show using these same arguments that the
distances covered in 1, 2, 3, 4, ...seconds are proportional to 1, 4, 9, 16,
.., that is, the squares of the times involved. This is left as an
exercise for the reader.
A Video Test of Galileo’s Hypothesis
In fact, using a video camera, we can check the hypothesis of uniform
acceleration very directly on a falling object. We drop the ball beside a
meter stick with black and white stripes each ten centimeters wide, so that on
viewing the movie frame by frame, we can estimate where the ball is at each
frame. Furthermore, the camera has a built-in clock—it films at
thirty frames per second. Therefore, we can constantly monitor the speed
by measuring how many centimeters the ball drops from one frame to the next.
Since this measures distance traveled in one-thirtieth of a second, we must
multiply the distance dropped between frames by thirty to get the (average)
speed in that short time interval in centimeters per second.
By systematically going through all the frames showing the ball falling, and
finding the (average) speed for each time interval, we were able to draw a
graph of speed against time. It was a little rough, a result of our crude
measuring of distance, but it was clear that speed was increasing with time at
a steady rate, and in fact we could measure the rate by finding the speed
reached after, say half a second. We found that, approximately, the rate
of increase of speed was ten meters (1,000 cms) per second in each second of
fall, so after half a second it was moving at about five meters per second, and
after a quarter of a second it was going two and a half meters per second.
This rate of increase of speed is the same for all falling bodies,
neglecting the effect of air resistance (and buoyancy for extremely light
bodies such as balloons). It is called the acceleration due to gravity,
written g, and is actually close to 9.8 meters per second per second.
However, we shall take it to be 10 for convenience.
Throwing a Ball Upwards
To clarify ideas on the acceleration due to gravity, it is worth thinking
about throwing a ball vertically upwards. If we made another movie, we
would find that the motion going upwards is like a mirror image of that on the
way down—the distances traveled between frames on the way up get shorter
and shorter. In fact, the ball on its way up loses speed at a
steady rate, and the rate turns out to be ten meters per second per
second—the same as the rate of increase on the way down. For
example, if we throw the ball straight upwards at 20 meters per second (about 45
mph) after one second it will have slowed to 10 meters per second, and after
two seconds it will be at rest momentarily before beginning to come down.
After a total of four seconds, it will be back where it started.
An obvious question so: how high did it go? The way to approach this
is to find its average speed on the way up and multiply it by the time taken to
get up. As before, it is helpful to sketch a graph of how the speed is
varying with time. The speed at the initial time is 20 meters per second,
at one second it’s down to 10, then at two seconds it’s zero.
It is clear from the graph that the average speed on the way up is 10 meters
per second, and since it takes two seconds to get up, the total distance traveled
must be 20 meters.
Speed and Velocity
Let us now try to extend our speed plot to keep a record of the entire fall.
The speed drops to zero when the ball reaches the top, then begins to increase
again. We could represent this by a V-shaped curve, but it turns out to
be more natural to introduce the idea of velocity. Unfortunately velocity
and speed mean the same thing in ordinary usage, but in science velocity means
more: it includes speed and direction.
Our convention: velocity
upwards is positive, downwards is negative.
This is just a convention: it might sometimes be convenient to take
the opposite, with downward positive. The important thing is to have
opposite signs for the two opposite directions. You can see this is
useful if you’re trying to calculate distance covered by multiplying
together time and average velocity—if you traveled the same speed for
equal times in opposite directions, your average velocity was zero, and
you got nowhere. (In case you’re wondering how we deal with velocities
in several different directions, we’ll come to that soon. For now,
we’ll stick with up and down motion.)
If we plot the velocity of the ball at successive times, it is +20
initially, +10 after one second, 0 after two seconds, -10 after three seconds,
-20 after four seconds. If you plot this on a graph you will see that it
is all on the same straight line. Over each one-second interval, the
velocity decreases by ten meters per second throughout the flight. In
other words, the acceleration due to gravity is -10 meters per second per
second, or you could say it is 10 meters per second per second downwards.
What’s the Acceleration at the Topmost Point?
Most people on being asked that for the first time say zero. That’s
wrong. But to see why takes some very clear thinking about just what is
meant by velocity and acceleration. Recall Zeno claimed motion was
impossible because at each instant of time an object has to be in a particular
position, and since an interval of time is made up of instants, it could never
move. The catch is that a second of time cannot be built up of instants.
It can, however, be built up of intervals of time each as short as you
wish. Average velocity over an interval of time is defined by dividing
the distance moved in that interval by the time taken—the length of the
interval. We define velocity at an instant of time, such as the
velocity of the ball when the time is one second, by taking a small time
interval which includes the time one second, finding the average velocity over
that time interval, then repeating the process with smaller and smaller time
intervals to home in on the answer.
Now, to find acceleration at an instant of time we have to go through the
same process. Remember, acceleration is rate of change of velocity.
This means that acceleration, too, can be positive or negative! You might
think negative acceleration is just slowing down, but it could also mean
speeding up in the direction you’ve chosen for velocity to be
negative—so, be careful!
To find the acceleration at an instant we have to take some short but
non-zero time interval that includes the point in question and find how much
the velocity changes during that time interval. Then we divide that
velocity change by the time it took to find the acceleration, in, say, meters
per second per second.
The point is that at the topmost point of the throw, the ball does come to
rest for an instant. Before and after that instant, there is a brief
period where the velocity is so small it looks as if the ball is at rest.
Also, our eyes tend to lock on the ball, so there is an illusion that the ball
has zero velocity for a short but non-zero period of time. But this
isn’t the case. The ball’s velocity is always changing.
To find its acceleration at the topmost point, we have to find how its velocity
changes in a short time interval which includes that point. If we took,
for example, a period of one-thousandth of a second, we would find the velocity
to have changed by one centimeter per second. So the ball would fall one
two-thousandth of a centimeter during that first thousandth of a second from
rest-not too easy to see! The bottom line, though, is that the acceleration of
the ball is 10 meters per second per second downwards throughout the flight.
If you still find yourself thinking it’s got no acceleration at the
top, maybe you’re confusing velocity with acceleration. All these
words are used rather loosely in everyday life, but we are forced to give them
precise meanings to discuss motion unambiguously. In fact, lack of
clarity of definitions like this delayed understanding of these things for
centuries.
The Motion of Projectiles
We follow fairly closely here the discussion of Galileo in Two New Sciences,
Fourth Day, from page 244 to the middle
of page 257.
To analyze how projectiles move, Galileo describes two basic types of
motion:
(i) Naturally accelerated vertical motion, which is the motion of a
vertically falling body that we have already discussed in detail.
(ii) Uniform horizontal motion, which he defines as straight-line horizontal
motion which covers equal distances in equal times.
This uniform horizontal motion, then, is just the familiar one of an
automobile going at a steady speed on a straight freeway. Galileo puts it
as follows:
“Imagine any particle projected along a horizontal plane without
friction; then we know...that this particle will move along this same plane
with a motion that is uniform and perpetual, provided the plane has no
limits.”
This simple statement is in itself a substantial advance on Aristotle, who
thought that an inanimate object could only continue to move as long as it was
being pushed. Galileo realized the crucial role played by friction: if
there is no friction, he asserted, the motion will continue indefinitely.
Aristotle’s problem in this was that he observed friction-dominated
systems, like oxcarts, where motion stopped almost immediately when the ox
stopped pulling. Recall that Galileo, in the rolling a ball down a ramp
experiment, went to great pains to get the ramp very smooth, the ball very
round, hard and polished. He knew that only in this way could he get
reliable, reproducible results. At the same time, it must have been
evident to him that if the ramp were to be laid flat, the ball would roll from
one end to the other, after an initial push, with very little loss of speed.
Compound Motion
Galileo introduces projectile motion by imagining that a ball, rolling in uniform
horizontal motion across a smooth tabletop, flies off the edge of the table.
He asserts that when this happens, the particle’s horizontal motion will
continue at the same uniform rate, but, in addition, it will acquire a downward
vertical motion identical to that of any falling body. He refers to this
as a compound motion.
The simplest way to see what is going on is to study Galileo’s diagram
on page 249, which we reproduce here.
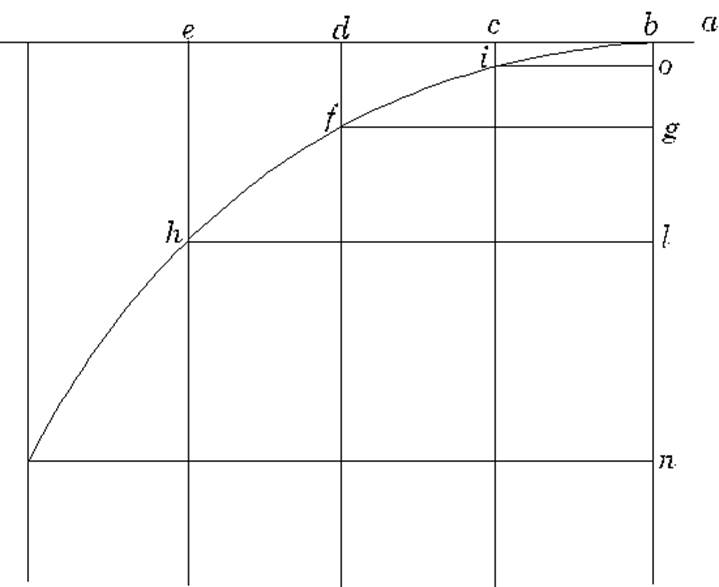
...and animate here!
Imagine the ball to have been rolling across a tabletop moving to the left,
passing the point a and then going off the edge at the point b.
Galileo’s figure shows its subsequent position at three equal time
intervals, say, 0.1 seconds, 0.2 seconds and 0.3 seconds after leaving the
table, when it will be at i, f, and h respectively.
The first point to notice is that the horizontal distance it has travelled
from the table increases uniformly with time: bd is just twice bc,
and so on. That is to say, its horizontal motion is just the same as if
it had stayed on the table.
The second point is that its vertical motion is identical to that of a
vertically falling body. In other words, if another ball had been dropped
vertically from b at the instant that our ball flew off the edge there,
they would always be at the same vertical height, so after 0.1 seconds when the
first ball reaches i, the dropped ball has fallen to o, and so on.
It also follows, since we know the falling body falls four times as far if the
time is doubled, that bg is four times bo, so for the projectile fd
is four times ic. This can be stated in a slightly different way,
which is the way Galileo formulated it to prove the curve was a parabola:
The ratio of the vertical distances dropped in two different times, for
example bg/bo, is always the square of the ratio of the
horizontal distances travelled in those times, in this case fg/io.
You can easily check that this is always true, from the rule of uniform
acceleration of a falling body. For example, bl is nine times bo,
and hl is three times io.
Galileo proved, with a virtuoso display of Greek geometry, that the fact
that the vertical drop was proportional to the square of the horizontal
distance meant that the trajectory was a parabola. His definition of a
parabola, the classic Greek definition, was that it was the intersection of a
cone with a plane parallel to one side of the cone. Starting from this
definition of a parabola, it takes quite a lot of work to establish that the
trajectory is parabolic. However, if we define a parabola as a curve of
the form y = Cx² then of course
we’ve proved it already!
previous
index
next
