previous
index
next
Galileo and the Telescope
Michael Fowler, UVa Physics
Copernicus Challenges Ptolemy’s Scheme
Ptolemy’s picture of the solar system was almost fully accepted for
the next fourteen hundred years, to be challenged by Copernicus (real name:
Nicolaus Koppernigk) a mathematician and astronomer with a Polish father and a
German mother, in 1530.
Copernicus’ picture of the solar system had the sun at the center, and
the earth went around it, as did the other planets.
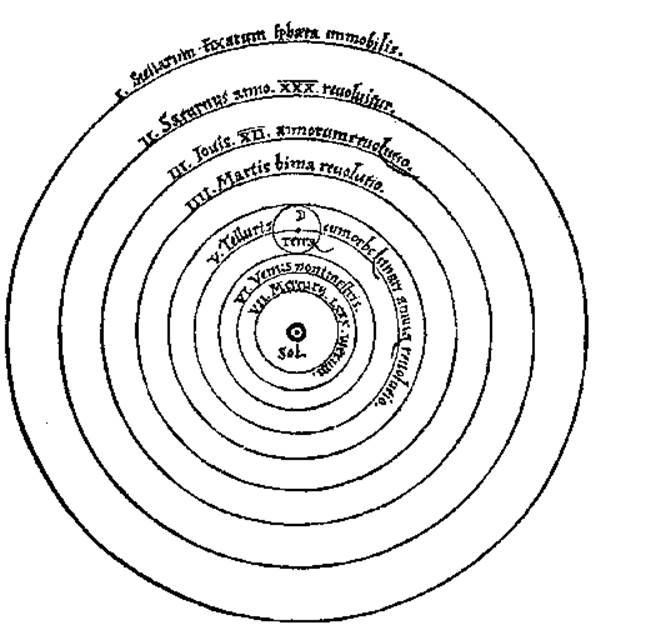
We show here the picture from his original publication. Notice that
the only exception to the rule that everything goes around the sun is the moon,
which continues to go around the earth. One objection to the picture was
that if the earth was indeed just another planet, how come it was the only one
with a moon?
Other objections were based on the Aristotelian point of view—it was
difficult to believe that all the other planets were composed of aither, and
the earth of the other four elements, if they were all behaving in so similar a
fashion. A further objection, which had long ago been raised by Aristotle
to the idea of a rotating earth, was that the stresses would cause it to fly
apart, and furthermore, anything thrown in the air would land far to the west.
Despite these problems, Pope Clement VII approved of a summary of Copernicus’
work in 1530, and asked for a copy of the full work when it was available.
This was not until 1543, the year Copernicus died.
As Copernicus’ new picture of the universe became more widely known,
misgivings arose. The universe had after all been created for mankind, so
why wasn’t mankind at the center? An intellectual revolutionary
called Giordano Bruno accepted Copernicus’ view, and went further,
claiming that the stars were spread through an infinite space, not just on an
outer sphere, and there were infinitely many inhabited worlds. Bruno was
burned at the stake in 1600.
The real breakthrough that ultimately led to the acceptance of Copernicus’
theory was due to Galileo, but was actually a technological rather than
a conceptual breakthrough. It was Galileo’s refinement and clever
use of the telescope that persuaded people that the moon was a lot like the
earth, and in some ways, so were the planets.
In fact, the Copernican heliocentric model had been suggested much earlier, by Aristarchus, as
discussed in an earlier lecture. But it was officially frowned upon, and not widely disseminated.
Copernicus actually mentioned Aristarchus in the first edition of his work, but dropped the reference in later versions.
Another quite likely connection is to earlier Islamic work. In accounting for differing planetary speeds at different orbital points, Copernicus replaced Ptolemy's equant explanation with epicycles that are essentially identical to al Tusi's couple,
even in notation. It's not clear how that idea might have been transmitted, but Copernicus was familiar with some Islamic work, and there were Jewish scholars
traveling widely in Europe and the east at that time. More details are available here.
The Evolution of the Telescope
(This section is mostly just a summary of Van Helden’s excellent
Introduction to Sidereus Nuncius, University of Chicago Press,
1989)
The first known use of a magnifying glass to aid in reading was in the
1200s, by Roger Bacon at Oxford. It proved a boon to aging scholars, many
of whom had been forced to retire while still relatively young. The idea
spread throughout Europe, and Italian craftsmen, were making glasses for old
men before 1300, (lens means lentil in Italian, so called because of the shape
of the pieces of glass used) and for the myopic young not until a hundred and
fifty years later. The reading glasses for the old men, who were
longsighted, were convex lenses, (bulging in the middle like () ),
whereas the glasses required by the shortsighted young were concave lenses,
thinner in the middle than at the edges like )( , and hence more difficult to
make and not so robust. The first time, as far as we know, that anyone
put two lenses together to make a telescope-like optical instrument was in
1608, in Holland. The inventor of an opera-glass like telescope was
called Lipperhey. He was unable to get a patent, however, because his
invention was deemed too easy to reproduce. Perhaps the reason it had not
been done before was that to get magnification, one needs a concave lens
stronger than the convex lens being used with it, and commonly the lenses in
wide use were the other way around.
Galileo found out about this invention in the spring of 1609, and
immediately set about improving it. He saw it as a possible way out of
his financial difficulties. He was an oldest son, and so was responsible
for his younger sisters’ dowries. He also had three children of his
own, by his mistress. At the time, he was a Professor of Mathematics in
the University of Padua, in the Venetian Republic. He soon put together a
spyglass with a magnification of three, which many other people had already
done. Galileo was an excellent experimentalist, and working with
different lenses, he realized that the magnification was proportional to the
ratio of the power of the concave (eyepiece) lens to the convex (more distant)
lens. In other words, to get high magnification he needed a weak convex
lens and a strong concave lens. the problem was that the opticians only
made glasses in a narrow range of strengths, and three or so was the best
magnification available with off the shelf lenses. Galileo therefore
learned to grind his own lenses, and by August, he had achieved about ninefold
linear magnification. This was an enormous improvement over everything
else on the market. Galileo therefore approached the Senate of Venice to
demonstrate his instrument. Many senators climbed the highest belltowers
in Venice to look through the glass at ships far out at sea, and were impressed
by the obvious military potential of the invention.
Galileo then wrote a letter to the Doge:
Galileo Galilei, a most humble servant of Your Serene Highness, being
diligently attentive, with all his spirit, not only to discharging the duties
pertaining to the lecturing of mathematics at the University of Padua, but also
to bringing extraordinary benefit to Your Serene Highness with some useful and
remarkable invention, now appear before You with a new contrivance of glasses,
drawn from the most recondite speculations of perspective, which render visible
objects so close to the eye and represent them so distinctly that those that
are distant, for example, nine miles appear as though they were only one mile
distant. This is a thing of inestimable benefit for all transactions and
undertakings, maritime or terrestrial, allowing us at sea to discover at a much
greater distance than usual the hulls and sails of the enemy, so that for two
hours or more we can detect him before he detects us...
Galileo concludes the letter by asking for tenure:
....(the telescope is) one of the fruits of the science which he has
professed for the past 17 years at the University of Padua, with the hope of
carrying on his work in order to present You greater ones, if it shall please
the Good Lord and Your Serene Highness that he, according to his desire, will
pass the rest of his life in Your service.
It is nice to report that Galileo was granted tenure, and a reasonable
salary, but—the bad news—with a proviso that further raises would
not be forthcoming.
Mountains on the Moon
Galileo’s first major astronomical discovery with the telescope was
that the Moon’s surface is mountainous, and not a perfect sphere as had
always been assumed (see his drawings in Sidereus Nuncius). He
built a convincing case for the reality of the mountains by sketching the
appearance of parts of the Moon’s surface at different times of the
month, that is, under different angles of lighting, and showing how the light
and shadow seen could be simply and naturally accounted for topographically,
rendering the prevailing theory at the time, that the variations in light arose
from something inside a perfect sphere, a cumbersome and unappealing
alternative. This caused an uproar.

From the National Central Library of Florence (BNCF).
He was able to estimate the height of the mountains on the moon by
seeing how far into the dark part bright spots could be discerned.
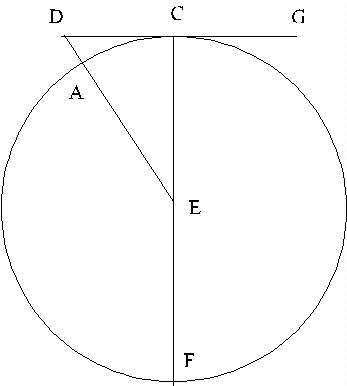
At half moon, a little geometry is enough to calculate the heights! Galileo
himself worked an example: suppose a bright spot, presumably an illuminated
mountaintop, is visible one-twentieth of a moon diameter into the dark side, at
half-moon. Then the picture is as shown here (and is taken from Sidereus
Nuncius). The light from the sun fully illuminates the right-hand
half of the moon, plus, for example, the mountaintop at D. (GCD is a ray
from the sun.) If the base of the mountain, vertically below D, is at A, and E
is the moon’s center, this is exactly the same problem as how far away is
the horizon, for a person of given height on a flat beach. It can be
solved using Pythagoras’ theorem as we did for that problem, with the
center of the moon E one of the points in the triangle, that is, the triangle
is EDC.
A problem with asserting the existence of mountains is the apparent smooth
roundness of the edge of the Moon, for which Galileo had two arguments. First,
ranges behind those on the edge would tend to fill in the gaps. This is
correct. Second, maybe things were fuzzed out by the Moon’s
atmosphere. This is wrong.
Galileo’s next major discovery began with his observation on January
7, 1610, of what he took to be a rather odd set of three small fixed stars near
Jupiter, and, in fact, collinear with the planet. These stars were
invisible to the naked eye. He looked again at Jupiter on successive
nights, and by the 15th had realized that he was looking at moons
of Jupiter, which were going around the planet with periods of the order of
days. This caused even more consternation than the demystification of the
Moon. Seven was a sacred number, and there were seven planets, wanderers,
or moving stars. Jupiter’s moons spoiled this. Furthermore,
they suggested that it was o.k. to go in a circle about something other
than the center of the universe, i.e. the Earth. This made
Copernicus’ argument, that the Moon goes around the Earth and the Earth
around the Sun, more plausible.
Again, Galileo’s grantsmanship is admirable. In a masterstroke
of public relations, he named the satellites after the Medici family, Dukes of
Tuscany, where he applied for the position of mathematician to the court.
He sent his most recent 20X telescope to the Duke, so that he could peruse the
stars named after him and his brothers, and emphasized its military
applicability.
previous
index
next


