previous index next
Basic Ideas in Greek Mathematics
Michael Fowler UVa Physics Department
Closing in on the Square Root of 2
In our earlier discussion of the irrationality of the square root of 2, we
presented a list of squares of the first 17 integers, and remarked that there
were several “near misses” to solutions of the equation m2
= 2n2. Specifically, 32 = 2×22 +
1, 72 = 2×52 - 1, 172 = 2×122
+ 1. These results were also noted by the Greeks, and set down in tabular form
as follows:
3 2
7 5
17 12
.
After staring at this pattern of numbers for a while, the pattern emerges: 3
+ 2 = 5 and 7 + 5 = 12, so the number in the right-hand column, after the first
row, is the sum of the two numbers in the row above. Furthermore, 2 + 5 = 7 and
5 + 12 = 17, so the number in the left-hand column is the sum of the number to
its right and the number immediately above that one.
The question is: does this pattern continue? To find out, we use it to find
the next pair. The right hand number should be 17 + 12 = 29, the left-hand 29 +
12 = 41. Now 412 = 1681, and 292 = 841, so 412
= 2× 292 - 1. Repeating the process gives 41 + 29 = 70 and 70
+ 29 = 99. It is easy to check that 992 = 2×702 +
1. So 992/702 = 2 + 1/702. In other words, the
difference between the square root of 2 and the rational number 99/70 is
approximately of the magnitude 1/702. (You can check this with your
calculator).
The complete pattern is now evident. The recipe for the numbers is given
above, and the +1’s and -1’s alternate on the right hand side. In
fact, the Greeks managed to prove (it can be done with elementary algebra) that
pairs of numbers can be added indefinitely, and their ratio gives a better and
better approximation to the square root of 2.
The essential discovery here is that, although it is established that the
square root of 2 is not a rational number, we can by the recipe find a rational
number as close as you like to the square root of two. This is sometimes
expressed as “there are rational numbers infinitely close to the square
root of 2” but that’s not really a helpful way of putting it. It’s
better to think of a sort of game - you name a small number, say, one
millionth, and I can find a rational number (using the table above and finding
the next few sets of numbers) which is within one millionth of the square root
of 2. However small a number you name, I can use the recipe above to find a
rational that close to the square root of 2. Of course, it may take a lifetime,
but the method is clear!
Zeno’s Paradoxes
Zeno of Elea (495-435 BC) is said to have been a self-taught country boy. He
was a friend of a well-known philosopher, Parmenides, and visited Athens with him, where he perplexed Socrates, among others, with a set of paradoxes.
(Plato gives an account of this in Parmenides.) We shall look at two of
them here.
Achilles and the Tortoise.
A two hundred yard race is set up between Achilles, who can run at 10 yards
per second, and the tortoise, who can run at one yard per second (perhaps
rather fast for a tortoise, but I’m trying to keep the numbers simple).
To give the tortoise a chance, he is given a one-hundred yard start.
Now, when Achilles has covered that first 100 yards, to get to where the
tortoise was, the tortoise is 10 yards ahead.
When Achilles has covered that 10 yards, the tortoise is 1 yard ahead.
When Achilles has covered that 1 yard, the tortoise is 1/10 yard ahead.
Now, Zeno says, there is no end to this sequence! We can go on forever
dividing by 10! So, Zeno concludes, Achilles has to cover an infinite number of
smaller and smaller intervals before he catches the tortoise. But to do an
infinite number of things takes an infinitely long time - so he’ll never
catch up.
What is wrong with this argument? Try to think it through before you read
on!
The essential point becomes clearer if you figure out how long it takes
Achilles to cover the sequence of smaller and smaller intervals. He takes 10
seconds to cover the first 100 yards, 1 second to cover the next 10 yards, 1/10
second for the next yard, 1/100 second for the next 1/10 of a yard, and so on.
If we write down running totals of time elapsed to each of these points we get
10 seconds, 11 seconds, 11.1 seconds, 11.11 seconds and so on. It is apparent
that the total time elapsed for all the infinite number of
smaller and smaller intervals is going to be 11.1111111…, with the 1’s
going on forever. But this recurring decimal, 0.111111… is just 1/9, as
you can easily check.
The essential point is that it is possible to add together an infinite
number of time intervals and still get a finite result. That means
there is a definite time-11 1/9 seconds-at which Achilles catches up
with the tortoise, and after that instant, he’s passed the tortoise.
The Arrow
Consider the flight of an arrow through the air. Let us divide time up into
instants, where an instant is an indivisibly small time. Now, during an
instant, the arrow can’t move at all, because if it did, we could divide
up the instant using the changing position of the arrow to indicate which bit
of the instant we are in.
However, a finite length of time-like a second-is made up of instants.
Therefore, if the arrow doesn’t move at all during an instant, it doesn’t
move in a sum of instants. Hence, it can’t move in one second!
What’s wrong with this argument?
Now there certainly is such a thing as an instant of time: for
example, if the arrow is in the air from time zero to time two seconds, say,
then there is one instant at which it has been in the air for exactly one
second.
The catch is, there is no way to divide time up into such instants.
Imagine the time from zero to two seconds represented by a geometric line two
inches long on a piece of paper. By geometric, I mean an ideal line, not one
that’s really a collection of microscopic bits of pencil lead, but a true
continuous line of the kind the Greeks imagined. Time has that kind of
continuity-there aren’t little gaps in time (at least, none we’ve
found so far). Now try to imagine the line made up of instants. You could start
by putting dots every millionth of a second, say. But then you could imagine
putting a million dots between each of those pairs of dots, to have a dot every
trillionth of a second. And why stop there? You could keep on indefinitely with
this division. But if you spend the rest of your life on this mental exercise,
you will never put a dot at the instant corresponding to the time being the
square root of two! And it has been proved by the mathematicians that there are
infinitely more irrational numbers than there are rational numbers.
So there really is no way to divide time up into instants. If you’re
still not sure, think about the following problem: what’s the next
instant after the instant at time equals one second?
Instants and Intervals
On the other hand, it is obviously useful in analyzing the motion of the
arrow to look at the motion one bit at a time-in other words, to divide the
time up somehow, to get a grip on how the arrow’s speed may be varying
throughout the flight. So how should we proceed? Zeno’s dividing of time
into instants was not very easy to understand, as we’ve seen. It’s
much easier to visualize dividing time into intervals. For example, the
two seconds the arrow is in the air could be divided into two hundred
intervals, each of length one-hundredth of a second. Then we could find its
average speed in each of those intervals by measuring how far it went in the
one-hundredth of a second, and multiplying by one hundred. That is, if it went
two feet in the one-hundredth of a second interval, it was traveling at two
hundred feet per second during that interval. (Of course, it might not be going
at that speed for the whole flight-that’s why we’ve divided it into
intervals, so that we can monitor the speed the whole time). Of course, if the
arrow hits something, it will slow down very rapidly-there will be a big change
in speed in one hundredth of a second. If we want to describe the motion of the
arrow in this situation, we must divide time up into smaller intervals, say
thousandths of a second, or even ten-thousandths of a second, depending on how
precisely we want to follow the change in speed.
Speed at an Instant
There is still a problem here we haven’t quite faced. All this
dividing time up into small intervals and finding the average speed in each
interval gives a pretty good idea of the arrow’s progress, but it’s
still a reasonable question to ask: just what is the arrow’s speed at
the instant one second after the flight began?
How do we answer that question? Think about it before you read on.
The essential point about speed is that it is a rate of change of
position-this is obvious when you think about measuring speed, it’s in
units like miles per hour, feet per second, etc. This implies that to make any
statement about speed we have to say how far the arrow moved between two
specified times. Therefore, to find the speed at the time one second after
takeoff, we would need to find where the arrow is at, say, 0.995 seconds after
takeoff, then at 1.005 seconds after takeoff. I’ve chosen here two times
that are one-hundredth of a second apart. If the arrow moves one and a half
feet during that period, it’s going at 150 feet per second.
You might object, though, that this is still not very precise. Probably 150
feet per second is pretty close to the arrow’s speed at one second after
takeoff, but it’s really an average over a time interval of one-hundredth
of a second, so may not be exactly the speed in the middle of the time.
This is true-it may not be. What we must do, at least in principle, is to take
a smaller time interval, say one-millionth of a second, again centered at time
one second, as before. We now measure how far the arrow moves in the
one-millionth of a second, and multiply that distance by one million to get the
arrow’s average speed over that very short time.
Of course, you could say you’re still not satisfied. You want to know
the precise speed at the one second mark, not some approximation based
on the average over a time interval. But, as we’ve just said, all speed
measurements necessarily involve some time interval, which, however, can be as
short as we like. This suggests how we should define what we mean by the speed
at one instant of time-we take a sequence of shorter and shorter time
intervals, each one centered at the time in question, and find the average
speed in each. This series of speed measurements will close in on the exact
speed at the time one second.
This should remind you of the discussion of the square root of two. There we
had a sequence of rational numbers such that if you come up with some small
number such as a millionth of a trillionth, we could always find a rational
within that distance of root two. Here we are saying that if you want the speed
to some preassigned accuracy, we can find it by taking a sufficiently small
time interval around the time in question, and computing the average speed in
that interval.
Actually, this may not be as difficult as it sounds. For example, imagine an
arrow moving far out in space at a steady speed, with no air resistance or
gravity to contend with. Then it will go at a steady speed, and the average
speed over all time intervals will be the same. This means we can find (in
principle) the exact speed at any given time without having to worry
about indefinitely small time intervals. Another fairly simple case is an arrow
gaining speed at a steady rate. Its speed in the middle of a time
interval turns out to be exactly equal to its average speed in the
interval. We shall be discussing this case further when we get to Galileo.
The Beginning of Calculus
We should emphasize that the above discussion of intervals, instants and so
on was not the response of the Athenians to Zeno. Only with later work by
Eudoxus, Euclid and Archimedes did the way to deal with these small quantities
gradually become apparent. Zeno’s contribution was that he initiated the
discussion that ultimately led to the calculus. In fact, according to Bertrand
Russell (History of Western Philosophy) Zeno taught Socrates the
Socratic method-the method of seeking knowledge by systematic question and
answer. Unhappily, Zeno’s approach did not win him powerful friends, and “he
finally lost his head for treason or something of the sort” (Bell,
Men of Mathematics).
Archimedes Begins Calculating Pi
Both the Babylonians and the Egyptians used approximations to pi, the ratio
of the circumference of a circle to its diameter. The Egyptians used a value
3.16, within one per cent of the true value. (Further details can be found in
Neugebauer, The Exact Sciences in Antiquity, Dover, page 78.) Actually,
this value follows from their rule for the area of a circle, (8/9.d)2,
but it is reasonable to suppose they could have constructed a circle and
measured the circumference to this accuracy. There are no indications that they
tried to calculate pi, using geometric arguments as Archimedes did.
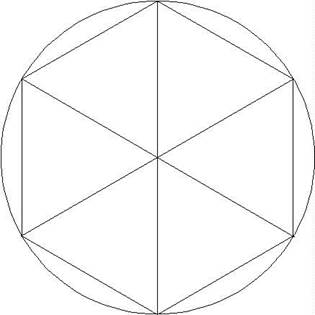
Following Archimedes, we first draw a circle of radius equal to one (so the diameter
is 2), and inscribe in it a regular (that is, all sides of equal length)
hexagon. It is evident that the hexagon is made up of six equilateral
triangles, since the 360 degree angle at the center of the circle is equally
divided into six, and the angles of a triangle add to 180 degrees. Therefore,
each side of each triangle is equal to the radius of the circle, that is, equal
to one. Thus the perimeter of the hexagon is exactly 6. It is clear from the
figure that the circumference of the circle, the total distance around, is
greater than the perimeter of the hexagon, because the hexagon can be seen as a
series of shortcuts on going around the circle. We conclude that pi, the ratio
of the circumference of the circle to its diameter, is greater than 3, but not
much-the hexagon looks quite close. (For example, much closer than, going
around a square boxed around the circle, which would be a distance of 8 radii.
If we approximated the circumference of the circle by this square, we would
guess pi = 4.)
So the first step-comparing the circle with the hexagon-tells us that pi is
greater than three. Archimedes’ next move was to find a polygon inscribed
in the circle that was closer to the circle than the hexagon, so that its
perimeter would be closer to the circumference of the circle. His strategy was
to double the number of sides of the polygon, that is, to replace the hexagon
by a twelve-sided regular polygon, a dodecagon. Obviously, from the figure, the
perimeter of the dodecagon is much closer to that of the circle than the
hexagon was (but it’s still obviously less, since, like the hexagon, it
is a series of shortcuts on going around the circle).
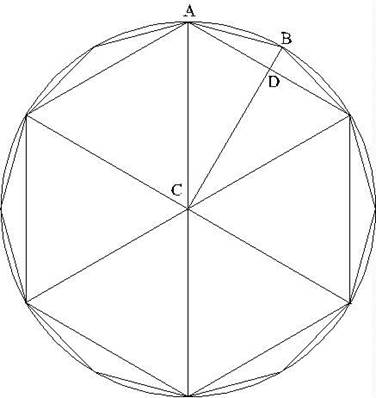
Calculating the perimeter of the dodecagon is not as simple as it was for
the hexagon, but all it require is Pythagoras’ theorem. Look at the
figure. We need to find the length of one side, like AB, and multiply it by 12
to get the total perimeter. AB is the hypotenuse of the right-angled triangle
ABD. We know the length AD is just ½ (recall the radius of the circle =
1). We don’t know the other length, BD, but we do know that BC must equal
1, because it’s just the radius of the circle again. Switching our
attention to the right-angled triangle ACD, we see its hypotenuse equals 1, and
one side (AD) equals ½. So from Pythagoras, the square of CD
must be ¾. We will write CD = ½×sqrt3.
Having found CD, we can find DB since CD + DB = CB = 1, that is, DB = 1 -
½×sqrt3. So we know the two shorter sides of the right-angled
triangle ADB, and we can find the hypotenuse using Pythagoras again.
The dodecagon turns out to have a perimeter 6.21, giving pi greater than
3.1. This is not quite as close as the Egyptians, but Archimedes didn’t
stop here. He next went to a 24-sided regular polygon inscribed in the circle.
Again, he just needed to apply Pythagoras’ theorem twice, exactly as in
the preceding step. The perimeter of the 24-sided regular polygon turns out to
be 6.26, giving pi greater than 3.13. (We are giving a slightly sloppy version
of his work: he always worked with rationals, and where the square root of 3
came in, he used 265/153 < sqrt3 < 1351/780. These limits came from an
algorithm originating with the Babylonians.)
In fact, Archimedes went on as far as the 96-sided regular polygon inscribed
in the circle. He then started all over again with regular polygons
circumscribed about the circle, so that the circle is touching the
middle of each side of the polygon, and is completely contained by it. Such a
polygon clearly has a perimeter greater than that of the circle, but
getting closer to it as we consider polygons with more and more sides.
Archimedes considered such a polygon with 96 sides.
So, with a series of polygons inside the circle, and another series outside
it, he managed to bracket the length of the circumference between two sets of
numbers which gradually approached each other. This is again reminiscent of the
Greek strategy in approximating the square root of 2. The result of all his
efforts was the inequality: 3 10/71 < pi < 3 1/7. If we take the average
of these two numbers, we find 3.14185. The correct value is 3.14159… .
Squaring the Circle
This phrase refers to the famous problem of finding an area with
straight-line boundaries equal in area to a circle of given diameter.
Archimedes proved that the area of a circle is equal to that of a right-angled
triangle having the two shorter sides equal to the radius of the circle and its
circumference respectively.
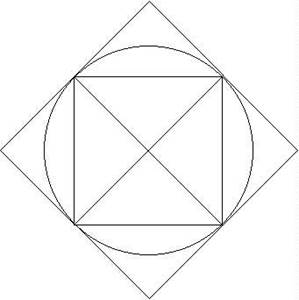
The idea of his proof is as follows. Consider first a square
inscribed in the circle. The square is made up of four triangles, each of
height h, say, and base length b. (Actually, b = 2h,
but we’ll keep them separate.)
The total area of the square is equal to
the total area of the 4 triangles, which is 4 times ½×h×b,
or ½×h×4b. Notice that this is the area of
a long thin triangle, with height equal to the distance h
from the middle of the side of the square to the center of the circle, and
base equal to the perimeter length 4b of the square.
The area of the square isn’t a very good approximation to that of the
circle, but we can improve it by replacing the square by a regular octagon,
with all its points on the circle. Now, this octagon can by divided into eight
triangles, following the same procedure as for the square. The height of each
of these triangles equals the distance from the center of the circle to the
middle of one side of the octagon. Just as for the square case, the total area
of these eight triangles is equal to that of a long thin triangle of the same
height, and with base length equal to the perimeter of the octagon.
It is evident that the height of the octagon’s triangles is closer to
the radius of the circle than the height of the square’s triangles, and
the perimeter of the octagon is closer to the circumference of the circle than
the perimeter of the square was.
The process is repeated: the octagon is replaced by a regular 16-sided
polygon, with all its points on the circle. This polygon is equal in area to
the sum of the 16 triangles formed by drawing lines from the center of the
circle to its points. These triangles all have the same height, so they have
total area the same as a long thin triangle having the same height, and base
length equal to the perimeter of the 16-sided polygon.
At this point, the pattern should be clear-as we go to polygons of 32, 64,
… sides, the total area of the polygon is the same as that of a right
angled triangle with a long side equal to the perimeter of the polygon, which
approaches the circumference of the circle as the polygons have more and more
sides, and the height of the triangle approaches the radius of the circle.
Therefore, the area of the polygons approaches ½×base×height
= ½×2×pi×r×r = pi×r2.
Eudoxus’ Method of Exhaustion
This section and the next are optional—they won’t
appear on any tests, etc. I just put them in for completeness.
In fact, the account given above doesn’t do justice to the tightness
of the Greeks’ geometric arguments. The approach to the limit of more and
more sided polygons approximating the circle better and better is a bit vague.
It’s not very clear how quickly this is happening.
Eudoxus clarified the situation by giving a procedure putting a lower limit
on how much more of the circle’s total area was covered by the new
polygon created at each step. Let’s begin with the square. In the figure,
we show the inscribed square EFGH, and also a circumscribed square ABCD.
Clearly, the area of square EFGH is exactly half of that of square ABCD. Since
the circle lies entirely inside ABCD, it follows that EFGH covers more than
half of the area of the circle.
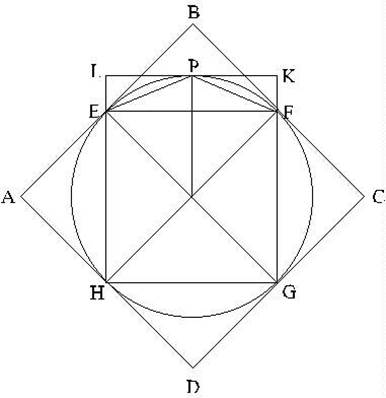
Now consider how much more of the circle’s total area is covered when
we go from the square to the octagon. We add triangular areas like EPF to each
side of the square. Now, notice that the triangle EPF has area exactly half of
the rectangular area ELKF. If we had added rectangular areas like that to the
four sides of the square, the circle’s area would have been completely
contained. This implies that by adding just the triangles, that is, going from
the square to the octagon, we are covering more than half of the area of the
circle that lay outside the square.
This same argument works at each step: so, the inscribed square covers more
than half the circle’s area, going to the octagon covers more than half
the rest, so the octagon covers more than three-quarters of the circle’s
area, the 16-sided inscribed polygon covers more than seven-eighths of the
circle’s area, and so on.
Archimedes used Eudoxus’ approach to prove that the area of a circle
was equal to that of the right-angled triangle with shorter sides equal to the
radius and the circumference of the circle. Suppose, he said, that the triangle’s
area is less than the circle’s. Then in the sequence of polygons with 4,
8, 16, 32, … sides, we will get to one with area greater than the
triangle’s. But that polygon will have an area equal to that of a number
of triangles equal to its number of sides, and, as we’ve argued above,
the sum of their areas is equal to that of a triangle having their height and
base length equal to the perimeter of the polygon. But their height is less
than the radius of the circle, and the perimeter is less than the circumference
of the circle. Hence their total area must be less that that of the triangle
having height the radius of the circle and base the circumference. This gives a
contradiction, so that triangle cannot have area less than the circle’s.
Supposing that the triangle’s area is greater than the circles leads
to another contradiction on considering a sequence of polygons circumscribed
about the circle-so the two must be exactly equal.
Archimedes does an Integral
Archimedes realized that in finding the area of a circle, another problem
was solved, that of finding the area of the curved surface of a cone (like an
old-fashioned ice-cream cone). If such a cone is opened out by cutting a
straight line up from its point, it will have the shape of a fan-that is, a
segment of a circle. Its area will then be that fraction of the full circle’s
area that its curved edge is of the full circle’s circumference. He also
showed how to find the curved area of a “slice” of a cone, such as
you’d get by cutting off the top of an ice-cream cone, by which we mean
the other end from the point, cutting parallel to the top circle, to get a sort
of ring-shaped bit of cone. He than managed to calculate the surface area of a
sphere. His approach was as follows: imagine where Charlottesville appears on a
globe, on the 38th parallel. This parallel is a ring going all the
way around the globe at a constant distance down from the North Pole. Now consider
the part of the globe surface between this 38th parallel and the 39th
parallel. This is a ribbon of surface going around, and is very close to a
slice of a cone, if we choose a cone of the right size and angle. Archimedes’
strategy was to divide the whole surface into ribbons like this, and find the
area of each ribbon by taking it to be part of a cone. He then summed up the
ribbon areas. Lastly, he took thinner and thinner ribbons to get an accurate
result, using the method of exhaustion to prove that the area of the sphere was
4×pi×r2. This is precisely equivalent to a modern
integral calculus solution of the same problem, and just as rigorous (but more
difficult!)
Conclusion
It is clear from the above discussion that the Greeks laid the essential groundwork
and even began to build the structure of much of modern mathematics. It should
also be emphasized that although some great mathematicians devoted their lives
to this work, it nevertheless took three centuries of cumulative effort, each
building on the previous work. Evidently, this required a stable, literate
culture over many generations. Geometric results are difficult to transmit in
an oral tradition! Recall that Archimedes was killed drawing diagrams in the
sand for his pupils. This level of mathematical analysis attained by
Archimedes, Euclid and others is far in advance of anything recorded by the
Babylonians or Egyptians.
In preparing this lecture I used :
A Source Book in Greek Science, M. R. Cohen and I. E. Drabkin,
Harvard, 1966
previous index next




