BACK

Maxwell's Equations and Electromagnetic Waves

Michael Fowler, Physics Department, UVa

The Equations

Maxwell’s four equations describe the electric and magnetic fields arising from distributions of electric charges and currents, and how those fields change in time.   They were the mathematical distillation of decades of experimental observations of the electric and magnetic effects of charges and currents, plus the profound intuition of Michael Faraday.  Maxwell’s own contribution to these equations is just the last term of the last equation—but the addition of that term had dramatic consequences.  It made evident for the first time that varying electric and magnetic fields could feed off each other—these fields could propagate indefinitely through space, far from the varying charges and currents where they originated.  Previously these fields had been envisioned as tethered to the charges and currents giving rise to them.   Maxwell’s new term (called the displacement current) freed them to move through space in a self-sustaining fashion, and even predicted their velocity—it was the velocity of light!

Here are the equations:

1. Gauss’ Law for electric fields:  

${\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}=q/{\epsilon }_0.$

 (The integral of the outgoing electric field over an area enclosing a volume equals the total charge inside, in appropriate units.)

2. The corresponding formula for magnetic fields:

${\displaystyle \int \overrightarrow{B}\cdot d\overrightarrow{A}}=0.$

(No magnetic charge exists: no “monopoles”.)

3. Faraday’s Law of Magnetic Induction: 

${\displaystyle \oint \overrightarrow{E}\cdot d\overrightarrow{\ell }}=-d/dt\left({\displaystyle \int \overrightarrow{B}\cdot d\overrightarrow{A}}\right).$ 

The first term is integrated round a closed line, usually a wire, and gives the total voltage change around the circuit, which is generated by a varying magnetic field threading through the circuit.

4. Ampere’s Law plus Maxwell’s displacement current: 

${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}={\mu }_0\left(I+\frac{d}{dt}\left({\epsilon }_0{\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}\right)\right).$ 

This gives the total magnetic force around a circuit in terms of the current through the circuit, plus any varying electric field through the circuit (that’s the “displacement current”).

The purpose of this lecture is to review the first three equations and the original Ampere’s law fairly briefly, as they were covered earlier in the course, then to demonstrate why the displacement current term must be added for consistency, and finally to show, without using differential equations, how measured values of static electrical and magnetic attraction are sufficient to determine the speed of light.

 Preliminaries: Definitions of µ₀ and ε₀

Ampere discovered that two parallel wires carrying electric currents in the same direction attract each other magnetically, the force in newtons per unit length being given by

$F=2\left(\frac{{\mu }_0}{4\pi }\right)\frac{I_1{I}_2}{r},$

for long wires a distance $r$ apart. We are using the standard modern units (SI).  The constant ${\mu }_0/4\pi$ that appears here is exactly 10^-7, this defines our present unit of current, the ampere.  To repeat: ${\mu }_0/4\pi$ is not something to measure experimentally, it's just a funny way of writing the number 10^-7!  That's not quite fair—it has dimensions to ensure that both sides of the above equation have the same dimensionality. (Of course, there's a historical reason for this strange convention, as we shall see later).  Anyway, if we bear in mind that dimensions have been taken care of, and just write the equation 

$F=2\cdot {10}^{-7}\cdot \frac{I_1{I}_2}{r},$

it's clear that this defines the unit current—one ampere—as that current in a long straight wire which exerts a magnetic force of $2\times {10}^{-7}$ newtons per meter of wire on a parallel wire one meter away carrying the same current.

However, after we have established our unit of current—the ampere—we have also thereby defined our unit of charge, since current is a flow of charge, and the unit of charge must be the amount carried past a fixed point in unit time by unit current.  Therefore, our unit of charge—the coulomb—is defined by stating that a one amp current in a wire carries one coulomb per second past a fixed point.

 To be consistent, we must do electrostatics using this same unit of charge. Now, the electrostatic force between two charges is $\left(1/4\pi {\epsilon }_0\right)q_1{q}_2/r^2.$ The constant appearing here, now written $1/4\pi {\epsilon }_0$, must be experimentally measured—its value turns out to be $9\times {10}^9$.

 To summarize:  to find the value of $1/4\pi {\epsilon }_0$, two experiments have to be performed. We must first establish the unit of charge from the unit of current by measuring the magnetic force between two current-carrying parallel wires.  Second, we must find the electrostatic force between measured charges. (We could, alternatively, have defined some other unit of current from the start, then we would have had to find both ${\mu }_0$ and ${\epsilon }_0$ by experiments on magnetic and electrostatic attraction.  In fact, the ampere was originally defined as the current that deposited a definite weight of silver per hour in an electrolytic cell). 

Maxwell's Equations

We have so far established that the total flux of electric field out of a closed surface is just the total enclosed charge multiplied by $1/{\epsilon }_0$, $$

${\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}=q/{\epsilon }_0.$

This is Maxwell’s first equation.  It represents completely covering the surface with a large number of tiny patches having areas $d\overrightarrow{A}$.  We represent these small areas as vectors pointing outwards, because we can then take the dot product with the electric field to select the component of that field pointing perpendicularly outwards (it would count negatively if the field were pointing inwards)—this is the only component of the field that contributes to actual flow across the surface.  (Just as a river flowing parallel to its banks has no flow across the banks).

 The second Maxwell equation is the analogous one for the magnetic field, which has no sources or sinks (no magnetic monopoles, the field lines just flow around in closed curves). Thinking of the force lines as representing a kind of fluid flow, the so-called "magnetic flux", we see that for a closed surface, as much magnetic flux flows into the surface as flows out.  This can perhaps be visualized most clearly by taking a group of neighboring lines of force forming a slender tube—the "fluid" inside this tube flows round and round, so as the tube goes into the closed surface then comes out again (maybe more than once) it is easy to see that what flows into the closed surface at one place flows out at another. Therefore the net flux out of the enclosed volume is zero, Maxwell’s second equation:

${\displaystyle \int \overrightarrow{B}\cdot d\overrightarrow{A}}=0.$

The first two Maxwell's equations, given above, are for integrals of the electric and magnetic fields over closed surfaces . The other two Maxwell's equations, discussed below, are for integrals of electric and magnetic fields around closed curves (taking the component of the field pointing along the curve). These represent the work that would be needed to take a charge around a closed curve in an electric field, and a magnetic monopole (if one existed!) around a closed curve in a magnetic field.

 The simplest version of Maxwell's third equation is the electrostatic case:

The path integral ${\displaystyle \oint \overrightarrow{E}\cdot d\overrightarrow{\ell }}=0$ for electrostatics.

However, we know that this is only part of the truth, because from Faraday's Law of Induction, if a closed circuit has a changing magnetic flux through it, a circulating current will arise, which means there is a nonzero voltage around the circuit.

 The full version of Maxwell's third equation is: 

${\displaystyle \oint \overrightarrow{E}\cdot d\overrightarrow{\ell }}=-d/dt\left({\displaystyle \int \overrightarrow{B}\cdot d\overrightarrow{A}}\right)$

where the area integrated over on the right hand side spans the path (or circuit) on the left hand side, like a soap film on a loop of wire.

 It may seem that the integral on the right hand side is not very clearly defined, because if the path or circuit lies in a plane, the natural choice of spanning surface (the "soap film") is flat, but how do you decide what surface to choose to do the integral over for a wire bent into a circuit that doesn’t lie in a plane?   The answer is that it doesn’t matter what surface you choose, as long as the wire forms its boundary.  Consider two different surfaces both having the wire as a boundary (just as both the northern hemisphere of the earth’s surface and the southern hemisphere have the equator as a boundary). If you add these two surfaces together, they form a single closed surface, and we know that for a closed surface ${\displaystyle \int \overrightarrow{B}\cdot d\overrightarrow{A}}=0$.  This implies that ${\displaystyle \int \overrightarrow{B}\cdot d\overrightarrow{A}}$ for one of the two surfaces bounded by the path is equal to $-{\displaystyle \int \overrightarrow{B}\cdot d\overrightarrow{A}}$ for the other one, so that the two will add to zero for the whole closed surface.  But don’t forget these integrals for the whole closed surface are defined with the little area vectors pointing outwards from the enclosed volume. By imagining two surfaces spanning the wire that are actually close to each other, it is clear that the integral over one of them is equal to the integral over the other if we take the $d\overrightarrow{A}$ vectors to point in the same direction for both of them, which in terms of the enclosed volume would be outwards for one surface, inwards for the other one. The bottom line of all this is that the surface integral ${\displaystyle \int \overrightarrow{B}\cdot d\overrightarrow{A}}$ is the same for any surface spanning the path, so it doesn’t matter which we choose. 

The equation analogous to the electrostatic version of the third equation given above, but for the magnetic field, is Ampere's law

${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}={\mu }_0\cdot \text{(enclosed currents)}$

for magnetostatics, where the currents counted are those threading through the path we're integrating around, so if there is a soap film spanning the path, these are the currents that punch through the film (of course, we have to agree on a direction, and subtract currents flowing in the opposite direction).

 We must now consider whether this equation, like the electrostatic one, has limited validity. In fact, it was not questioned for a generation after Ampere wrote it down: Maxwell's great contribution, in the 1860's, was to realize that it was not always valid.

 When Does Ampere's Law Go Wrong?

 A simple example to see that something must be wrong with Ampere's Law in the general case is given by Feynman in his Lectures in Physics.  Suppose we use a hypodermic needle to insert a spherically symmetric blob of charge in the middle of a large vat of solidified jello (which we assume conducts electricity).  Because of electrostatic repulsion, the charge will dissipate, currents will flow outwards in a spherically symmetric way.  Question: does this outward-flowing current distribution generate a magnetic field?  The answer must be no , because since we have a completely spherically symmetric situation, it could only generate a spherically symmetric magnetic field.  But the only possible such fields are one pointing outwards everywhere and one pointing inwards everywhere, both corresponding to non-existent monopoles. So, there can be no magnetic field.

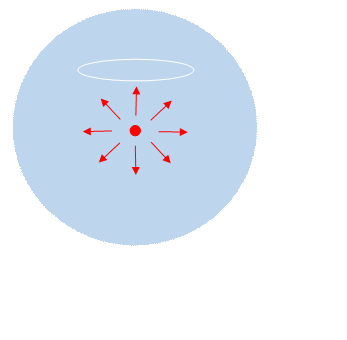 However, imagine we now consider checking Ampere's law by taking as a path a horizontal circle with its center above the point where we injected the charge (think of a halo above someone’s head.)  Obviously, the left hand side of Ampere's equation is zero, since there can be no magnetic field.  (It would have to be spherically symmetric, meaning radial.)  On the other hand, the right hand side is most definitely not zero, since some of the outward flowing current is going to go through our circle.  So the equation must be wrong.

 Ampere's law was established as the result of large numbers of careful experiments on all kinds of current distributions.  So how could it be that something of the kind we describe above was overlooked?  The reason is really similar to why electromagnetic induction was missed for so long. No-one thought about looking at changing fields, all the experiments were done on steady situations.  With our ball of charge spreading outward in the jello, there is obviously a changing electric field.  Imagine yourself in the jello near where the charge was injected: at first, you would feel a strong field from the nearby concentrated charge, but as the charge spreads out spherically, some of it going past you, the field will decrease with time.

Maxwell's Example

Maxwell himself gave a more practical example:  consider Ampere's law for the usual infinitely long wire carrying a steady current $I,$ but now break the wire at some point and put in two large circular metal plates, a capacitor, maintaining the steady current $I$ in the wire everywhere else, so that charge is simply piling up on one of the plates and draining off the other.

 Looking now at the wire some distance away from the plates, the situation appears normal, and if we put the usual circular path around the wire, application of Ampere's law tells us that the magnetic field at distance $r,$ from 

${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}={\mu }_{0}I$

is just

$B={\mu }_{0}I/2\pi r.$

Recall, however, that we defined the current threading the path in terms of current punching through a soap film spanning the path, and said this was independent of whether the soap film was flat, bulging out on one side, or whatever. With a single infinite wire, there was no escape— no contortions of this covering surface could wriggle free of the wire going through it (actually, if you distort the surface enough, the wire could penetrate it several times, but you have to count the net flow across the surface, and the new penetrations would come in pairs with the current crossing the surface in opposite directions, so they would cancel).

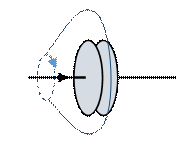 Once we bring in Maxwell's parallel plate capacitor, however, there is a way to distort the surface so that no current penetrates it at all: we can run it between the plates!

The question then arises: can we rescue Ampere's law by adding another term just as the electrostatic version of the third equation was rescued by adding Faraday's induction term? The answer is of course yes: although there is no current crossing the surface if we put it between the capacitor plates, there is certainly a changing electric field , because the capacitor is charging up as the current $I$ flows in. Assuming the plates are close together, we can take all the electric field lines from the charge $q$ on one plate to flow across to the other plate, so the total electric flux across the surface between the plates, 

${\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}=q/{\epsilon }_0.$

Now, the current in the wire $,I,$ is just the rate of change of charge on the plate, 

$I=dq/dt.$

Putting the above two equations together, we see that 

$I=\frac{d}{dt}\left({\epsilon }_0{\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}\right).$

Ampere's law can now be written in a way that is correct no matter where we put the surface spanning the path we integrate the magnetic field around: 

${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}={\mu }_0\left(I+\frac{d}{dt}\left({\epsilon }_0{\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}\right)\right).$

This is Maxwell’s fourth equation.

Notice that in the case of the wire, either the current in the wire, or the increasing electric field, contribute on the right hand side, depending on whether we have the surface simply cutting through the wire, or positioned between the plates. (Actually, more complicated situations are possible—we could imaging the surface partly between the plates, then cutting through the plates to get out!  In this case, we would have to figure out the current actually in the plate to get the right hand side, but the equation would still apply).

"Displacement Current"

Maxwell referred to the second term on the right hand side, the changing electric field term, as the "displacement current".  This was an analogy with a dielectric material.  If a dielectric material is placed in an electric field, the molecules are distorted, their positive charges moving slightly to the right, say, the negative charges slightly to the left.  Now consider what happens to a dielectric in an increasing electric field.  The positive charges will be displaced to the right by a continuously increasing distance, so, as long as the electric field is increasing in strength, these charges are moving: there is actually a displacement current .  (Meanwhile, the negative charges are moving the other way, but that is a current in the same direction, so adds to the effect of the positive charges' motion.)  Maxwell's picture of the vacuum, the aether, was that it too had dielectric properties somehow, so he pictured a similar motion of charge in the vacuum to that we have just described in the dielectric.  The picture is wrong, but this is why the changing electric field term is often called the "displacement current", and in Ampere's law (generalized) is just added to the real current, to give Maxwell's fourth—and final—equation. 

Another Angle on the Fourth Equation: the Link to Charge Conservation

Going back for a moment to Ampere's law, we stated it as:

  

${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}={\mu }_0\cdot \text{(enclosed currents)}$

for magnetostatics, where the currents counted are those threading through the path we’re integrating around, so if there is a soap film spanning the path, these are the currents that punch through the film. Our mental picture here is usually of a few thin wires, maybe twisted in various ways, carrying currents. More generally, thinking of electrolytes, or even of fat wires, we should be envisioning a current density varying from point to point in space. In other words, we have a flux of current and the natural expression for the current threading our path is (analogous to the magnetic flux in the third equation) to write a surface integral of the current density $\overrightarrow{j}$ over a surface spanning the path, giving for magnetostatics 

path integral ${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}={\mu }_0{\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}$(surface integral, over surface spanning path)

The question then arises as to whether the surface integral we have written on the right hand side above depends on which surface we choose spanning the path. From an argument exactly parallel to that for the magnetic flux in the third equation (see above), this will be true if and only If ${\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}=0$  for a closed surface (with the path lying in the surface—this closed surface is made up by combining two different surfaces spanning the path).

 Now, ${\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}$  taken over a closed surface is just the net current flow out of the enclosed volume. Obviously, in a situation with steady currents flowing along wires or through conductors, with no charge piling up or draining away from anywhere, this is zero. However, if the total electric charge $q,$ say, enclosed by the closed surface is changing as time goes on, then evidently 

${\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}=-dq/dt,$

where we put in a minus sign because, with our convention, $d\overrightarrow{A}$ is a little vector pointing outwards, so the integral represents net flow of charge out from the surface, equal to the rate of decrease of the enclosed total charge.

 To summarize: if the local charge densities are changing in time, that is, if charge is piling up in or leaving some region, then ${\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}\ne 0$ over a closed surface around that region. That implies that ${\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}$ over one surface spanning the wire will be different from ${\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}$ over another surface spanning the wire if these two surfaces together make up a closed surface enclosing a region containing a changing amount of charge.

 The key to fixing this up is to realize that although ${\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}=-dq/dt\ne 0,$ the right-hand side can be written as another surface integral over the same surface, using the first Maxwell equation, that is, the integral over a closed surface

${\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}=q/{\epsilon }_0$

where $q$ is the total charge in the volume enclosed by the surface. 

By taking the time rate of change of both sides, we find 

$\frac{d}{dt}{\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}=\frac{1}{{\epsilon }_0}\frac{dq}{dt}$

Putting this together with ${\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}=-dq/dt$ gives: 

${\epsilon }_0\frac{d}{dt}{\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}+{\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}=0$

for any closed surface, and consequently this is a surface integral that must be the same for any surface spanning the path or circuit!  (Because two different surfaces spanning the same circuit add up to a closed surface. We’ll ignore the technically trickier case where the two surfaces intersect each other, creating multiple volumes—there one must treat each created volume separately to get the signs right.) 

Therefore, this is the way to generalize Ampere's law from the magnetostatic situation to the case where charge densities are varying with time, that is to say the path integral

${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}={\mu }_0{\displaystyle \int \left(\overrightarrow{j}+{\epsilon }_0\frac{d\overrightarrow{E}}{dt}\right)}\cdot d\overrightarrow{A}$

and this gives the same result for any surface spanning the path. 

A Sheet of Current: A Simple Magnetic Field

As a preliminary to looking at electromagnetic waves, we consider the magnetic field configuration from a sheet of uniform current of large extent.  Think of the sheet as perpendicular to this sheet of paper, the current running vertically upwards.  It might be helpful to visualize the sheet as many equal parallel fine wires uniformly spaced close together: 

...................................................................................... (wires)

The magnetic field from this current sheet can be found using Ampere's law applied to a rectangular contour in the plane of the paper, with the current sheet itself bisecting the rectangle, so the rectangle's top and bottom are equidistant from the current sheet in opposite directions.

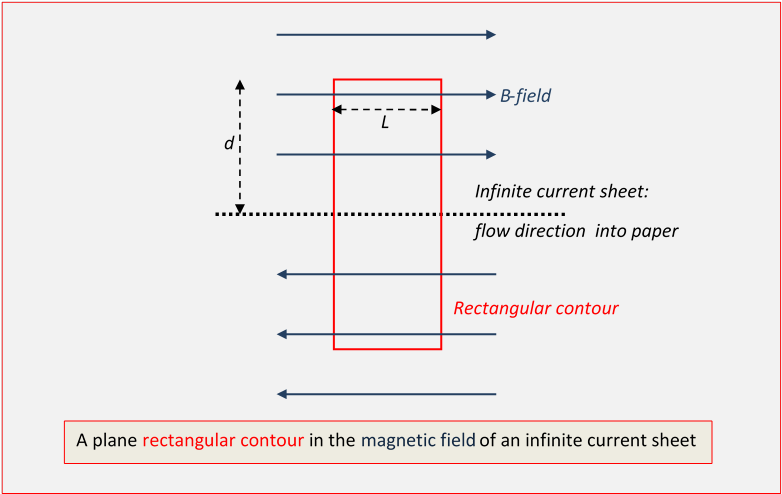
 Applying Ampere’s law to the above rectangular contour, there are contributions to ${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}$ only from the top and bottom, and they add to give $2BL$ if the rectangle has side $L.$ The total current enclosed by the rectangle is $IL,$ taking the current density of the sheet to be $I$ amperes per meter (how many little wires per meter multiplied by the current in each wire). 

Thus, ${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}={\mu }_0\cdot \text{(enclosed currents)}$ immediately gives: 

$B={\mu }_{0}I/2$

a magnetic field strength independent of distance $d$ from the sheet. (This is the magnetostatic analog of the electrostatic result that the electric field from an infinite sheet of charge is independent of distance from the sheet.)  In real life, where there are no infinite sheets of anything, these results are good approximations for distances from the sheet small compared with the extent of the sheet. 

Switching on the Sheet: How Fast Does the Field Build Up?

Consider now how the magnetic field develops if the current in the sheet is suddenly switched on at time $t=0.$ We will assume that sufficiently close to the sheet, the magnetic field pattern found above using Ampere's law is rather rapidly established.  

In fact, we will assume further that the magnetic field spreads out from the sheet like a tidal wave, moving in both directions at some speed $v,$ so that after time $t$ the field within distance $vt$ of the sheet is the same as that found above for the magnetostatic case, but beyond $vt$ there is at that instant no magnetic field present.

Let us now apply Maxwell's equations to this guess to see if it can make sense. Certainly Ampere's law doesn't work by itself, because if we take a rectangular path as we did in the previous section, for $d<vt$ everything works as before, but for a rectangle extending beyond the spreading magnetic field, $d>vt,$ there will be no magnetic field contribution from the top and bottom of the rectangle, and hence 

${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}=0$

but there is definitely enclosed current!  

We are forced to conclude that for Maxwell's fourth equation to be correct, there must also be a changing electric field through the rectangular contour. 

Let us now try to nail down what this electric field through the contour must look like.  First, it must be through the contour, that is, have a component perpendicular to the plane of the contour, in other words, perpendicular to the magnetic field.  In fact, electric field components in other directions won't affect the fourth equation we are trying to satisfy, so we shall ignore them.  Notice first that for a rectangular contour with $d<vt,$  Ampere's law works, so we don't want a changing electric field through such a contour (but a constant electric field would be ok). 

Now apply Maxwell's fourth equation to a rectangular contour with $d>vt,$  

It is:  path integral ${\displaystyle \oint \overrightarrow{B}\cdot d\overrightarrow{\ell }}={\mu }_0{\displaystyle \int \left(\overrightarrow{j}+{\epsilon }_0\frac{d\overrightarrow{E}}{dt}\right)}\cdot d\overrightarrow{A}$ (over surface spanning path).   

For the rectangle shown above, the integral on the left hand side is zero because $\overrightarrow{B}$ is perpendicular to $d\overrightarrow{\ell }$ along the sides, so the dot product is zero, and $\overrightarrow{B}$ is zero at the top and bottom, because the outward moving "wave" of magnetic field hasn’t gotten there yet. Therefore, the right hand side of the equation must also be zero. 

We know ${\displaystyle \int \overrightarrow{j}}\cdot d\overrightarrow{A}=LI$, so we must have:  ${\epsilon }_0\frac{d}{dt}{\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}=-LI.$ 

Finding the Speed of the Outgoing Field Front: the Connection with Light

So, as long as the outward moving front of magnetic field, travelling at $v,$ hasn't reached the top and bottom of the rectangular contour, the electric field through the contour increases linearly with time, but the increase drops to zero (because Ampere's law is satisfied) the moment the front reaches the top and bottom of the rectangle. The simplest way to get this behavior is to have an electric field of strength $E,$ perpendicular to the magnetic field, everywhere there is a magnetic field, so the electric field also spreads outwards at speed $v.$  Note that, unlike the magnetic field, the electric field must point the same way on both sides of the current sheet, otherwise its net flux through the rectangle would be zero. 

After time $t,$ then, the electric field flux through the rectangular contour ${\displaystyle \int \overrightarrow{E}}\cdot d\overrightarrow{A}$ will be just field x area = $E\cdot 2\cdot vtL,$ and the rate of change will be $2EvL.$ (It's spreading both ways, hence the 2). 

Therefore

${\epsilon }_{0}E\cdot 2\cdot vtL=-LI,$

the electric field is downwards and of strength $E=I/\left(2{\epsilon }_{0}v\right).$ 

Since $B={\mu }_{0}I/2,$ this implies: 

$B={\mu }_0{\epsilon }_{0}vE.$ 

But we have another equation linking the field strengths of the electric and magnetic fields, Maxwell's third equation: 

${\displaystyle \oint \overrightarrow{E}\cdot d\overrightarrow{\ell }}=-d/dt\left({\displaystyle \int \overrightarrow{B}\cdot d\overrightarrow{A}}\right)$

We can apply this equation to a rectangular contour with sides parallel to the $E$ field, one side being within $vt$ of the current sheet, the other more distant, so the only contribution to the integral is $EL$  from the first side, which we take to have length $L.$ (This contour is all on one side of the current sheet.) The area of the rectangle the magnetic flux is passing through will be increasing at a rate $Lv$ (square meters per second) as the magnetic field spreads outwards. 

It follows that 

$E=vB.$ 

Putting this together with the result of the fourth equation, 

$B={\mu }_0{\epsilon }_{0}vE,$ 

we deduce

$$v^2=\frac{1}{{\mu }_0{\epsilon }_0}.$$ 

Substituting the defined value of ${\mu }_0,$ and the experimentally measured value of ${\epsilon }_0,$  we find that the electric and magnetic fields spread outwards from the switched-on current sheet at a speed of 3 x 10⁸ meters per second. 

This is how Maxwell discovered a speed equal to the speed of light from a purely theoretical argument based on experimental determinations of forces between currents in wires and forces between electrostatic charges. This of course led to the realization that light is an electromagnetic wave, and that there must be other such waves with different wavelengths.  Hertz detected other waves, of much longer wavelengths, experimentally, and this led directly to radio, tv, radar, etc.