According to Heath, this proof is really due to Archimedes. It should be mentioned that it is of course a lot easier to prove the result using trigonometry! The area of a triangle is 1/2ab.sinC, and using c²=a²+b²-2ab.cosC, and sin²+cos²=1, the result follows in a few lines.

 

Here they are:

                                                

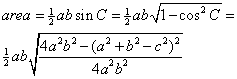
Note that the ab outside cancels that inside, so all we have to do is rearrange the numerator inside. For convenience, I change the overall sign of the expression to get:

 

(a² + b² – c²)² - 4a²b²  =  (a²-b²)² – 2c²(a² +b²) + c⁴

 

                                    = ((a + b)² – c²)((a – b)² – c²)

                                   

                                    = (a + b + c)(a + b – c)(a – b + c)(a – b – c)

 

QED