APPENDIX E

VECTORS

Introduction

            Many physical quantities can be completely described by just one number.  Such quantities are called scalar quantities.  Examples of scalar quantities are mass, length, area, energy, temperature, etc.  For other quantities, called vectors, a single number is not enough.  A force F requires three numbers to be completely described.[1]  These three numbers depend on the coordinate system in which the vector is chosen to be described.  In any particular coordinate system, then, these three numbers are simply the projections of the vector on the three coordinates of the system.  The vector itself is usually represented as a list of the numbers enclosed by parentheses.  For example,

 

                                                                 .                                                     (1)

 

Here, the subscripts correspond to the coordinates of the system.

 

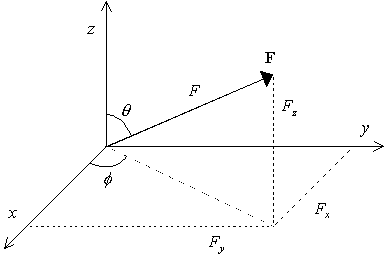
            In Cartesian coordinates, the three numbers are the lengths, Fx, Fy, and Fz, of the vector F’s projections onto the x-, y-, and z-axes.  Fx, Fy, and Fz are called the x-, y-, or z- ‘compo­nents’ of  F.  The length of a vec­tor, , expressed in terms of its components, is easi­ly found by using Pythagoras’ theorem:

 

Fig. 1

   .  (2)

 

In spherical coordinates, the three numbers are the length F of the vector, the angle θ that it makes with the z‑axis and the angle  that its projec­tion onto the x-y plane makes with the x‑axis (see Fig. 1).

 

            One can translate from one coordinate system to another.  To translate from spherical into Cartesian coordinates, we must represent the Cartesian components in terms of spherical coordinates:

 

                                              (3)

 

Other examples of physical vectors, other than force, include velocity, momentum, accelera­tion, as well as their corresponding angular siblings, angular velocity, angular momentum, angular accelera­tion, and torque.

 

Vector Algebra

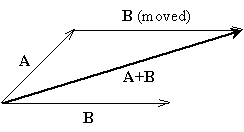
Fig. 2.  Addition of two vectors A and B in the plane, i.e. in two dimen­sions.

            The mathematical field of vector algebra has been developed to allow for computation of vector quantities.  Vectors can be added graphically in the manner shown in Fig. 2.

  The vector B is shifted without changing its direction until its ‘tail’ abuts the tip of vector A.  The ‘sum vector’ or the ‘vector sum’ A + B is the vector extending from the tail of the vector A to the tip of the shifted vector B.

 

            Algebraically two vectors are added by adding their components.  Therefore if Ax, Ay, and Az are the com­po­nents of a vector A and Bx, By, and Bz are the com­ponents of a vector B, then the sum vector will be given by adding their components:

 

                         , , and              (4)

 

Put a different way,

 

                                        (5)

 

Similarly the difference of two vectors, A - B, is taken graphi­cal­ly by inverting the direction of B and then proceeding as in Fig. 2.  Algebraically the difference of two vectors is taken by taking the difference of the components, i.e.

 

                                         (6)

 

            As is often the case in mathematics, using a notation that fits the problem will help things along.  Vectors are often written in a different form:

                                                                             

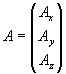                                                                                                                                (7)

 

In this notation, the sum of two vectors A and B simply becomes

 

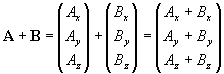                                                                                         (8)

 

Given two vectors A and B that form an angle θAB the product is defined as

 

                                                                                                                  (9)

 

This product is called the dot product or scalar product.  It is particularly easy to calculate using the notation of Eq. 7,

 

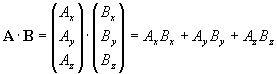                                           ,                             (10)

 

i.e. one simply writes the two vectors side by side, multiplies the numbers in each line and adds up all the products.  The result is a single number, a scalar, hence the name.  The scalar product is distinguished from the cross product, which we shall not discuss here in detail.  We just mention in passing that the cross product of two vectors is another vector whose length is given by

 

                                                                                                               (11)

 

and whose orientation is orthogonal to both the vector A and the vector B. An example of the cross product is the torque vector

 

                                                                                                                               (12)

 

 


[1]To distinguish it from a scalar, a vector is, in print, usually represented by a boldface letters, in our example F. The length or magnitude of the same vector is, then, represented by the same letter in lightface, F.