Physics 152: Homework Problems on
Fluids
6/1/07
1. Atmospheric pressure varies
from day to day, but 1 atm is defined as 1.01 x 105
2. The density of air at room
temperature is about 1.29 kg/m3. Use this together with the
definition of 1 atm as 1.01 x 105 
. Use your result to
estimate the atmospheric pressure on top of the Blue Ridge (say 4000 feet),
Snowmass (11,000 feet) and
3. As a practical matter, how would you measure the density of air in a room? Actually, Galileo did this in the early 1600’s. Can you figure out how he managed to do it? (His result was off by a factor of two, but that was still pretty good!)
4. A ball is floating in water, exactly half submerged, as shown in the diagram. Oil is now poured gently onto the water, so that it does not mix, but forms a layer above the water. The oil completely covers the ball. Is the center of the ball now above, below or at the water-oil boundary?
5. A weather balloon is made of latex, filled with helium (but not stretched) so that it can just lift an instrument package of 10 kg., including the weight of the balloon.
(a) What, approximately, is the volume of the balloon?
(b) The balloon lifts the package slowly to a height of 6 km., where atmospheric pressure is one-half of that at ground level. Assume (falsely!) that the air temperature is the same. How big is the balloon at 6 km.?
(c) How does the lifting capacity of the balloon at 6 km compare with that at ground level?
(Note: actually these balloons can get to 30 km.)
6. I
make salad dressing in a conical bottle, wide at the base, steadily narrowing
up to the neck. I pour in 100 cc of vinegar, then add 100 cc of olive oil. The
oil is a layer on top of the vinegar. Then I shake it vigorously, so the two
liquids are completely mixed together.
How (if at all) does the
pressure on the bottom after shaking differ from the pressure on the bottom
before shaking?
7.
If an ice cube is floating in a glass filled to the brim with water,
what happens to the water level as the ice cube melts? Would your answer be the
same if the ice cube were stuck to the glass and fully submerged?
8. (a) State the Law of Atmospheres: the equation relating the density of air to height above the Earth’s surface. (You don’t have to derive it, just state it.)
(b) Given that the density of the atmosphere at 3,500 meters is approximately 2/3 that at sea level, sketch a rough graph of density with height up to 14,000 meters. (Take sea level density 1.3 kg/m3.)
(c) In 1804, a French chemist, Gay-Lussac, went up in a balloon to about 7,000 meters to check the chemistry of the atmosphere. The balloon was filled with hydrogen. Make a very rough estimate of the size of the balloon. (Guess Gay-Lussac’s weight, assume the balloon weighed three times as much as he did.)
9. A modern hot air balloon can weigh about 4 tons, fully loaded. The maximum operating temperature for the enclosed hot air is 120 degrees C. (Otherwise the nylon interior deteriorates rapidly.) Assume the enclosed hot air is at 100 degrees, and the outside atmosphere is at zero degrees. If the balloon can just lift off, how big is it?
10. You have a
solid metal cylinder, of height h, cross section area A, and
density 
, standing on its end on a table. What is the pressure on the
table underneath the cylinder? Suppose
you now heat the cylinder, and it expands by the same percentage in all
directions (so the shape and proportions are unchanged), the height increasing
to 
. What is the pressure
on the table now?
11. Assume you are walking around underwater, breathing through a flexible plastic tube, the other end held on the surface by some floating object. The object is to estimate how far underwater it’s safe for you to go.
(a) Assume first you are out of the water, lying flat on your back, with a weight evenly distributed across your chest. What weight would cause you difficulty in breathing?
(b) Now, make a guess as to the area of your chest over the lungs, and deduce at what depth the water pressure on your chest would become dangerous.
12. Figure out what total area of one tire of your automobile is in contact with the road when the vehicle is parked on level ground.
13. What is the approximate pressure your shoes exert on the ground when you’re standing still? Give a ballpark estimate for the pressure exerted by a woman balancing on one high heel.
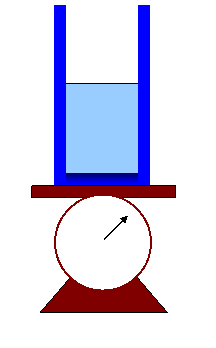
14. A beaker containing water is placed on a spring scale as shown. Next, a cork of mass 10 grams, and density 200 kg/m3, is gently floated on the water, not touching the sides of the container.
(a) How does that change the scale reading?
(b) A thin rod, of negligible volume, is now used to push the cork underwater, again without it touching the container? Does that change the scale reading? Explain your reasoning.
(c) What if the cork is held underwater by a thin string attached to a small hook in the middle of the base of the container? What does the scale read in that case? Does the tension in the string play a role?
15. In a car going down a highway at a steady velocity, a child has a helium-filled balloon on a string, the balloon is at rest directly above the child, not touching the roof of the car. Now the driver accelerates. How does the balloon move? Explain your reasoning.
16. (a) Explain how a nonvertical jet can keep a beach ball in the air.
(b) Write down your best guesses for the weight and size of the (very light!) beach ball, etc., then use them to make a ballpark estimate of the speed of the air in the jet holding the ball up.
17. In the flow meter shown, air flows from a pipe of cross sectional area 10 sq cm into one of cross sectional area 40 sq cm. The manometer contains water, the height difference between the two arms is 5 cm. What is the rate of air flow?
18. A large beer keg of height H and cross-section area A1 is filled with beer. The top is open to atmospheric pressure. At the bottom is a spigot opening of area A2, which is much smaller than A1.
(a) Show that when the height of the beer is h, the speed of the beer leaving the spigot is approximately Ö(2gh).
(b) Show that for the approximation A2 <<A1, the rate of change of the height h of the beer is given by
(c) Find h as a function of time if h = H at t = 0.
(d) Find the total time needed to drain the keg if H = 2 m, A1 = 0.8 m2, and A2 = (10-4)A1.
19. (a) Write down the equation that defines the coefficient of viscosity h.
(b) By balancing dimensions on both sides of your equation, find the dimensions M?L?T? of h.
(c) What are the dimensions of flow rate of blood through an artery?
(d) What are the dimensions of the pressure gradient (pressure drop per unit length) in an artery?
(e) Assuming that the blood flow rate depends only on the pressure gradient, the viscosity and the radius R of the artery, give a proof using dimensions, and showing all your steps, that the flow rate is proportional to R4.
(f) If plaque build up in an artery reduces its radius by 10%, estimate how much the blood flow is reduced if the blood pressure stays the same.
20. A simple hot tub has vertical sides, water depth one meter and area 4 square meters. It has a drain at the bottom, a circular opening of radius 3 cm. When the plug is pulled, it drains gravitationally (no pump).
(a) What is the speed of water flow through the circular opening right after the plug is pulled? (Ignore viscosity: assume the water is flowing at this same speed over the whole area of the opening.)
(b) At what speed is the water level in the tub dropping right after the plug is pulled?
(c) How quickly is the level in the tub dropping when the tub is half empty?
(d) How long does it take for the tub to empty
completely?
21. Suppose a mass m of fluid moving at v1 in the x-direction mixes with a mass m moving at v2 in the x-direction. Momentum conservation tells us that the mixed mass 2m moves at ½( v1 + v2). Prove that the total kinetic energy has decreased if v1, v2 are unequal.
22. Using only dimensional arguments, derive the depth dependence of the steady flow of a wide river under gravity. (Note: The appropriate flow rate is cubic meters per second per meter of width of the river.)
23. Plot on a graph the velocity profiles for two
rivers, one of depth h and one 2h, having the same values of 
What is the ratio of the surface
velocities of the two rivers? Suppose that one meter below the surface of one
of the rivers, the water is flowing 0.5 m.sec-1 slower than it is
flowing at the surface. Would that also be true of the other river?
24. Assuming the flow pattern in the diagram has
the same proportions for different radii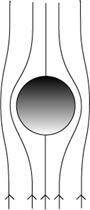 
(so for a larger radius ball it’s the same
pattern magnified), how does the fluid velocity gradient near the
“equator” of the ball change on going from a ball of radius a to one of
radius 2a? (Assume the two balls are falling through the fluid at
the same speed.) Argue that most of the viscous drag on the sphere takes
place in a band surrounding the equator (so, a band shaped like the tropical
zone on the earth). From this, make plausible that the total viscous drag
will be proportional to the sphere’s radius, not to the square of the radius.
25. An aged professor vigorously cleaning a
blackboard raises a cloud of chalk dust that takes several minutes to
settle. From this information, make some
estimate of the size of chalk particles in the cloud. Also state whether the drag force from the
air on the particles is mainly viscous or mainly inertial (for air 
).
26. Imagine a foggy day when the air is still. Actually, the fog is made up of tiny spherical droplets of water. The fog obviously doesn’t fall to the ground very fast. Use this fact to make some estimate of the probable maximum size of the droplets.
27. (a) A room freshener sprays out a mist of tiny water droplets (containing some odor neutralizer which has a negligible effect on the density of the droplets). It is claimed that the mist will stay in the air for 30 minutes. Assuming the air in the room is still, and neglecting possible evaporation from the droplets, figure out from this the approximate size of the droplets.
(b) Justify any formula you use by finding a Reynolds number.
28. After a storm, some rivers and lakes become muddy. Assume the mud particles have the density of ordinary rock, say 2500 kg per cubic meter, and assume they are spherical to a good approximation. If the still water in a lake one meter deep takes two days for the mud to settle to the bottom, use Stokes’ Law to give a ballpark estimate of the size of the mud particles.
29. By staring at a fizzy drink,
make some estimate of the size and speed of a typical bubble rising to the top.
Pick the smallest one you can comfortably see and try to time its speed—or make
an estimate. What, very approximately,
is the Reynolds number for the flow of liquid around the bubble? Is the bubble
impeded in its rise mainly by viscous or by inertial forces? (Use the
value of 
for water at room temperature,
=1mPa.sec.)
30. Estimate what would be the maximum height of a wall you could jump off and be pretty certain of landing without breaking anything (I’m not responsible if you try this!), and, from that estimate, figure out a reasonable size for the diameter of a parachute.
31. Take the following simple model of a skydiver: suppose that as he falls, all the air is his direct path is deflected sideways just as if it bounced off him, imagining his downward profile to be V-shaped. Ignore viscosity. By making reasonable estimates of the size and weight of the skydiver, figure out his terminal velocity.
32. (a) Write down the definition of the Reynold’s number.
(b) Give a ballpark estimate for the Reynold’s number for airflow around a car moving down the highway at 20 m×sec-1 on a day when there is no wind.
(c) From your estimate above, how significant is the viscosity of the air in the drag force?
(d) If we assume the drag force F only depends on the density of the air r, the dimensions of the car a, and the speed of the car v, show from dimensional arguments that F = Cra2v2, where C is a constant.
(e) Take C = 0.2 and give an estimate of this force for your car. You can take a value for r accurate to one significant figure. State clearly what you take for a2.
(f) What power in kilowatts is the car expending in overcoming this drag force at 20 m×sec-1?
(g) How much would this power go up if the speed were doubled?
33. (a) Prove by a dimensional argument that the
drag force on a falling sphere caused by pushing air aside has the form 
, where C is a
constant, ρ is the air density, a is the radius of the sphere, and v
its speed.
(b) You are jogging a 7½ minute mile in light rain. There is no wind, the rain appears to you to be coming down towards you at a 45° angle. How fast is the rain falling, in mph and in m sec-1? (1 mile = 1.6 km.)
(c) For raindrops, the C in the formula in part (a) is approximately 1. Use this to find the size of the raindrops in part (b). (Take air density = 1.3 kg/m3, g = 10 m.sec-2.)
(d) Find the Reynolds number. Was it OK to neglect viscous drag?
(e) Would you expect a different answer for raindrop size if you were jogging under identical conditions, and seeing the same angle of fall, but at a high altitude resort? Why?