Visualizing Gravity: the Gravitational Field

Michael Fowler

Introduction

Let’s begin with the definition of gravitational field:

The gravitational field at any point P in space is defined as the gravitational force felt by a tiny unit mass placed at P.

So, to visualize the gravitational field, in this room or on a bigger scale such as the whole Solar System, imagine drawing a vector representing the gravitational force on a one kilogram mass at many different points in space, and seeing how the pattern of these vectors varies from one place to another (in the room, of course, they won’t vary much!). We say “a tiny unit mass” because we don’t want the gravitational field from the test mass itself to disturb the system. This is clearly not a problem for a one kilogram mass in discussing planetary and solar gravity.

To build an intuition of what various gravitational fields look like, we’ll examine a sequence of progressively more interesting systems, beginning with a simple point mass and working up to a hollow spherical shell, this last being what we need to understand the Earth’s own gravitational field, both outside and inside the Earth.

Field from a Single Point Mass

This is of course simple: we know this field has strength $G M / r^{2},$ and points towards the mass $—$ the direction of the attraction. Let’s draw it anyway, or, at least, let’s draw in a few vectors showing its strength at various points:

This is a rather inadequate representation: there’s a lot of blank space, and, besides, the field attracts in three dimensions, there should be vectors pointing at the mass in the air above (and below) the diagram. But the picture does convey the general idea.

A different way to represent a field is to draw “field lines”, curves such that at every point along the curve’s length, its direction is the direction of the field at that point. Of course, for our single mass, the field lines add little insight:

The arrowheads indicate the direction of the force, which points the same way all along the field line. A shortcoming of the field lines picture is that although it can give a good general idea of the field, there is no precise indication of the field’s strength at any point. However, as is evident in the diagram above, there is a clue: where the lines are closer together, the force is stronger. Obviously, we could put in a spoke-like field line anywhere, but if we want to give an indication of field strength, we’d have to have additional lines equally spaced around the mass, and in three dimensions.

Gravitational Field for Two Masses

The next simplest case is two equal masses. Let us place them symmetrically above and below the $x$ -axis:

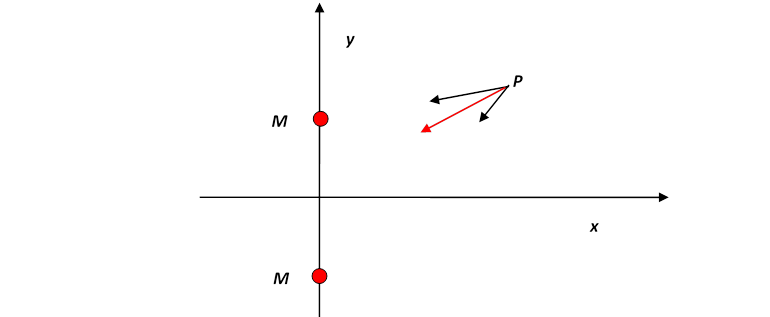
Recall Newton’s Universal Law of Gravitation states that any two masses have a mutual gravitational attraction $G m_{1} m_{2} / r^{2} .$ A point mass $m = 1$ at $P$ will therefore feel gravitational attraction towards both masses $M,$ and a total gravitational field equal to the vector sum of these two forces, illustrated by the red arrow in the figure.

The Principle of Superposition

The fact that the total gravitational field is just given by adding the two vectors together is called the Principle of Superposition. This may sound really obvious, but in fact it isn’t true for every force found in physics: the strong forces between elementary particles don’t obey this principle, neither do the strong gravitational fields near black holes. But just adding the forces as vectors works fine for gravity almost everywhere away from black holes, and, as you will find later, for electric and magnetic fields too. Finally, superposition works for any number of masses, not just two: the total gravitational field is the vector sum of the gravitational fields from all the individual masses. Newton used this to prove that the gravitational field outside a solid sphere was the same as if all the mass were at the center by imagining the solid sphere to be composed of many small masses $—$ in effect, doing an integral, as we shall discuss in detail later. He also invoked superposition in calculating the orbit of the Moon precisely, taking into account gravity from both the Earth and the Sun.

Exercise: For the two mass case above, sketch the gravitational field vector at some other points: look first on the $x$ -axis, then away from it. What do the field lines look like for this two mass case? Sketch them in the neighborhood of the origin.

Field Strength at a Point Equidistant from the Two Masses

It is not difficult to find an exact expression for the gravitational field strength from the two equal masses at an equidistant point $P .$

Choose the $x, y$ axes so that the masses lie on the $y$ -axis at $(0, a)$ and $(0, - a) .$

By symmetry, the field at $P$ must point along the $x$ -axis, so all we have to do is compute the strength of the $x$ -component of the gravitational force from one mass, and double it.

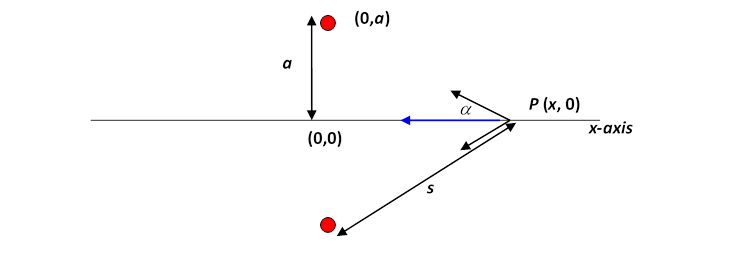
If the distance from the point $P$ to one of the masses is $s,$ the gravitational force towards that mass has strength $G M / s^{2} .$ This force has a component along the $x$ -axis equal to $(G M / s^{2}) \cos α,$ , where $α$ is the angle between the line from $P$ to the mass and the $x$ -axis, so the total gravitational force on a small unit mass at $P$ is $2 (G M / s^{2}) \cos α$ directed along the $x$ -axis.

From the diagram, $\cos α = x / s,$ so the force on a unit mass at $P$ from the two masses $M$ is

$F = - \frac{2 G M x}{{(x^{2} + a^{2})}^{3 / 2}}$

in the $x$ -direction. Note that the force is exactly zero at the origin, and everywhere else it points towards the origin.

Gravitational Field from a Ring of Mass

Now, as long as we look only on the $x$ -axis, this identical formula works for a ring of mass $2 M$ in the $y, z$ plane! It’s just a three-dimensional version of the argument above, and can be visualized by rotating the two-mass diagram above around the $x$ -axis, to give a ring perpendicular to the paper, or by imagining the ring as made up of many beads, and taking the beads in pairs opposite each other.

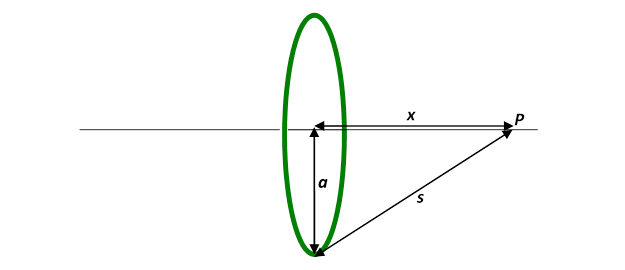
Bottom line: the field from a ring of total mass $M,$ radius $a,$ at a point $P$ on the axis of the ring distance $x$ from the center of the ring is

$F = - \frac{G M x}{{(x^{2} + a^{2})}^{3 / 2}} .$

*Field Outside a Massive Spherical Shell

This is an optional section: you can safely skip to the result on the last line. In fact, you will learn an easy way to derive this result using Gauss’s Theorem when you do Electricity and Magnetism. I just put this section in so you can see that this result can be derived by the straightforward, but quite challenging, method of adding the individual gravitational attractions from all the bits making up the spherical shell.

What about the gravitational field from a hollow spherical shell of matter? Such a shell can be envisioned as a stack of rings.

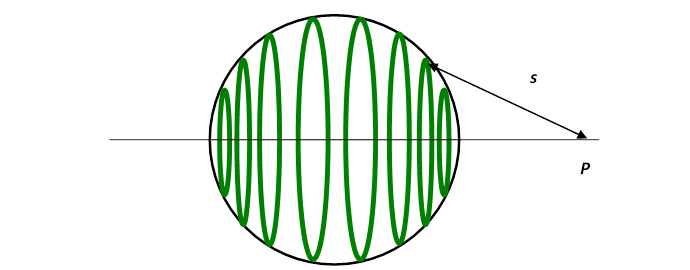
To find the gravitational field at the point $P,$ we just add the contributions from all the rings in the stack.

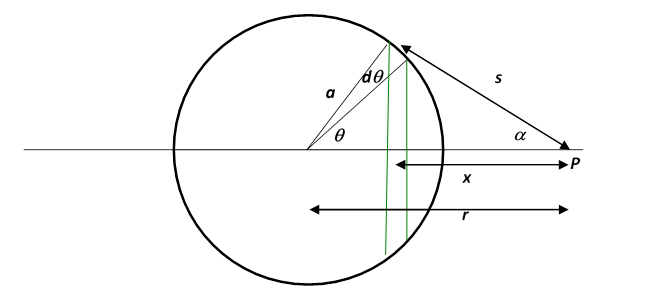
In other words, we divide the spherical shell into narrow “zones”: imagine chopping an orange into circular slices by parallel cuts, perpendicular to the axis $—$ but of course our shell is just the skin of the orange! One such slice gives a ring of skin, corresponding to the surface area between two latitudes, the two parallel lines in the diagram above. Notice from the diagram that this “ring of skin” will have radius $a \sin θ .$ , therefore circumference $2 π a \sin θ$ and breadth $a d θ,$ where we’re taking $d θ$ to be very small. This means that the area of the ring of skin is

$length \times breadth = 2 π a \sin θ \times a d θ .$

So, if the shell has mass $ρ$ per unit area, this ring has mass $2 π a^{2} ρ \sin θ d θ,$ and the gravitational force at $P$ from this ring will be

$F (ring d θ) = - \frac{2 G x π a^{2} ρ \sin θ d θ}{{(x^{2} + a^{2})}^{3 / 2}} .$

Now, to find the total gravitational force at $P$ from the entire shell we have to add the contributions from each of these “rings” which, taken together, make up the shell. In other words, we have to integrate the above expression in $θ from θ = 0 to θ = π .$

So the gravitational field is:

$F = - \int_{0}^{π} \frac{2 G x π a^{2} ρ \sin θ d θ}{{(x^{2} + a^{2})}^{3 / 2}} = - \int_{0}^{π} \frac{2 G x π a^{2} ρ \sin θ d θ}{s^{3}} .$

Notice both $x$ and $s$ are varying! The integral turns out to be easiest done by switching variables from $θ$ to $s .$

Label the distance from $P$ to the center of the sphere by $r .$ Then, from the diagram above, $s^{2} = r^{2} + a^{2} - 2 a r \cos θ,$ and $a, r$ are constants, so $s d s = a r \sin θ d θ,$ and

$F = - \int_{0}^{π} \frac{2 G x π a^{2} ρ \sin θ d θ}{s^{3}} = - \int_{r - a}^{r + a} \frac{2 G x π a^{2} ρ}{s^{3}} \cdot \frac{s d s}{a r} = - \frac{2 G a^{2} ρ π}{a r} \int_{r - a}^{r + a} \frac{x d s}{s^{2}} .$

and from the diagram $a^{2} = s^{2} + r^{2} - 2 s r \cos α,$ so $x = \frac{s^{2} + r^{2} - a^{2}}{2 r},$

and, writing $4 π a^{2} ρ = M,$

$F = \frac{G M}{4 a r^{2}} \int_{r - a}^{r + a} (1 + \frac{r^{2} - a^{2}}{s^{2}}) d s = \frac{G M}{4 a r^{2}} (2 a + (r^{2} - a^{2}) (\frac{1}{r - a} - \frac{1}{r + a})) = \frac{G M}{r^{2}} .$

The derivation was rather lengthy, but the answer is simple:

The gravitational field outside a uniform spherical shell is $G M / r^{2}$ towards the center.

And, there’s a bonus: for the ring, we only found the field along the axis, but for the spherical shell, once we’ve found it in one direction, the whole problem is solved $—$ for the spherical shell, the field must be the same in all directions.

Field Outside a Solid Sphere

Once we know the gravitational field outside a shell of matter is the same as if all the mass were at a point at the center, it’s easy to find the field outside a solid sphere: that’s just a nesting set of shells, like spherical Russian dolls. Adding them up,

The gravitational field outside a uniform sphere is $G M / r^{2}$ towards the center.

There’s a further bonus: since we found this result be adding uniform spherical shells, it is still true if the shells have different densities, provided the density of each shell is the same in all directions. The inner shells could be much denser than the outer ones $—$ as in fact is the case for the Earth.

Field Inside a Spherical Shell

This turns out to be surprisingly simple! We imagine the shell to be very thin, with a mass density $ρ$ kg per square meter of surface. Begin by drawing a two-way cone radiating out from the point $P,$ so that it includes two small areas of the shell on opposite sides: these two areas will exert gravitational attraction on a mass at $P$ in opposite directions. It turns out that they exactly cancel.

This is because the ratio of the areas $A_{1}$ and $A_{2}$ at distances $r_{1}$ and $r_{2}$ are given by $A_{1} / A_{2} = r_{1}^{2} / r_{2}^{2} :$ since the cones have the same angle, if one cone has twice the height of the other, its base will have twice the diameter, and therefore four times the area. Since the masses of the bits of the (uniform thickness) shell are proportional to the areas, the ratio of the masses of the two cone bases is also $r_{1}^{2} / r_{2}^{2} .$ But the gravitational attraction at $P$ from these masses goes as $G m / r^{2},$ and that $r^{2}$ term cancels the one in the areas, so the two opposite areas have equal and opposite gravitational forces at $P .$

In fact, the gravitational pull from every small part of the shell is balanced by a part on the opposite side $—$ you just have to construct a lot of cones going through $P$ to see this. (There is one slightly tricky point $—$ the line from $P$ to the sphere’s surface will in general cut the surface at an angle. However, it will cut the opposite bit of sphere at the same angle, because any line passing through a sphere hits the two surfaces at the same angle, so the effects balance, and the base areas of the two opposite small cones are still in the ratio of the squares of the distances $r_{1}, r_{2} .$

Field Inside a Sphere: How Does g Vary on Going Down a Mine?

This is a practical application of the results for shells. On going down a mine, if we imagine the Earth to be made up of shells, we will be inside a shell of thickness equal to the depth of the mine, so will feel no net gravity from that part of the Earth. However, we will be closer to the remaining shells, so the force from them will be intensified.

Suppose we descend from the Earth’s radius $r_{E}$ to a point distance $r$ from the center of the Earth. What fraction of the Earth’s mass is still attracting us towards the center? Let’s make life simple for now and assume the Earth’s density is uniform, call it $ρ$ kg per cubic meter.

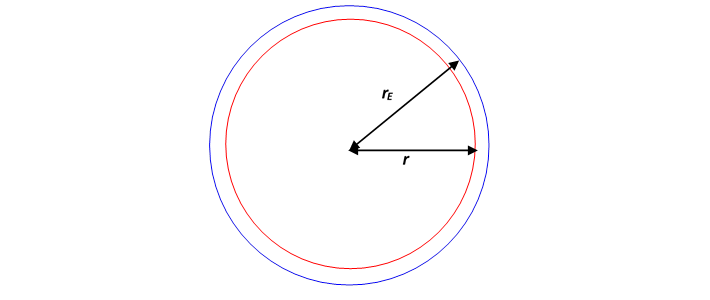
Then the fraction of the Earth’s mass that is still attracting us (because it’s closer to the center than we are $—$ inside the red sphere in the diagram) is $V_{r e d} / V_{b l u e} = \frac{4}{3} π r^{3} / \frac{4}{3} π r_{E}^{3} = r^{3} / r_{E}^{3} .$ .

The gravitational attraction from this mass at the bottom of the mine, distance $r$ from the center of the Earth, is proportional to mass $/ r^{2} .$ We have just seen that the mass is itself proportional to $r^{3},$ so the actual gravitational force felt must be proportional to $r^{3} / r^{2} = r .$ .

That is to say, the gravitational force on going down inside the Earth is linearly proportional to distance from the center. Since we already know that the gravitational force on a mass $m$ at the Earth’s surface $r = r_{E}$ is $m g,$ it follows immediately that in the mine the gravitational force must be

$F = m g r / r_{E} .$ .

So there’s no force at all at the center of the Earth $—$ as we would expect, the masses are attracting equally in all directions.

previous index next