Gravitational Potential Energy
Preliminary Remark
In analyzing the motion of the planets in orbit around the
Sun, we have used Newton’s Law of Gravity ![]() , r being of course the distance between the centers
of the bodies in question. In fact,
though, the precise statement of Newton’s law is that
, r being of course the distance between the centers
of the bodies in question. In fact,
though, the precise statement of Newton’s law is that ![]() where m1, m2 are masses
having infinitesimally small spatial extent, and the total gravitational
attraction between two larger bodies must be found by taking the larger bodies
to be each made up of a very large number of small bodies, then summing over
all the attractive forces between the sets of smaller bodies. In other words,
mathematically speaking, we must integrate over all the tiny masses
making up both bodies.
where m1, m2 are masses
having infinitesimally small spatial extent, and the total gravitational
attraction between two larger bodies must be found by taking the larger bodies
to be each made up of a very large number of small bodies, then summing over
all the attractive forces between the sets of smaller bodies. In other words,
mathematically speaking, we must integrate over all the tiny masses
making up both bodies.
Actually, this is not as bad as it sounds. For the Sun and the Earth, for example, both bodies are very small compared to the distance between them, so taking in account the finite sizes only yields a small correction. But what about the gravitational attraction of the Earth on someone standing on its surface? If we mentally divide the Earth into many parts, it is not at all obvious that the total gravitational force will be the same as if all the Earth’s mass were at one point at the center. Yet that is what Newton concluded when he compared the high flying cannonball with the Moon in orbit, and announced a universal inverse-square law for gravity. And, in fact, Newton was able to prove, using the calculus he invented for the purpose, that a spherically symmetric mass distribution does indeed have the same gravitational attraction for an external object as would an equivalent point mass at the center. We’ll look at the proof later.
Bottom line: Newton established that outside of a spherically symmetric mass distribution, the gravitational field is the same as if all the mass were concentrated in one point at the center.
Gravitational Potential Energy Near the Earth
We first briefly review the familiar subject of
gravitational potential energy near the Earth’s surface, such as in a
room. The gravitational force is of
course ![]() vertically downwards.
vertically downwards.
To raise a mass m, we must apply an upward force ![]() , balancing gravity, so the net force on the body is zero and
it can move upwards at a steady speed (ignoring air resistance, of course, and
assuming we gave it a tiny extra push to get it going).
, balancing gravity, so the net force on the body is zero and
it can move upwards at a steady speed (ignoring air resistance, of course, and
assuming we gave it a tiny extra push to get it going).
Applying the steady force ![]() as the mass moves a small distance
as the mass moves a small distance ![]() takes work
takes work ![]() , and to raise the mass m through a height h
takes work mgh. This
energy is stored and then, when the object falls, released as kinetic
energy. For this reason it is called potential
energy, being “potential kinetic energy”, and written
, and to raise the mass m through a height h
takes work mgh. This
energy is stored and then, when the object falls, released as kinetic
energy. For this reason it is called potential
energy, being “potential kinetic energy”, and written
![]()
Note one obvious ambiguity in the definition of potential energy: do we measure h from the floor, from the top of our workbench, or what? That depends on how far we will allow the raised object to fall and convert its potential energy to kinetic energy—but the main point is it doesn’t matter where we set the zero, the quantity of physical interest is always a difference of potential energies between two heights—that’s how much kinetic energy is released when it falls from one height to the other. (Perhaps we should mention that some of this potential energy may go to another form of energy when the object falls—if there is substantial air resistance, for example, some could end up eventually as heat. We shall ignore that possibility for now.)
Onward and Upward
Let’s now consider the work involved in lifting something so high that the Earth’s gravitational pull becomes noticeably weaker.
It will still be true that lifting through ![]() takes work
takes work ![]() , but now
, but now ![]() , downwards.
, downwards.
So
![]()
and to find the total work needed to lift a mass m from the Earth’s surface (rE from the center of the Earth) to a point distance r from the center we need to do an integral:
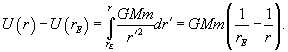
Let’s first check that this makes sense close to the Earth’s surface, that is, in a room. For this case,
![]()
Therefore we can write

where the only approximation is to replace rE + h by rE in the denominator, giving an error of order h/rE, parts per million for an ordinary room.
To see what this potential function looks like on a larger scale, going far from the Earth, it is necessary first to decide where it is most natural to set it equal to zero. The standard convention is to set the potential energy equal to zero at r = infinity! The reason is that if two bodies are very far from each other, they have no influence on each other’s movements, so it is pointless to include a term in their total energy which depends on their mutual interaction.
Taking the potential energy zero at infinity gives the simple form
![]()
we plot it below with r in units of Earth radii. The energy units are GMm/rE, the -1 at the far left being at the Earth’s surface (r = 1), and the first steep almost linear part corresponds to mgh.
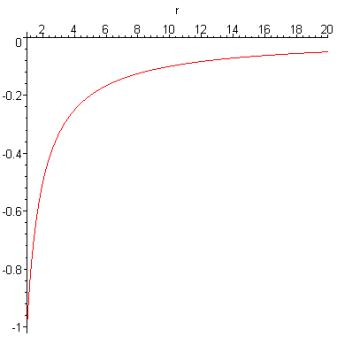
The above is a map of the potential energy “hill” to be climbed in going away from the Earth vertically upwards from any point. To gain a more three-dimensional perspective, the Earth can be visualized as being at the bottom of a “potential well” with flared sides, like this:
Or, from a different perspective: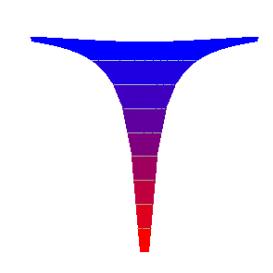
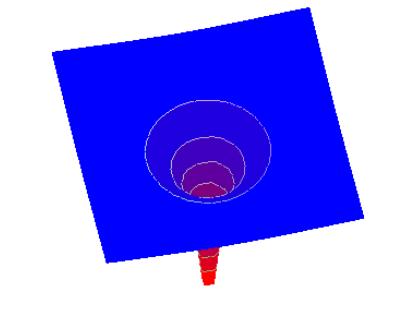
These are of course abstract maps of gravitational potential energy as a function of position, but with this representation our ordinary intuition of climbing hills can be of some use in understanding how moving objects behave in this gravitational field.
Escape!
How fast must a rocket be moving as it escapes the atmosphere for it to escape entirely from the Earth’s gravitational field? This is the famous escape velocity, and, neglecting the depth of the atmosphere, it clearly needs sufficient initial kinetic energy to climb all the way up the hill,
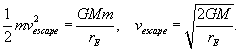
This works out to be about 11.2 km per sec. For the Moon, escape velocity is only 2.3 km per second, and this is the reason the Moon has no atmosphere: if it had one initially, the Sun’s heat would have been sufficient to give the molecules enough thermal kinetic energy to escape. In an atmosphere in thermal equilibrium, all the molecules have on average the same kinetic energy. This means lighter molecules on average move faster. On Earth, any hydrogen or helium in the atmosphere would eventually escape for the same reason.
Potential and Kinetic Energy in a Circular Orbit
The equation of motion for a satellite in a circular orbit is
![]()
It follows immediately that
the kinetic energy ![]() , that is, the Kinetic Energy = -1/2 (Potential Energy) so
the total energy in a circular orbit is half the potential energy. The satellite’s motion can be visualized as
circling around trapped in the circular potential well pictured above. How fast does move? It is easy to check that
, that is, the Kinetic Energy = -1/2 (Potential Energy) so
the total energy in a circular orbit is half the potential energy. The satellite’s motion can be visualized as
circling around trapped in the circular potential well pictured above. How fast does move? It is easy to check that
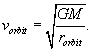
Notice that the escape velocity from the radius of the orbit is just Ö2 times the orbital velocity: this isn’t surprising, because increasing the speed by Ö2 doubles the kinetic energy, which would then be just equal to the potential energy, and enough to get the satellite out of the “well”.
Bottom line: the total energy of a planet of mass m in a circular orbit of radius r about a Sun of mass M is
![]()
Total Energy in an Elliptical Orbit
Remarkably, it turns out that for a planet in an elliptical orbit, the total energy, like the time for one orbit, only depends on the semimajor axis:
![]()
You do not need to be able to prove this, but in case you’re curious, here it is (and, you can skip this!).
Suppose in the elliptical orbit the distance of closest approach is r1, and the speed at that point is v1. the furthest point is labeled r2, the speed there is v2.
Conservation of angular momentum tells us that
r1v1 = r2v2 = L.
Conservation of energy gives:
![]()
which we write
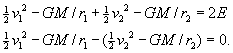
Putting v1 = L/r1,
v2 = L/r2 in the second of these
equations gives us L2 in terms of r1, r2:
![]()
The same substitution in the first equation gives
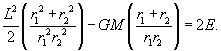
Now substitute the expression for L2 in terms of r1, r2 to give E in terms of r1, r2. You will find
![]()
where a is the semimajor axis.
Different Kinds of Orbits
Imagining the satellite as a particle sliding around in a frictionless well representing the potential energy as pictured above, one can see how both circular and elliptical orbits might occur.
(Optional: More formally, we solved the equation of motion in the previous lecture to find
![]()
which is equivalent to the equation for an ellipse
![]()
as we discussed.)
However, that is not the whole story: what if a rogue planet comes flying towards the Solar System from outer space? What kind of orbit will it follow as it encounters the Sun’s gravity? In fact, our analysis of the equations of motion is equally valid in this case, and the (r,q ) equation is the same as that above! The new wrinkle is that e, which is always less than one for an ellipse, becomes greater than one, and this means that for some angles r can be infinite (the right-hand side of the above equation can be zero). The orbit is a hyperbola: the rogue comes in almost along a straight line at large distances, the Sun’s gravity causes it to deviate, it swings around the Sun, then recedes tending to another straight line path as it leaves the System.