Physics 152: Gravity Homework (and
some Exam) Problems
Michael Fowler 6/1/07
1. Warm-up
exercise: deriving acceleration in circular motion from Pythagoras’ theorem.
Imagine a cannon on a high mountain shoots a cannonball horizontally above the atmosphere at the right speed for it to go in a circular orbit. In one second, the ball will fall 5 meters below a horizontal line, at the same time traveling v meters horizontally, as in the diagram below (where the distances traveled are grossly exaggerated to make clear what’s going on).
Apply Pythagoras’ theorem to the right-angled triangle to
establish that the appropriate speed for a circular orbit just above the
earth’s atmosphere is given by ![]()
(Use the approximation that the distance traveled in one second is tiny compared to the radius of the earth.)

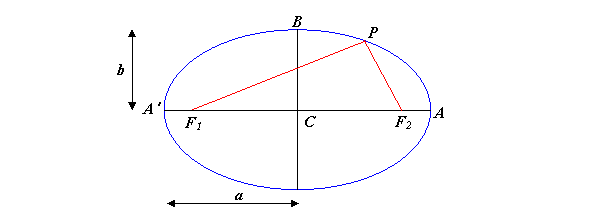
2. Properties
of the Ellipse.
Take a point ![]() on the ellipse very
close to P, and draw lines from the
new point to the two foci.
on the ellipse very
close to P, and draw lines from the
new point to the two foci.
Use the fact that the “rope” is the same length for P, ![]() to prove that a light
ray from one focus to P will be
reflected to the other focus.
to prove that a light
ray from one focus to P will be
reflected to the other focus.
3. Kepler’s Third
Law states that ![]() has the same numerical
value for all the sun’s planets.
has the same numerical
value for all the sun’s planets.
For circular orbits, how are R, T related if the gravitational force is proportional to 1/R? to 1/R3? To R? What can we conclude from Kepler’s Third Law about the gravitational force?
4. Television signals are relayed by synchronous
satellites, placed in orbits such that they hover above the same spot on
Earth. Use Kepler’s Laws and data about
the Moon’s orbit to find how far above the Earth’s surface the synchronous
satellites are. Could one be placed
directly above
5. An evil genius puts a spherical rock (made of ordinary stone) in the earth’s orbit, but moving around the sun the other way. It collides with the earth, landing in the desert. It is estimated that the crater is about the same as would have been caused by a one-megaton hydrogen bomb. How big was the rock?
6. Halley’s comet follows an elliptical orbit, its closest approach to the Sun is observed to be 0.587AU. Given that the orbital period is 76 years, what is its furthest distance from the Sun? What is the ellipticity of this orbit?
7. Halley’s Comet simplified.
(a) A comet having a period of 64 years has closest approach to the Sun 0.5 AU. Use Kepler’s Third Law, and comparison with the Earth, to figure out its farthest distance from the Sun.
(b) What is the ratio of its kinetic energy when nearest to the Sun to its kinetic energy at the farthest point?
(c) How does its kinetic energy at the closest approach to the Sun compare with that of an equal mass in a circular orbit around the Sun at that distance? (An approximate answer will do.)
8. Galileo discovered four satellites of Jupiter:
|
Satellite |
Orbital
Radius in 106 km |
Orbital
Period in Days |
|
Io |
0.422 |
1.77 |
|
Europa |
0.671 |
3.55 |
|
Ganymede |
1.070 |
7.16 |
|
Callisto |
1.880 |
16.7 |
The orbits are all very close to circular.
(Data from http://www.ifa.hawaii.edu/~sheppard/satellites/jupsatdata.html , where 59 other satellites of Jupiter are listed!)
Check that Kepler’s Third Law is satisfied in this system, and use these data to find the mass of Jupiter.
9. The galaxy NGC 4258 contains a disk of matter, like a huge version of Saturn’s rings. The disk is not rigid, but is made up of rocks, etc., all going in approximately circular orbits. The disk has inner radius 0.14 pc (parsec), outer radius 0.28 pc. The inmost part is orbiting with a period of 800 yrs, the outer edge with a period of 2200 yrs.
(a) Show that these data indicate the disk is in a gravitational field dominated by a central massive object (rather than, say, the field of the disk itself).
(b) Find the approximate mass of the central object. The densest known star cluster is about 105 solar masses/pc3. Could the central object be a star cluster? If not, what?
10. Plotting the Gravitational Field.
The diagram below shows how to find the gravitational force at a particular point from a system of two masses.
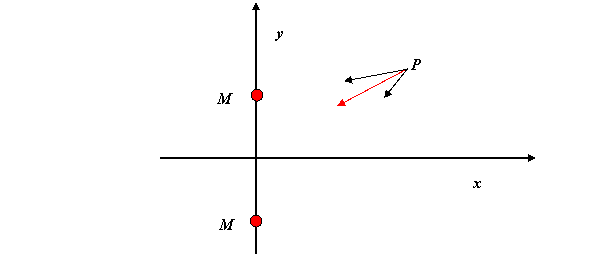
(a) Draw the field vector at several other points, then construct a picture of the field by drawing field lines: continuous lines which at each point are in the direction of the field at that point. (The same as “lines of force” in magnetism.)
(b) Draw the field line diagram for two unequal masses, such as the Earth and the Moon. In particular, make clear how the field behaves along the direct line from the Earth to the Moon.
11. (a) Give a brief explanation, with a diagram, of why the gravitational field inside a uniform spherical shell of matter is zero.
(b) Suppose a very deep tunnel is drilled vertically down. What is the gravitational force felt by a mass of 1 kg in the tunnel at a distance r from the center of the earth, given that it is 10 Newtons at distance RE = 6400 km., that is, at the earth’s surface? (Assume the Earth’s density is uniform.)
* The rest of this
question requires knowledge of Simple Harmonic Motion.
(c) Now suppose in a massive engineering project the tunnel
is drilled in a straight line through the center of the earth and reemerges
near
(d) Suppose there is an asteroid of 64 km radius, made of material with the same density as the earth. If an exactly similar tunnel is drilled through this asteroid, how long would it take a package to “fall” from one end to the other?
12. In the year 3000, a group of bad guys fond of living in caves have excavated a huge spherical cave inside the Moon. (But it’s not centered at the center of the Moon!) Assuming the Moon is a sphere of rock of uniform density, prove that the gravitational field inside the cave is the same everywhere. (Hint: figure out the field for Moon with no cave, then think of the cave as a uniform sphere of negative mass density, and add the two contributions.)
13. Imagine a tunnel bored straight through the Earth
emerging at the opposite side of the globe.
The gravitational force on a mass m
in the tunnel is ![]() .
.
(a) Find
an expression for the gravitational potential
in the tunnel. Take it to be zero at the
center of the Earth.
(b) Now
sketch a graph of the potential as a function of distance from the Earth’s
center, beginning at the center but continuing beyond the Earth’s radius to a
point far away. This curve must be
continuous.
(c) Conventionally, the potential energy is defined by requiring it to be zero at infinity. How would you adjust your answer to give this result?
14. Draw a plot of the gravitational potential along a straight line from the surface of the Earth to the surface of the Moon. What is the minimum speed of a rocket fired directly from the Earth to the Moon to reach it? What speed will it be moving on reaching the Moon’s surface? (Ignore the Earth’s rotation and the Moon’s orbital speed—just consider two fixed masses.)
15. For this question, take the mass of Mars to
be 0.1 Earth masses, and the radius of Mars to be 0.5 Earth radii.
(a) Given that g = 10 m/sec2 at the Earth’s surface, what is the acceleration due to gravity at the surface of Mars? (Show your working.)
(b) A satellite in low Earth orbit travels at 8 km/sec. Use the value of g on Mars you found in part (a) to work out how fast a satellite in a low Mars orbit will travel.
(c) Calculate the escape velocity from Mars.
(d) A synchronous satellite is in a circular orbit (around the Earth) with radius 42,000 km. It happens that the length of a Martian day is close to 24 hours. What would be the orbit radius of a synchronous satellite circling Mars?
16. Phobos, a satellite of Mars, has a radius of 11 km and a mass of 1016 kg. It’s a bit lumpy, but let’s assume it’s spherical to get a doable problem.
(a) What is g on Phobos?
(b) If you can jump to a height of one meter on earth, how high could you jump on Phobos? (Think carefully about this.)
(c) Could an astronaut on a bicycle reach orbital speed on Phobos? (Guesses don’t count, I need to see a derivation). What about reaching escape velocity?
17. Uranus has a radius four times Earth’s radius, but gravity at the surface is only 0.8gearth. Escape velocity from Earth is 11.2 km/sec. Using these facts, and nothing else, find the escape velocity from Uranus.
18. (a) Find the orbital speed of a spaceship in low orbit around the Moon, just skimming the mountain tops.
(b) Suppose the pilot suddenly increases the speed
by a factor of ![]() , but during the brief acceleration keeps the spaceship
pointing the same way, that is, horizontally.
Describe the path the spaceship will take after the engine cuts out—does
this curve have a name?.
, but during the brief acceleration keeps the spaceship
pointing the same way, that is, horizontally.
Describe the path the spaceship will take after the engine cuts out—does
this curve have a name?.
19. In deep space, an astronaut is marooned ten meters from his four-ton spacecraft. If he is exactly at rest relative to the craft, and there are no other gravitational fields close by, estimate how long it will be before he’s back on board. How fast will he be moving when he hits the craft (which is 5 meters in diameter)?
20. The escape speed from the moon is 2.38 km/sec. Suppose you had on the moon a cannon that could fire shells at 2.4 km/sec. Obviously, if you fired a shell vertically upwards, it would escape the moon’s gravity. But what if you fired it almost horizontally, just elevated enough so it cleared the mountains? Describe its trajectory in this situation.
21. The escape velocity from Earth is 11.2 km./sec. What is the escape velocity from the Solar System starting in a high parking orbit several Earth radii from Earth. (Hint: what is the Earth’s speed in orbit?) On the basis of this, estimate roughly how much more fuel energy is needed to reach the outer planets compared with going to the Moon. Is there a way around this problem?
22. Imagine a fictitious moon, which we’ll call Moon1, a sphere with the same density as the earth, but with radius exactly one-quarter the earth’s radius:
rMoon1 = rearth, RMoon1=0.25Rearth.
(a) Taking the acceleration due to gravity gearth to be 10 m.sec-2 at the earth’s surface, what is the acceleration gMoon1 due to Moon1’s gravity at Moon1’s surface?
(b) If the escape velocity from the earth’s surface is 11 km.sec-1, what is the escape velocity from Moon1’s surface?
(c) If it takes 90 minutes for a satellite in low earth orbit (orbit radius approximately equal to earth radius) to go around once, how long will it take a satellite in a low Moon1 orbit (skimming the surface of the airless moon) to go around once?
(d) The real Moon has a radius close to that of Moon1 above (our Moon’s radius is 10% bigger than one-quarter the earth’s, we’ll neglect that difference here). However, the real Moon has a density only 60% that of the earth. In this part, use the real Moon’s density (but Moon1’s radius) to recalculate the answers to (a), (b) and (c) above.
23. Saturn’s satellite Titan has an orbit of radius 1.22 x 106 km., and a period of 15.9 days. Use this information to find the mass of Saturn, then use its radius of 60,300 km to deduce
(a) Saturn’s average density
(b) the value of g at the surface of Saturn
(c) the escape velocity from Saturn.
24. The furthest planet, Pluto, has a radius 20% of the Earth’s radius, and a mass only 0.2% that of the Earth. (Both figures are within about 5%.)
(a) Suppose an astronaut, in full insulated gear, can jump 0.5 m high on Earth. How high can she jump on Pluto? (You don’t need to know G to answer this!)
(b) Assuming “air” resistance is negligible, what speed would a (rocket driven) car racing over a flat plane (a frozen sea) on Pluto need to be traveling to attain escape velocity? (Escape velocity from Earth is 11.2 km per sec: use this fact.)
(c) Would it in fact have left the ground before reaching that speed? Explain your answer.
25. The escape velocity from a certain planet is 10 km per sec. The planet has a moon having radius one-quarter that of the planet, and density one-half that of the planet. What is the escape velocity from the planet’s moon?
26. In an imaginary universe, the gravitational force decreases with distance as 1/R instead of 1/R2. Suppose in that universe there is a planet the same size as Earth and also having the same value of g near the surface. Would the period of a satellite in low circular orbit (just above an atmosphere of negligible depth) be the same? Would the escape velocity be the same?
*27. Somewhere on the line from the Earth to the
Sun there is a point, called a Lagrange point, such that a satellite placed
there will orbit around the Sun in sync with the Earth. In fact, there’s already a satellite there,
it monitors the Sun continuously. Come
up with some estimate of how far from Earth this Lagrange point is (the Web
might be helpful). ![]()
28. On a Moon mission, a spaceship is fired from Earth with just enough speed to reach the Moon, but aimed so that it just misses the Moon, and loops behind it, closest approach being near the point on the Moon’s surface furthest from Earth. At that point, a small distance above the Moon’s surface, the ship fires a rocket to put it into low circular orbit around the Moon. What is (approximately) the change in speed needed for this maneuver?
Elliptic Paths to Planets and Asteroids
29. The asteroid Gaspra is twice as far from the sun as we are. Assume it is in a circular orbit, and you are planning an expedition there.
The most economical trajectory is along an elliptical orbit, whose closest approach to the
sun, call it r1, is at the earth’s orbit, and furthest distance from the sun, r2, is at Gaspra’s orbit.
Suppose that after leaving the atmosphere, the spaceship is rapidly speeded up to v1, then the engines cut out, and it follows the assigned elliptic path, arriving at Gaspra’s orbit with speed v2. (Neglect the earth’s gravitational pull on the spaceship.)
(a) What quantities are conserved on the elliptic orbit?
(b) Find two equations for v1, v2 in terms of r1, r2 and GM, where M is the mass of the sun.
(c) Solve the two equations to find v1.
(d) Find the speed of the earth in orbit in terms of r1 and GM.
(e) Given that the earth’s speed in orbit is 30 km per sec, how much does the spaceship need to be speeded up relative to the earth to get to Gaspra along this ellipse?
(f) Show on a diagram the earth in orbit, and the direction in which the spaceship needs to be moving just after leaving the earth to reach Gaspra. Approximately, what path would the spaceship take if fired in the opposite direction?
30. Suppose we are sending a space probe of mass m from Earth to Jupiter by the most economical elliptical route. Take the radius of Jupiter’s orbit around the sun to be 5 AU.
(a) What is the total energy of the probe in the elliptical orbit?
(b) Assume it is fired from a parking orbit circling the earth far above, so the earth’s own gravity has a negligible effect. Given that the earth moves in orbit at 30 km/sec, what is the speed of the probe relative to earth as it enters the elliptical orbit?
(c) What is its speed when it reaches Jupiter’s orbit?
31. We plan to send a probe to an asteroid which has a circular orbit of radius three times that of the earth’s orbit (assumed also circular).
(a) Sketch the most efficient path, showing on your diagram the earth’s orbit and the asteroid’s.
(b) If the earth travels in its orbit at 30 km per sec, at what speed relative to the earth must the probe be moving after it has cleared essentially all the earth’s gravitational field?
32. Suppose a satellite is in low earth orbit, that is, in a circular orbit at a height of 200 km., so the radius of the circle is 6600 km., say. We want to raise it to a circular orbit of twice that radius (so it will now be going in a circle at a height of 6800 km above the earth’s surface.)
The technique is to give it two quick boosts: boost1 puts it into an elliptical orbit, where its furthest point from the earth’s center is exactly twice its distance of closest approach, boost2, delivered at the topmost point of the orbit, transfers it to a circular orbit at that radius.
Use conservation of angular momentum and energy in the elliptical orbit to answer these two questions:
(a) By what percentage did boost1 increase its speed?
(b) By what percentage did boost2 increase its speed?
(b) Give a qualitative explanation of how you would fire a rocket to get back to Earth from a parking orbit near Mars (so you neglect Mars’ own gravity).
33. A “Binary” System.
A very recently discovered “earthlike” planet—we’ll call it P—orbits the red dwarf star Gleise 581, which is 20 light years from us.
P’s sun (Gleise 581) has a mass one-third the mass of our sun.
The planet P’s presence was established by detecting a wobble in the motion of Gleise 581 with a period of 13 days. (The wobble being caused by the orbiting planet’s gravity: think binary system.)
(3) (a) How far is P from its sun?
Do this as follows:
for any solar type system with circular planetary orbits ![]() , M being the mass
of that sun.
, M being the mass
of that sun.
Use as units earth years
and A.U. (distance of Earth from Sun), so for our solar system in these units ![]() .
.
What is ![]() in the same units (earth years and earth A.U.’s) in the Gleise 581 system?
in the same units (earth years and earth A.U.’s) in the Gleise 581 system?
The wobble means P orbits its sun once in 13 days. Write that in earth years, and deduce how far P is from its sun, in A.U.
(b) Given that 1 A.U = 1.5x 108 km, how fast is P moving in its (assumed circular) orbit?
(c) From detecting the Doppler shift, it is found that the maximum speed of the sun Gleise 581 in its 13-day wobble is 3 m/sec. From this, thinking of the planet P and the sun Gleise 581 as a “binary star” system, what is the ratio of the planet P mass to the sun (Gleise) mass?
(d) Our sun’s mass is about 300,000 earth masses. How does the “earthlike” planet P’s mass compare with the earth’s mass? (Recall Gleise has a mass one-third of our sun’s mass.)
General Relativity
34. (a) State the Equivalence Principle.
(b) Explain how shining light across an elevator can lead to the conclusion that light is deflected by gravity. (Include a diagram.)
(c) Given that light is deflected of order 1 second of arc on passing by the sun, and that the order of magnitude is correctly given by a simple classical approximation, how much would you estimate light to be deflected (order of magnitude) passing the surface of a neutron star, having twice the mass of the Sun and a radius of 10 km (the sun’s radius being 700,000 km)? State what approximations you’re making.
35. The first experimental test of General Relativity was an observation of the deflection of starlight by the Sun’s gravitational field (observed during a Solar eclipse). Classically, regarding light as tiny particles, the deflection can be estimated within 20% or so by approximating the Sun’s gravitational effect as equal to gravity at the Sun’s surface acting for a period of time equal to that needed for the particles to travel a distance equal to the Sun’s diameter. Calculate what angular deflection that would give, in seconds of arc. General Relativity predicts that the actual deflection should be twice the classical value—and that was observed.
36. The GPS satellites are at an altitude of about 20,000 km. Find their speed, and figure out the necessary correction factors for their clocks from both Special and General Relativistic effects. Are these corrections important for the functioning of the system, or can they be neglected in practice?
Miscellaneous
37. At http://www.enchantedlearning.com/subjects/astronomy/activities/coloring/Solarsystem.shtml you will find the following image:
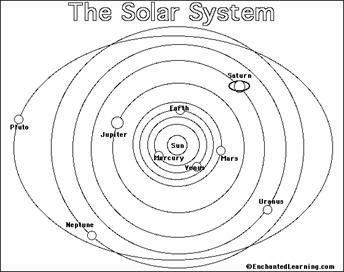
What’s wrong with the orbit of Pluto as shown here?
38. Mercury can be observed as a small black dot crossing the face of the Sun, this occurs about every ten years on average. Since Mercury goes around in 88 days, why is this so rare? Also, it only ever happens in May or November. How would you explain this pattern?
39. Some future explorer decides to fly by a neutron star, following a free-fall trajectory in which the spaceship loops behind the neutron star and comes back—so within the spaceship, the astronaut will be “weightless”. However, if g varies significantly between the head and foot of the astronaut, this could have disastrous consequences.
(a) Estimate at what rate of variation of g the astronaut is unsafe.
(b) Assume the neutron star has a mass of two solar masses, and a radius of 10 km. How close to the surface is it safe for the ship to approach?
40. The asteroid Icarus was only four million miles from earth on a recent pass. If a collision took place, and Icarus fell to earth, give a ballpark estimate of the energy released in the inelastic collision. Compare it with a one megaton hydrogen bomb.
Flashlet and Applet Exercises
41. (a) Activate the Mars trip flashlet. The initial launch speed you enter is from a high parking orbit (say at ten Earth radii) so that the Earth’s own gravitational field has negligible effect. Find the minimum speed needed to reach Mars, sketch a picture of this most economical orbit, and estimate how long the trip would take.
(b) Give a qualitative explanation of how you would fire a rocket to get back to Earth from a parking orbit near Mars (so you neglect Mars’ own gravity).
42. (a) From the Fact Sheet, find the speed of Jupiter in orbit.
(b) Open the Jupiter slingshot flashlet. Note that you can adjust both the initial speed of the rocket approaching Jupiter, and how closely you begin to Jupiter’s orbit. Imagine your rocket barely makes it out to Jupiter’s orbit, so has no speed left—but you’ve perfectly timed it to derive maximum benefit from the slingshot effect. Could Jupiter give it enough of a boost to get it thrown out of the solar system? Justify your answer: what does the rocket’s orbit look like as seen by someone on Jupiter?
43. Open the Newtonian
Mountain applet. The height of the
mountain (
(a) Experiment with the applet to find the speed at the top of an ICBM trajectory compared with speed in a circular orbit at the same height.
(b) If the ICBM is launched with an engine that cuts out as it leaves the atmosphere, what is the approximate speed as the engine cuts out? (Answer in km/sec – I apologize for the applet being in mph. Take the radius of the Earth to be 6400 km., and neglect the thickness of the atmosphere.)
(c) When the engine cuts out, what is the angle between the trajectory and the horizontal?
(Hint: use conservation of angular momentum.)