Heat: the Essentials
Heat, Temperature, Specific Heat, Work
The first thermometer (Galileo’s) used expansion of gas with temperature: it wasn’t reliable because it failed to allow for atmospheric pressure variation.
Mercury in glass became the standard, and made possible the discovery of the
Zeroth Law of Thermodynamics: If two objects are in thermal equilibrium with a third, then they are in thermal equilibrium with each other. (The “third body” in a practical situation being the thermometer.)
The unit of heat: 1 calorie is the heat required to raise the
temperature of 1 gram of water by 1 degree Celsius.
BUT the Calories labeling food items are KILOcalories:
enough to heat one kilogram of water through one degree!
The specific heat
of a substance is the heat required in calories to raise the temperature of 1
gram by 1 degree Celsius.
And, you must be able to use this to solve
simple calorimetric problems: finding specific heat of a sample (as we did in
class) by immersing it in boiling water for a while, then transferring it to
some cold water at a known temperature and finding the change in cold water
temperature.
Be aware of the result of Dulong and Petit, that for a whole series of
elements the product of atomic weight and specific heat was the same,
and its significance in terms of heat capacity per atom.
Latent heat: know what it is.
Coefficients of expansion: know the ballpark value for metals, be able to
prove that the volume coefficient is three times the linear, and know that
water contracts on heating for a few
degrees above freezing.
Know how pressure varies
with temperature for most gases, and how that leads to a natural temperature
scale, and, putting that together with Boyle’s Law, we get the Gas Law PV = nRT.
You should know what a
mole of gas is, what Avogadro’s number means,
and approximately what it is.
Know that the Caloric Theory, treating heat as a fluid
like electricity, gives accurate predictions for any problem involving heat
flow between or within bodies, and only fails
when heat is converted to work or work to heat, and that when heat is
converted to work, total energy is
conserved: in other words, the amount of work done equals the amount of heat
that has disappeared, the unit equivalence being that 1 calorie = 4.2 Joules
approximately: and in doing conversions beware
of confusing calories with kilocalories!
This is the:
First Law of Thermodynamics: Total Energy (including heat
energy) is conserved.
Kinetic Theory of Gases
Be able to derive 
from a molecule
bouncing between top and bottom of a box, and put this together with the Gas
Law 
and Boltzmann’s
constant 
to connect temperature with molecular kinetic
energy:
Understand velocity
space in describing the instantaneous state of a gas. Know that the distribution of molecular
speeds 
, be able to sketch it
(very approximately, where is
its maximum value?) and have some idea how it changes with temperature.
Understand from the Gas Law why 
Degrees of freedom of a molecule: translational (that is, just moving in a direction), rotational, possibly vibrational.
Ideal Gas Thermodynamics: Specific Heats,
Isotherms, Adiabats
For a monatomic gas (no
rotational energy) 
Hence
.
Be able to derive
Mayer’s relationship 
Know that 
, have some idea why, and know the definition of γ:
PV Graphs and Heat Engines
The properties of a fixed amount of an ideal gas are completely defined by P and V, since T follows from the Gas Law. A cylinder containing a gas close to ideal is the central mechanism in almost all heat engines. The flow of heat energy into mechanical energy is analyzed by tracing the path of the gas in the P, V plane.
The simple graphs have possible segments of the following four kinds:
(Important! these are all best understood by tracking the energy flow.)
1. Isotherms, temperature constant, so internal energy constant. Therefore along an isotherm the work done is exactly equal to the heat absorbed.
2. Adiabats: no
heat exchanged. Therefore, the work done is equal to the change in
internal energy, and for an ideal gas that is just 
.
3. Constant volume: no work done, so heat absorbed = change in internal energy.
4. Constant pressure:
work done = 
The Carnot Cycle
Be able to derive
Know how to sketch the Carnot cycle in the P, V plane, and be able to explain just what’s happening along each leg.
Be able to derive
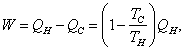
from which
Second Law of Thermodynamics: No
engine can be constructed that works in a cycle, extracts heat from a hot
reservoir, delivers mechanical work, and dumps no waste heat in a cold reservoir.
Understand how this
Law leads to the conclusion that no heat engine can be more efficient than a
Carnot cycle.
Entropy
Know the definition of entropy of an ideal gas in the P, V plane,
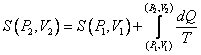
(over a reversible path) and be able to prove it’s the same along all reversible paths.
Third Law of Thermodynamics: A
system at absolute zero temperature has zero entropy.
(This was at first a postulate, a guess, found to be true later using quantum mechanics.)
For a perfect gas:
This means entropy difference depends only on initial and final states, you could go from one to the other irreversibly—the entropy change would still be the same.
Entropy change in a gas expanding into a vacuum:
Entropy as a measure of the number of possible states of a system at a given energy.
Entropy always increases in the real world.