Heat Homework Problems
1. How much higher is the Eiffel tower on the hottest day in the year compared with the coldest night? (You can, of course, find all the info you need using Google.)
2. An old fashioned mercury in glass fever thermometer has a bulb at the end containing say 0.25 ml of mercury. Assume the mercury goes 3 cm further along the tube for a temperature of 104°F compared with 98.6°F, what is the radius of the capillary tube (the thin hollow in the middle of the glass that the mercury goes up? (You need to find the coefficient of expansion of mercury, of course.)
3. A lead bullet is fired into a block of wood at 300 m sec-1. Assume the frictional heating as the bullet is stopped in the wood all goes into heating the bullet (the wood is a fairly good insulator). Does the bullet melt? You’ll need to find its latent heat of melting as well as its specific heat and melting temperature.
4. When Joule was on his honeymoon in
5. A carbon dioxide fire extinguisher holds three liters of compressed carbon dioxide, and weighs 3 kg more when full than when empty. At room temperature (20°C) what is the pressure inside the extinguisher? (Assume the gas obeys the ideal gas law in this range of pressures.)
6. Cass Sackett in our Department can cool a gas of Rubidium atoms into a Bose-Einstein condensate. He tells me this weird phenomenon takes place as the gas cools below 10-7K. What is the average (rms) speed of the atoms at that temperature?
7. In the derivation of the pressure an ideal gas exerts on the sides of a cubical box, gravity was neglected. Now include it: compare the pressure on the top of the box with that on the bottom, thinking in terms of the molecules bouncing back and forth between the top and bottom, but being accelerated by gravity on the way down, and prove that the pressure difference is the same as a simple hydrostatic picture would give. (Take the box to be small, so that the fractional velocity change is small.)
8. If the Calories in a Big Mac could be used with 100% efficiency to raise it vertically, how high would it go? (We write Calorie meaning the energy to raise 1 kg of water by 1°C.)
9. If a cyclist maintains a speed of 10 m sec-1 on level ground, and her muscles can turn chemical energy (Calories) into work with 40% efficiency, how many Calories an hour does she burn? Assume C = 0.35 in the inertial drag formula, but you have to estimate her cross sectional area.
10. In the reactor of a nuclear power plant, water under pressure is heated to 330°C. The plant discharges waste heat into river water at 15°C. The electrical power produced is 1 gigawatt (109 watts). If the plant were an ideal Carnot heat engine, what would be the rate of production of waste heat? Actually, such plants only operate at about 60% of Carnot efficiency—so what is the real waste heat production? Assume now the cooling water from the river runs through at a rate of 40,000 kg/sec. (40 tons of water per second! This is a typical figure.) What is the temperature rise of the cooling water?
(These figures are from:
http://dspace.mit.edu/bitstream/1721.1/35222/1/MIT-EL-79-040-09531570.pdf)
11. (a) Give rough estimates of the fraction of oxygen molecules in the upper atmosphere that are moving at escape velocity or above. (The temperature can reach 1000K.)
(Hint: the only
important factor is 
and in fact since 
this factor can be
written 
where 
is the root mean square velocity at the gas temperature.)
(b) Do the same for any helium atoms in the upper atmosphere. Note that any fraction that contains a significant number of atoms will be big enough for all to escape eventually.
(c) Do the same for hydrogen molecules.
(d) Mars is at about 0°C. Would you expect it to have any atmosphere? What of the common gases would you expect to find, if any? Give reasons.
(e) We know the Moon has no atmosphere—is that consistent with what we know of its gravity and temperature?
12. Joule was the first person to suggest that meteors shone brightly because as they entered the atmosphere, friction converted their kinetic energy to heat. Assuming a meteor is an iron ball, and it enters the earth’s atmosphere at a speed similar to that of the earth’s orbital speed around the sun. Estimate what temperature it might reach. Would it melt?
13.
A Brownian motion problem: recall the Brownian motion arises from a tiny
but visible object, like a grain of pollen, being buffeted about by random hits
from molecules on all sides. Let’s make a simple mathematical model: represent
its path by a sequence of vectors, all of unit length, but each new step is in
a completely random direction. Let’s
call these unit-length vectors 
We’ll
restrict the motion to two dimensions for simplicity. Draw a few sample paths. Using the fact that the direction of each vector
is completely random relative to any other vector, prove that the average
distance traveled after N steps is
proportional to 
.
Hint: consider the square of the distance from the beginning to the end of the N step path, and see what happens to it when you average over all possible step directions for the sequence of steps making up the path.
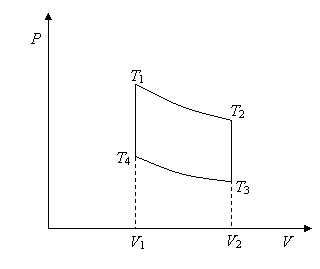14.
A standard gasoline engine is quite well approximated by the Otto cycle, which
has two fixed volume sides, and adiabats top and
bottom.
Heat is absorbed along the 4 to 1 leg, heat is dumped along the 2 to 3 leg. There is of course no heat exchange along the adiabatic legs 1 to 2 and 3 to 4.
(a) Find the heat that goes in and the heat dumped and figure out the efficiency of the engine just from those figures. Your answer should be a function of the four temperatures only.
(b) Find the work the engine does from 1 to 2 in terms of the two temperatures and CV.
(c) Using the equation for an adiabat, find the work done from 1 to 2 in terms of T1, V1, V2. Next, do the same for the work done on the engine from 3 to 4, in terms of T4, V1, V2.
(d) Relate the net work done by the engine in one cycle to the heat input along the 4 to 1 leg to find the efficiency in terms of the two volumes V1, V2 only. The ratio of these two volumes is the compression ratio.