Deriving Kepler’s Laws
from the Inverse-Square Law
For a more recent lecture covering almost all this material, click here. The calculus derivation is near the end.
Preliminaries
Of course, Kepler’s Laws originated from observations of the solar system, but Newton’s great achievement was to establish that they follow mathematically from his Law of Universal Gravitation and his Laws of Motion. We present here a calculus-based derivation of Kepler’s Laws. You should be familiar with the results, but need not worry about the details of the derivation—it’s just here in case you’re curious.
The standard approach in analyzing planetary motion is to use (r, q ) coordinates, where r is the distance from the origin—which we take to be the center of the Sun—and q is the angle between the x-axis and the line from the origin to the point in question.
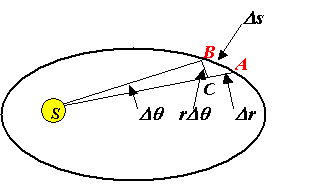
In the picture above, in which I have greatly exaggerated the ellipticity of the orbit, suppose the planet goes from A to B, a distance Ds, in a short time Dt, so its speed in orbit is Ds/Dt. Notice that the velocity can be resolved into vector components in the radial direction Dr/Dt (in this case negative) and in the direction perpendicular to the radius, rDq/Dt. The short line BC in the diagram above is perpendicular to SB (S being the center of the Sun), and therefore becoming perpendicular to SC as well in the limit of AB becoming an infinitesimally small distance.
In the limit of small Ds, then, we have ![]() where the angular
velocity
where the angular
velocity ![]() .
.
Kepler’s Second Law
We shall consider Kepler’s Second Law (that the planet sweeps out equal areas in equal times) first, because it has a simple physical interpretation.
Looking at the above picture, in the time Dt during which the planet moves from A to B, the area swept out is the approximately triangular area ABS, where S is the center of the Sun. For the distance AB sufficiently small, this area tends to that of the long thin triangle BSC, which has a base of length rDq and a height r. Using area of a triangle = ½ base´height, it follows immediately that
![]()
Now, the angular momentum L of the planet in its orbit is given by
![]()
so the rate of sweeping out of area is proportional to the angular momentum, and equal to L/2m.
Newton’s Laws tell us that the rate of change of angular momentum is equal to the torque of the forces acting on the system. For the planet orbiting the Sun, this torque is zero: the only force acting is gravity, and that force acts in a line from the planet towards the center of the Sun, and therefore has zero torque—no leverage—about that central point, so the planet’s angular momentum about that point must remain constant. Consequently, the rate at which area is swept out is also constant, and Kepler’s Second Law follows: equal areas are swept out in equal times.
Ellipses
Before deriving Kepler’s First Law, we’ll review some basic facts about ellipses.

An ellipse is essentially a circle scaled shorter in one direction, in (x, y) coordinates it is described by the equation
![]() ,
,
a circle being given by a = b. The lengths a and b are termed the semimajor axis and the semiminor axis respectively.
An ellipse has two foci, shown F1 and F2 on the diagram, which have the optical property that if a point source of light is placed at F1, and the ellipse is a mirror, it will reflect—and therefore focus—all the light to F2. One way to draw an ellipse is to take a piece of string of length 2a, tie one end to F1 and the other to F2, and hold the string taut with a pencil point. Anywhere this happens on a flat piece of paper is a point on the ellipse. In other words, the ellipse is the set of points P such that PF1 + PF2 = 2a.
The ellipticity of the ellipse e is defined by writing the distance from the center of the ellipse to a focus OF1 = ea.
In fact, in analyzing planetary motion, it is more natural to take the origin of coordinates at the center of the Sun rather than the center of the elliptical orbit. It is also more convenient to take (r, q ) coordinates instead of (x, y) coordinates, because the strength of the gravitational force depends only on r. Therefore, the relevant equation describing a planetary orbit is the (r, q ) equation with the origin at one focus. For an ellipse of semi major axis a and eccentricity e the equation is:
![]() .
.
It is not difficult to prove that this is equivalent to the traditional equation in terms of x, y presented above.
Kepler’s First Law
Note: I’m including the calculus derivation of the elliptic orbit, not to be found in the textbooks, just so you can see that it’s calculus, not magic, that gives this result. This is an optional section, and will not appear on any exams.
We now back up to Kepler’s First Law: proof that the orbit is in fact an ellipse if the gravitational force is inverse square. As usual, we begin with Newton’s Second Law: F = ma, in vector form. The force is GMm/r2 in a radial inward direction. But what is the acceleration? Is it just d2r/dt2? Well, no, because if the planet’s moving in a circular orbit it’s still accelerating inwards at rw2 (same as v2/r) even though r is not changing at all. The total acceleration is the sum, so ma = F becomes:
![]()
This isn’t ready to integrate yet, because w varies too. But since the angular momentum L is constant, L = mr2w, we can get rid of w in the equation to give:
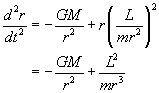
This equation can be integrated, using two very unobvious tricks, figured out by hindsight. The first is to change go from the variable r to its inverse, u = 1/r. The other is to use the constancy of angular momentum to change the variable t to q.
Anyway, ![]() so
so ![]() .
.
Therefore ![]() and similarly
and similarly ![]() .
.
Substituting in the equation of motion gives:
![]()
This equation is easy to solve! The solution is
![]()
where A is a constant of integration, determined by the initial conditions.
This is equivalent to the standard (r, q) equation of an ellipse of semi major axis a and eccentricity e, with the origin at one focus, which is:
![]() .
.
Kepler’s Third Law
The time it takes a planet to make one complete orbit around the Sun T (one planet year) is related to the semi-major axis a of its elliptic orbit by
![]() .
.
We have already shown how this can be proved for circular orbits, however, since we have gone to the trouble of deriving the formula for an elliptic orbit, we add here the(optional) proof for that more general case.
The area of an ellipse is pab, and the rate of sweeping out of area is L/2m, so the time T for a complete orbit is evidently
![]() .
.
Putting the equation
![]() in the standard form
in the standard form ![]() , we find
, we find
![]() .
.
Now, the top point B of the semi-minor axis of the ellipse (see diagram above) must be exactly a from F1 (visualize the string F1BF2), so using Pythagoras’ theorem for the triangle F1OB we find
![]() .
.
Using the two equations above, the square of the orbital time
![]()
We have established, then, that the time for one orbit depends only on the semimajor axis of the orbit: it does not depend on how elliptic the orbit is!