More Gravity
Michael Fowler, UVa 2/4/06
Introduction
Let’s begin with the definition of gravitational field:
The gravitational field at any point P in space is defined as the gravitational force felt by a tiny
unit mass placed at P.
So, to visualize the gravitational field, in this room or on a bigger scale such as the whole Solar System, imagine drawing a vector representing the gravitational force on a one kilogram mass at many different points in space, and seeing how the pattern of these vectors varies from one place to another (in the room, of course, they won’t vary much!)
To build an intuition of what various gravitational fields look like, we’ll examine a sequence of progressively more interesting systems, beginning with a simple point mass and working up to a hollow spherical shell, this last being what we need to understand the Earth’s own gravitational field, both outside and inside the Earth.
Field from a Single Point Mass
This is of course simple: we know this field has strength GM/r2, and points towards the mass—the direction of the attraction. Let’s draw it anyway, or, at least, let’s draw in a few vectors showing its strength at various points:
This is a rather inadequate representation: there’s a lot of blank space, and, besides, the field attracts in three dimensions, there should be vectors pointing at the mass in the air above (and below) the paper. But the picture does convey the general idea.
A different way to represent a field is to draw “field lines”,
curves such that at every point along the curve’s length, its direction is the
direction of the field at that point. Of
course, for our single mass, the field lines add little insight: 
The arrowheads indicate the direction of the force, which points the same way all along the field line. A shortcoming of the field lines picture is that although it can give a good general idea of the field, there is no precise indication of the field’s strength at any point. However, as is evident in the diagram above, there is a clue: where the lines are closer together, the force is stronger. Obviously, we could put in a spoke-like field line anywhere, but if we want to give an indication of field strength, we’d have to have additional lines equally spaced around the mass.
Gravitational Field for Two Masses
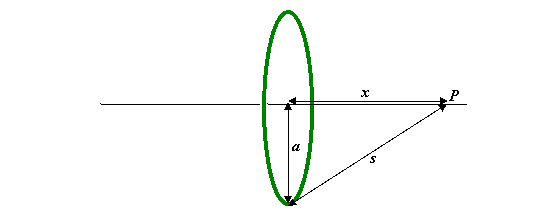
The next simplest case is two equal masses. Let us place them symmetrically above and below the x-axis:
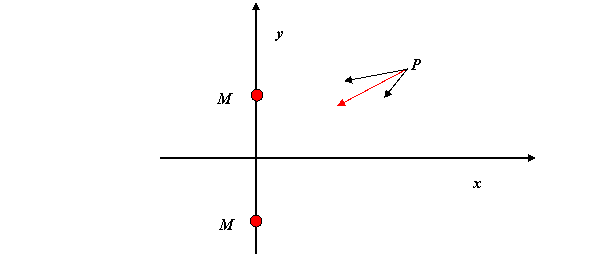
Recall 
. A point mass m = 1 at P will therefore feel gravitational attraction towards both masses M, and a total gravitational field equal to the vector sum of these two forces, illustrated by the red arrow in the
figure.
The Principle of Superposition
The fact that the total gravitational field is just given by adding the two vectors together is called the Principle of Superposition. This may sound really obvious, but in fact it isn’t true for every force found in physics: the strong forces between elementary particles don’t obey this principle, neither do the strong gravitational fields near black holes. But just adding the forces as vectors works fine for gravity almost everywhere away from black holes, and, as you will find later, for electric and magnetic fields too. Finally, superposition works for any number of masses, not just two: the total gravitational field is the vector sum of the gravitational fields from all the individual masses. Newton used this to prove that the gravitational field outside a solid sphere was the same as if all the mass were at the center by imagining the solid sphere to be composed of many small masses—in effect, doing an integral, as we shall discuss in detail later. He also invoked superposition in calculating the orbit of the Moon precisely, taking into account gravity from both the Earth and the Sun.
Exercise: For the two mass case above, sketch the gravitational field vector at some other points: look first on the x-axis, then away from it. What do the field lines look like for this two mass case? Sketch them in the neighborhood of the origin.
Field Strength at a Point Equidistant from the Two Masses
It is not difficult to find an exact expression for the gravitational field strength from the two equal masses at an equidistant point P.
Choose the x,y axes so that the masses lie on the y-axis at (0, a) and (0,-a).
By symmetry, the field at P must point along the x-axis, so all we have to do is compute the strength of the x-component of the gravitational force from one mass, and double it.
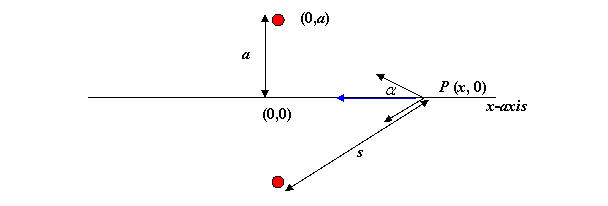
If the distance from the point P to one of the masses is s,
the gravitational force towards that mass has strength 
. This force has a
component along the x-axis equal to 
, where 
is the angle between
the line from P to the mass and the x-axis, so the total gravitational force
on a small unit mass at P is 
directed along the x-axis.
From the diagram, 
, so the force on a unit mass at P from the two masses M is
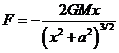
in the x-direction. Note that the force is exactly zero at the origin, and everywhere else it points towards the origin.
Gravitational Field from a Ring of Mass
Now, as long as we look only on the x-axis, this identical formula works for a ring of mass 2M in the y, z plane! It’s just a three-dimensional version of the argument above, and can be visualized by rotating the two-mass diagram above around the x-axis, to give a ring perpendicular to the paper, or by imagining the ring as made up of many beads, and taking the beads in pairs opposite each other.
Bottom line: the field from a ring of total mass M, radius a, at a point P on the axis of the ring distance x from the center of the ring is
.
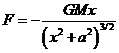*Field Outside a Massive Spherical Shell
This is an optional section: you can safely skip to the result
on the last line. In fact, you will
learn an easy way to derive this result using Gauss’s Theorem when you do
Electricity and Magnetism. I just put
this section in so you can see that this result can be derived by the straightforward, but quite challenging, method of
adding the individual gravitational attractions from all the bits making up the
spherical shell.
What about the gravitational field from a hollow spherical shell of matter? Such a shell can be envisioned as a stack of rings.
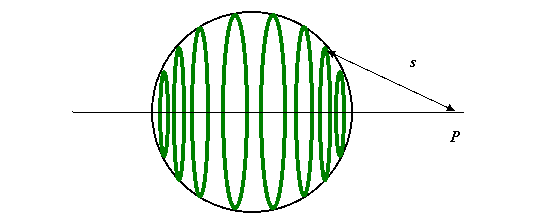
To find the gravitational field at the point P, we just add the contributions from all the rings in the stack.
In other words, we divide the spherical shell into narrow
“zones”: imagine chopping an orange into circular slices by parallel cuts,
perpendicular to the axis—but of course our shell is just the skin of the orange! One such slice gives a ring of skin,
corresponding to the surface area between two latitudes, the two parallel lines
in the diagram above. Notice from the
diagram that this “ring of skin” will have radius 
, therefore circumference 
and breadth 
, where we’re taking 
to be very small. This means that the area of the ring of skin is
.
So, if the shell has mass 
per unit area, this
ring has mass 
, and the gravitational force at P from this ring will be
.
Now, to find the total gravitational force at P from the entire shell we have to add the contributions from each of these
“rings” which, taken together, make up the shell. In other words, we have to integrate the above expression in 
So the gravitational field is:
.
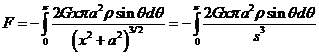In fact, this is quite a tricky integral: 
, x and s are all varying! It turns out to be is easiest done by
switching variables from to s.
Label the distance from P
to the center of the sphere by r.
Then, from the diagram, 
, and a, r are constants, so 
,
and 
Now 
, and from the diagram 
, so 
,
and, writing 
,
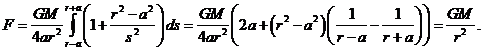
The derivation was rather lengthy, but the answer is simple:
The gravitational
field outside a uniform spherical shell is GM/r 2 towards the center.
And, there’s a bonus: for the ring, we only found the field along the axis, but for the spherical shell, once we’ve found it in one direction, the whole problem is solved—for the spherical shell, the field must be the same in all directions.
Field Outside a Solid Sphere
Once we know the gravitational field outside a shell of matter is the same as if all the mass were at a point at the center, it’s easy to find the field outside a solid sphere: that’s just a nesting set of shells, like spherical Russian dolls. Adding them up,
The gravitational
field outside a uniform sphere is GM/r
2 towards the center.
There’s an added bonus: since we found this result be adding uniform spherical shells, it is still true if the shells have different densities, provided the density of each shell is the same in all directions. The inner shells could be much denser than the outer ones—as in fact is the case for the Earth.
Field Inside a Spherical Shell
This turns out to be
surprisingly simple! We imagine the
shell to be very thin, with a mass density kg per square meter of surface. Begin by
drawing a two-way cone radiating out from the point P, so that it includes two small areas of the shell on opposite
sides: these two areas will exert gravitational attraction on a mass at P in opposite directions. It turns out that they exactly cancel.
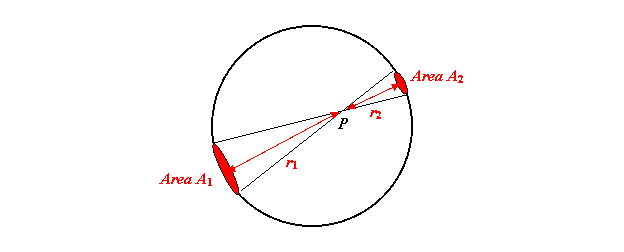
This is because the ratio of
the areas A1 and A2 at distances r1
and r2 are given by 
: since the cones have the same angle, if one cone has twice
the height of the other, its base will have twice the diameter, and therefore four times the area. Since the masses of the bits of the shell are
proportional to the areas, the ratio of the masses of the cone bases is also 
. But the
gravitational attraction at P from
these masses goes as 
, and that r2
term cancels the one in the areas, so
the two opposite areas have equal and opposite gravitational forces at P.
In fact, the gravitational
pull from every small part of the shell is balanced by a part on the opposite
side—you just have to construct a lot of cones going through P to see this. (There is one slightly tricky point—the line
from P to the sphere’s surface will
in general cut the surface at an angle.
However, it will cut the opposite bit of sphere at the same angle, because any line passing through a sphere hits
the two surfaces at the same angle, so the effects balance, and the base areas
of the two opposite small cones are still
in the ratio of the squares of the distances r1, r2.)
Field Inside a Sphere: How Does g Vary on Going Down a Mine?
This is a practical application of the results for shells. On going down a mine, if we imagine the Earth to be made up of shells, we will be inside a shell of thickness equal to the depth of the mine, so will feel no net gravity from that part of the Earth. However, we will be closer to the remaining shells, so the force from them will be intensified.
Suppose we descend from the Earth’s radius rE to a point distance r from the center of the Earth. What fraction of the Earth’s mass
is still attracting us towards the center? Let’s make life simple for now and
assume the Earth’s density is uniform,
call it kg per cubic meter.
Then the fraction of the
Earth’s mass that is still attracting us (because it’s closer to the center
than we are—inside the red sphere in the diagram) is 
.
The gravitational attraction
from this mass at the bottom of the mine, distance r from the center of the Earth, is proportional to mass/r2. We have just seen that the mass is itself proportional
to r3, so the actual
gravitational force felt must be proportional to 
.
That is to say, the gravitational
force on going down inside the Earth is linearly
proportional to distance from the center.
Since we already know that the gravitational force on a mass m at the Earth’s surface 
is mg,
it follows immediately that in the mine the gravitational force must be
.
So there’s no force at all at
the center of the Earth—as we would expect, the masses are attracting equally
in all directions.
Gravitational Potential Energy
Gravitational Potential Energy Near the Earth
We first briefly review the familiar subject of
gravitational potential energy near the Earth’s surface, such as in a
room. The gravitational force is of
course 
vertically downwards.
To raise a mass m, we must apply an upward force 
, balancing gravity, so the net force on the body is zero and
it can move upwards at a steady speed (ignoring air resistance, of course, and
assuming we gave it a tiny extra push to get it going).
Applying the steady force as the mass moves a small distance 
takes work 
, and to raise the mass m through a height h
takes work mgh. This
energy is stored and then, when the object falls, released as kinetic
energy. For this reason it is called potential
energy, being “potential kinetic energy”, and written
Note one obvious ambiguity in the definition of potential energy: do we measure h from the floor, from the top of our workbench, or what? That depends on how far we will allow the raised object to fall and convert its potential energy to kinetic energy—but the main point is it doesn’t matter where the zero is set, the quantity of physical interest is always a difference of potential energies between two heights—that’s how much kinetic energy is released when it falls from one height to the other. (Perhaps we should mention that some of this potential energy may go to another form of energy when the object falls—if there is substantial air resistance, for example, some could end up eventually as heat. We shall ignore that possibility for now.)
Onward and Upward
Let’s now consider the work involved in lifting something so high that the Earth’s gravitational pull becomes noticeably weaker.
It will still be true that lifting through 
takes work , but now 
, downwards. So
and to find the total work needed to lift a mass m from the Earth’s surface (rE from the center of the Earth) to a point distance r from the center we need to do an integral:
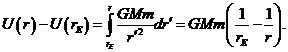
First check that this makes sense close to the Earth’s surface, that is, in a room. For this case,
Therefore
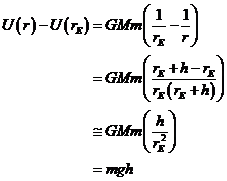
where the only approximation is to replace rE + h by rE in the denominator, giving an error of order h/rE, parts per million for an ordinary room.
To see what this potential function looks like on a larger scale, going far from the Earth, it is necessary first to decide where it is most natural to set it equal to zero. The standard convention is to set the potential energy equal to zero at r = infinity! The reason is that if two bodies are very far from each other, they have no influence on each other’s movements, so it is pointless to include a term in their total energy which depends on their mutual interaction.
Taking the potential energy zero at infinity gives the simple form
we plot it below with r in units of Earth radii. The energy units are GMm/rE, the -1 at the far left being at the Earth’s surface (r = 1), and the first steep almost linear part corresponds to mgh.
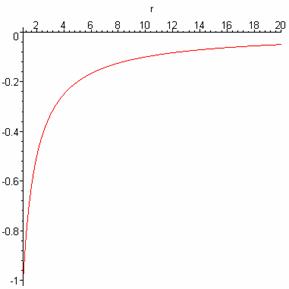
The above is a map of the potential energy “hill” to be climbed in going away from the Earth vertically upwards from any point. To gain a more three-dimensional perspective, the Earth can be visualized as being at the bottom of a “potential well” with flared sides, like this:
Or, from a different perspective:
A satellite in a circular orbit around the Earth can be imagined as a frictionless particle sliding around inside this “cone” at a fixed height, for an elliptic orbit the particle would slide between different heights.
Gravitational Potential
The gravitational
potential is defined as the gravitational potential energy per unit mass, and is often written 
. We shall rarely use it—the problems we
encounter involve the potential energy of a given mass m. (But is a valuable concept
in more advanced treatments. It is
analogous to the electrostatic potential, and away from masses obeys the same
partial differential equation, 
.)
Escape!
How fast must a rocket be moving as it escapes the atmosphere for it to escape entirely from the Earth’s gravitational field? This is the famous escape velocity, and, neglecting the depth of the atmosphere, it clearly needs sufficient initial kinetic energy to climb all the way up the hill,
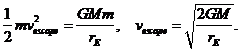
This works out to be about 11.2 km per sec. For the Moon, escape velocity is only 2.3 km per second, and this is the reason the Moon has no atmosphere: if it had one initially, the Sun’s heat would have been sufficient to give the molecules enough thermal kinetic energy to escape. In an atmosphere in thermal equilibrium, all the molecules have on average the same kinetic energy. This means lighter molecules on average move faster. On Earth, any hydrogen or helium in the atmosphere would eventually escape for the same reason.
Exercise: Saturn’s moon Titan is the same size as our Moon, but Titan has a thick atmosphere. Why?
Exercise: Imagine a tunnel bored straight through
the Earth emerging at the opposite side of the globe. The gravitational force in the tunnel is , as derived above.
(a) Find an expression for
the gravitational potential energy in the tunnel. Take it to be zero at the center of the
Earth.
(b) Now sketch a graph of the potential energy as a function of distance from the Earth’s center, beginning at the center but continuing beyond the Earth’s radius to a point far away. This curve must be continuous. Conventionally, the potential energy is defined by requiring it to be zero at infinity. How would you adjust your answer to give this result?
Potential and Kinetic Energy in a Circular Orbit
The equation of motion for a satellite in a circular orbit is
It follows immediately that the kinetic energy
,
that is, the Kinetic Energy = -1/2 (Potential Energy) so the total energy in a circular orbit is half the potential energy.
The satellite’s motion can be visualized as circling around trapped in the circular potential “well” pictured above. How fast does move? It is easy to check that for this circular orbit
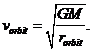
Recalling that the escape
velocity from this orbit is 
, we have
relating speed in a circular planetary orbit to the speed necessary, starting at that orbit, to escape completely from the sun’s gravitational field.
This result isn’t surprising: increasing the speed by Ö2 doubles the kinetic energy, which would then exactly equal the potential energy: that means just enough kinetic energy for the satellite to climb the hill completely out of the “well”.
Bottom line: the total energy of a planet of mass m in a circular orbit of radius r about a Sun of mass M is
Elliptic Orbits: Relevant Facts
From a practical point of view, elliptical orbits are a lot more important than circular orbits. A spaceship leaving earth and going in a circular orbit won’t get very far. And although proving the planetary orbits are elliptical is quite a tricky exercise, once that is established a lot can be deduced without further fancy mathematics.
Think about an astronaut planning a voyage from earth to Mars. The two important questions (apart from can I get back?) are:
How much fuel will this trip need?
How much time will it take?
It is crucial to minimize the fuel requirement, because lifting fuel into orbit is extremely expensive.
Ignoring minor refinements like midcourse corrections, the spaceship’s trajectory to Mars will be along an elliptical path. We can calculate the amount of fuel required if we know the total energy of the ship in this elliptical path, and we can calculate the time needed if we know the orbital time in the elliptical path because, as will become apparent, following the most fuel-efficient path will take the ship exactly half way round the ellipse.
Remarkably, for a spaceship (or a planet) in an elliptical orbit, both the total energy and the orbital time depend only on the length of the major axis of the ellipse—as we shall soon show.
Visualizing the orbit of the spaceship going to Mars, and remembering it is an ellipse with the sun at one focus, the smallest ellipse we can manage has the point furthest from the sun at Mars, and the point nearest to the sun at earth.
(Exercise: Sketch the orbits of earth and Mars, and this elliptical trajectory.)
This then immediately gives us the major axis of this smallest ellipse, so we can figure out, from the results given below, how much fuel and time this will take.
Here are the two basic relevant facts about elliptical orbits:
1. The time to go around an elliptical orbit once depends only on the length a of the semimajor axis, not on the length of the minor axis:
.
2. The total energy of a planet in an elliptical orbit depends only on
the length a of the semimajor axis,
not on the length of the minor axis:
These results will get you a long way in understanding the orbits of planets, asteroids, spaceships and so on—and, given that the orbits are elliptical, they are fairly easy to prove.
They follow from the two conservation laws:
total energy stays constant
angular momentum stays constant
throughout the elliptical orbital motion.
We’ll derive the results for a planet, beginning with the conservation laws. In fact, it turns out that all we need to use is that the energy and angular momentum are the same at the two extreme points of the orbit:
Labeling the distance of closest approach r1, and the speed at that point v1, the furthest point r2, the speed there v2, we have
and
.
From the second equation,
Rearranging, and dropping the common factor m,
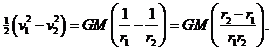
Using the angular momentum equation to write 
, and substituting
these values in this equation gives L2 in terms of r1,
r2:
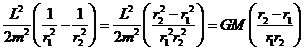
from which
The area of the ellipse is 
(recall it’s a circle
squashed by a factor b/a in one direction, so 
becomes ), and the rate of sweeping out of area is L/2m,
so the time T for a complete
orbit is given by:
To make further progress in proving the orbital time T depends on a but not on b, we need to express r1, r2 in terms of a and b.
Recall that the sun is at a focus F1 of the elliptical path (see figure below), and (from the “string” definition of the ellipse) the distance from the sun to point B at the end of the minor axis is a. Pythagoras’ theorem applied to the triangle F1BC gives
and from the figure
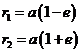
Therefore
Also from the figure
,
so we have the amusing result that the semimajor axis a is the arithmetic mean of r1, r2 and the semiminor axis b is their geometric mean.
Note from this that the angular momentum L has a simple form:
We’re now ready to find T:
So
,
a simple generalization of the result for circular orbits.
To prove that the total energy only depends on the length of the major axis, we simply add the total energies at the two extreme points:
The substitution in this equation gives
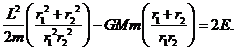
Exercise: substitute the expression for L2 in terms of r1, r2 to give E in terms of r1, r2. You will find
where a is the semimajor axis.
Exercise: From 
find the speed of the
planet at it goes through the point B
at the end of the minor axis. What is
its potential energy at that point?
Deduce that the total energy depends only on the length of the major
axis. (This is an alternative derivation.)
* Different Kinds of Orbits
Imagining the satellite as a particle sliding around in a frictionless well representing the potential energy as pictured above, one can see how both circular and elliptical orbits might occur.
(Optional: More formally, we solved the equation of motion in earlier notes to find
which is equivalent to the equation for an ellipse
as discussed there.)
However, that is not the whole story: what if a rogue planet comes flying towards the Solar System from outer space? What kind of orbit will it follow as it encounters the Sun’s gravity? In fact, our analysis of the equations of motion is equally valid in this case, and the (r,q ) equation is the same as that above! The new wrinkle is that e, which is always less than one for an ellipse, becomes greater than one, and this means that for some angles r can be infinite (the right-hand side of the above equation can be zero). The orbit is a hyperbola: the rogue comes in almost along a straight line at large distances, the Sun’s gravity causes it to deviate, it swings around the Sun, then recedes tending to another straight line path as it leaves the System.
Binary Stars
Up to this point, we’ve been considering gravitational attraction between pairs of objects where one of them was much heavier than the other, and was taken to be fixed. That is an excellent approximation for the Sun and the planets, or the planets and their satellites, but is not perfect. To see where it really breaks down, consider a binary star system with two equally massive stars. (Binary star systems are quite common.) In the simplest case, the two stars will orbit each other in circles, or, rather, by symmetry they will orbit a common central point:
For this case, the equation F = Ma must clearly be adjusted from the standard form above to:
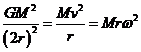
Problems with more than one rotating body turn out to handle
more easily if the acceleration is written 
, as will soon be evident.
Consider now a binary system in which one star has mass M, the other 2M, but stay with the simple case of circular orbits. This time both stars go in circles around the
common center of mass, and of course both move at the same angular velocity w, so their angular accelerations are 
respectively, the accelerations are in inverse proportion to
the masses, as the must be since both experience the same magnitude force, their
mutual gravitational attraction.
*The Earth-Moon System: Tidal Forces
The Earth’s mass is about eighty times the Moon’s mass. This means that the Earth and the Moon both circle the system center of mass, a point about one-eightieth of the way from the center of the Earth to the center of the Moon—about 3,000 miles from Earth’s center, so still inside the Earth.
To compute the Moon’s orbital period, if we need to be precise, we should adjust the equation previously used to
where r is the
Earth-Moon distance, and 
is the Moon’s distance
from the system center of mass. Putting 
gives close to 1% accuracy, usually adequate for our purposes
here, but clearly not for precision astronomy.
Another important point is that to find the gravitational force on the Moon, we take it to be the same as if all the Moon’s mass were concentrated at a point in the center. Assuming the Moon is spherically symmetrical, this is ok. We’ve established that the force on a mass outside the Moon is the same as if all the Moon’s mass were at the center, so, since the gravitational forces are equal and opposite, the force on the Moon from the mass is the same as if all the Moon’s mass were at the center. Therefore, the gravitational force of the Earth on the Moon, which can be thought of as the sum of all the one kilogram masses making up the Earth, must be the same as if all the Moon’s mass were at the center.
To see the effect of the variation of the Earth’s
gravitational field on objects at the Moon’s surface, imagine the four small
red squares in the diagram to be rocks at different points on the Moon’s
surface. The Moon’s large circular path
around the Earth is indicated by the broad gray line above and below the
circle. For rock A on the orbital line, that is, at the same distance from Earth as
the center of the Moon the Earth’s gravitational pull (blue arrow) exactly
accounts for the rock’s acceleration towards Earth 
from the orbital
circular motion.
Now consider rock B
on the left, closer to earth. It will
feel a stronger gravitational pull
from the Earth, than rock A does, yet
its acceleration is less than rock A’s acceleration. What about 
? The answer is that
we’ve been neglecting the other forces on the rock: the Moon’s own
gravitational pull downwards (meaning, of course, towards the center of the
Moon) and the “normal” reaction of the Moon’s surface that the rock is resting
on. These forces didn’t matter for rock A, because they were at right angles to
the Earth’s pull and the acceleration, and they canceled each other. But for rock B they cannot cancel, we need them to get ! Since the rock’s
acceleration is less (see diagram) than that which would be given by the
Earth’s gravity alone, the Moon’s gravitational pull (which acts to the right
for rock B) must be greater than the normal force from the
surface. So, if the rock were resting on a spring scale, the scale would
register a smaller weight than it would for the identical rock at A.
That is to say, rock B is
resting more lightly on the surface than rock A is.
Let’s now look at rock C. Being further from the Earth, but going
around with the Moon at the same angular velocity w, its acceleration is greater than rock A’s, but the Earth’s gravitational pull is weaker at the greater distance.
Again, to satisfy , the Moon’s gravitational pull on the rock at C, plus the normal force from the
surface, must not balance. In fact, the net
force from these two must point left (towards the Earth) to give the greater
acceleration. Therefore, the Moon’s
gravitational pull must be stronger than the normal force from the
surface. That means that a rock at C placed on a spring scale will register
a smaller weight—the same effect as
at B!
This means that rocks at B and C will experience what amounts to an apparently lower gravitational pull to the Moon’s center than a rock at A. Imagine now that the Moon were covered with an ocean. The effectively stronger gravity at places like A would pull the water down more than the weaker effective gravity at B, C. This is the origin of tides: the high tide is where “gravity” is weakest, on two opposite sides. Of course, there is no ocean on the Moon, but this same argument works for the effect of the Moon’s gravity on the Earth: remember the Earth is also circling the Earth-Moon system center of mass.