Oscillator Homework Problems
Michael Fowler 3/20/07
1. Dimensional exercises: use dimensions to find a characteristic time for an undamped simple harmonic oscillator, and a pendulum. Why does the dimensional argument work for any initial displacement of the oscillator, but only small swings of the pendulum?
What possible characteristic times can be found dimensionally for a damped oscillator? Explain the physical significance of these times for a heavily damped oscillator, and a lightly damped oscillator.
2. Open the damped oscillator spreadsheet. Let’s first examine damped motion without the spring. Set m = 1, k = 0, b = 3, xinit = 0, vinit = 3.
(a) How does the curve relate to the dimensionally derived time(s) for a damped oscillator?
(b) Write down the equation for this damped k = 0 “oscillator”. (Of course, this won’t oscillate!).
Put dx/dt = v, to get a first-order equation for v. Solve it, and see if your solution agrees with the spreadsheet curve.
(c) Now you’ve found v(t), you know dx/dt. Write down and solve the equation for x(t), and check that it agrees with the spreadsheet.
(d) Bring back the spring: set k = 1. Does this significantly change the initial shooting upwards of the curve? What, then, are the important terms in the equation for that part of the motion?
(e) Look at the very top of the curve, the maximum value of x: what are the important terms in the equation in that neighborhood?
(f) For longer times, which terms in the equation dominate. Drop the least important term, and solve the remaining equation. Then check to see if this is a good approximation or not.
3. Open the damped oscillator spreadsheet. Fix the constants to give the critical damping curve. Then lower the damping b until you can detect the oscillator going past the origin.
(a) Roughly, by what percentage do you need to lower b to see this?
(b) Suppose in building a model for a shock absorber you were willing to let the downward swing be as much as 5% of the original upward displacement, and you take m = 1, k = 1 for the model, what would be the value of b?
4. Open the damped driven oscillator spreadsheet and put k = 1, b = 0.1, omega = 1.25, delta_t = 0.055.
(a) What’s going on at the beginning? It might help to set b = 0 temporarily to get some insight.
(b) Note that the solution settles down to a steady state. Does the time to settle down depend on the initial conditions? Change them and find out. Set xinit large, for example. Can you arrange the initial conditions so that the steady solution takes over immediately? How would you do that?
5. (a) Open the pendulum spreadsheet. See how the period varies with the amplitude: it’s initially set at 0.1 radian. Try 1 radian, 2 radians, 3 radians.
(b) In the pendulum spreadsheet, set the initial angle theta_init =0, then try the initial angular velocity omega_init = 4, 5, 6, 7. Interpret your result. How can you make the pendulum period very long?
6. An unpowered streetcar is accelerating under gravity down a ten degree slope. Neglect friction and air resistance, assume the acceleration is the same as a smooth block sliding down a frictionless surface. A pendulum of length l is hung from the ceiling inside.
(a) If the pendulum is at rest, what is the direction of the string?
(b) What is the period of oscillation of the pendulum?
7. Some future civilization bores a tunnel vertically down, through the center of the earth, emerging at the opposite point on the globe. The air is pumped out of the tunnel, leaving a vacuum. Passenger pods are dropped into the tunnel. Assume any friction to be negligible.
(a) How long does a one-way trip to the other end of the tunnel take?
(b) How does that compare with a satellite in low orbit getting from one end to the other?
(c) Another straight-line tunnel is bored from
8. A 1 kg mass rests on a spring. A gentle downward pulse causes vertical
oscillations at 5Hz.
(a) Suppose a balloon is attached to the top of the mass. The balloon has a mass of 0.05kg, but feels a buoyancy force able to lift 0.55 kg. How does this affect the period of the oscillation?
(b) What would be the period of the mass + spring (no balloon) on the Moon? (gMoon = 2 m/s2.)
9. A spring is hanging vertically at rest. A mass held in the hand is gently attached to
the end of the spring, then released.
The system oscillates, the maximum downward distance being 3 cm below
the original position.
What is the period of oscillation?
10. Let us represent a ship weighing 20,000 tons (1 ton = 1,000 kg) by a rectangular parallelepiped, 150 m long, 30 m across, 20 m deep. Show that in vertical motion, this ship behaves as a simple harmonic oscillator, and find the period.
11. A flat horizontal plate driven from below oscillates vertically with an amplitude of 1 mm. Some sand (of negligible mass) is sprinkled on the plate. The frequency of the oscillator is gradually increased from zero. At what frequency will the sand lose contact with the plate? At what point in the cycle will this happen?
12. (a) Prove that
for a lightly damped oscillator, the change in frequency caused by the damping
is approximately 
(b) If damping causes a 1% decrease in the frequency of an oscillator, what is its Q value? Over how many cycles does the energy drop by 1/e? Over how many cycles does the energy drop by ½?
13. A lightly damped oscillator has mass m, spring constant k and damping factor b.
(a) Prove that at any instant of time the rate of loss of energy is bv2 joules/sec., v being the instantaneous velocity.
(b) Assuming the change in amplitude in a single cycle is negligible, what is the average value of v2 over the cycle compared with the maximum value of v2 ?
(c) If he energy loss in one second is small, show that it
is well approximated by 
, and deduce that for long times the energy decays as 
14. A lightly damped driven oscillator exhibits a strong
resonance at frequency 
Prove that at
resonance, the total energy in the oscillator for a given driving force is
proportional to Q2.
15. An old but
precisely made pendulum clock keeps time within one second a day in
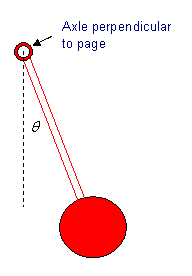16.
The bob of a pendulum is a uniform disk of radius 4 cm , attached to the end of
a very light rod, so that the center of
the bob is a distance 30 cm from the
support axle (which would be perpendicular to the page).
(a) Find the moment of inertia of the bob about the axle (you’ll need to use the Parallel Axis Theorem).
(b) For small oscillations, what percentage error arises in using the simple point-mass approximation?
17. We proved in the lecture that the steady-state solution for the damped oscillator driven by a force
is
(a) Prove that the total energy in the oscillator, kinetic + potential, usually varies through the cycle. Explain why, by comparing the rate of working of the driving force and that of the damping force. Show that the variation disappears at resonance.
(b) Prove that at the resonant frequency, the energy in the oscillator is
(c) Prove that the power input (rate of working) of the driver at resonance is
(d) The power input will drop to half on varying 
away from resonance when
the denominator
doubles. Assume Q
is large, so you can replace 
by 
over this range, and conclude the power input is halved at 
Sketch very roughly
the power input as a function of driving frequency for a large Q, then for double that Q on the same
sketch.