To start : make sure you are comfortable with the contents of Appendices A, B, C, (D), E .

Appendix A

Scientific Notation: how to deal with very large and very small numbers.

Rather than writing, e.g., 3,570,000,000 or 0.000000043, it is much more convenient to write 3.57 x 10⁹ or 4.3 x 10^-8

(remember : 0.1 = 1/10 = 10^-1, 0.01 = 1/100 = 10^-2, etc. Also remember: 10⁰ =1)


Multiplication and division rules :

$(a\times 10^{n}) \times (b\times 10^{m}) = a\times b\times 10^{n+m}$

$a\times 10^{n}/b\times 10^{m} = a/b\times 10^{n-m}$

Examples : .....






But do not forget how to do additions .....

Appendix B

Significant figures : in Physics, as in all other sciences, quantities are known with limited precision. This is expressed in terms of significant figures.

For example, suppose that the height of a person is 1.8 meters (about 6 ft) Question : with what precision is this height known?

If I try to judge the height from a distance, probably my precision would be no better than 10 cm or so. I would express that by saying that my estimate is 1.8 m, meaning that the height is probably more than 1.7 m but less than 1.9.

A more accurate measurement will probably give me a precision of the order of centimeters, so I can say that the height is 1.80 meters. Although mathematically 1.8 and 1.80 are the same number, in science they are interpreted differently : they represent quantities that are known respectively with a precision of either 2 or 3 significant figures.
When operating with quantities of a given number of significant figures, the result can only be as accurate as the least accurate of the operands.

Appendix E

Trigonometry : I expect that 99% of the trigonometry we will need will be limited to the standard expressions for right triangles :

$$\sin\theta = b/c \sin\phi = a/c$$

$$\cos\theta = a/c \cos\phi = b/c$$

$$\tan\theta = b/a \tan\phi = a/b$$

$\sin\theta = \cos\phi ; \sin\phi = \cos\theta$

(this is because we are dealing with a right triangle, therefore 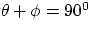$\theta + \phi = 90^{0}$, and remember that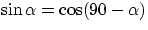 $\sin\alpha = \cos (90-\alpha)$

In general : all the angles and sides of a right triangle can be fully determined if you know

1.

either two sides , or

2.

one side and one angle

Chapter 1

Units

When reporting the value of any physical quantity, the number by itself is not meaningful unless we also specify the UNITS of the measured quantity.

Units can be (and have been) chosen arbitrarily, in a way as to be suitable with the problem at hand. Because of the arbitrary choice, historical and geographical factors have led to the existence of several different units to measure the same quantities, and this of course can lead to confusion.

Following an almost universal (as of today) scientific agreement, we will use, for the base (or fundamental) quantities of LENGTH, MASS and TIME the respective units of METER, KILOGRAM and SECOND, and their decimal multiples and submultiples.

But of course, whenever convenient, we can use any other unit we like, therefore we must know how to convert between different units. Handy rule : treat units, and their conversion factors, as algebraic quantities.

Examples :

1.

inches into cm

2.

square feet into liters. Can I do that ?.......


of course not, but I can do cubic feet into liters

3.

snail hours into light years. Can I do that ? .....


light year : distance covered when moving at the speed of light for one year
snail hour : distance covered when moving at a snail's pace for one hour

Both units measure a distance, therefore it is legitimate to convert one into the other

Important lesson : I can only convert between units that represent quantity of the same dimension. Similarly I can only add quantities when they have the same dimension (and, to do the addition, it is better if I convert them to the same units). Specifically :

it makes sense to add, e.g. , cm to inches, and, to get a meaningful result , it would be advisable to convert them to the same unit (either cm or in). But it doesn't make sense to add, e.g., cm to seconds. On the other side, it is perfectly legal to multiply or divide quantities of different dimensions and, when we do so, we create a new physical quantity, with its own dimension. Most obvious example (we will meet many more in the future) :

LENGTH / TIME = VELOCITY, whose units will always be a length/time, e.g. miles/hour, meters/second, etc. etc.

[Velocity] = [L/T] = [LT^-1]

In any equation containing physical quantities, the dimensions on the right hand side have to be the same as those on the left hand side.

Scalars and Vectors

In many instances, a quantity is fully specified by a number (and the appropriate unit). When I say that the temperature of a room is 65 degrees, or that the mass of an object is 3.5 kg, this is all that I need to know. In other cases, giving a number is not enough : if I say that I have moved over a distance of 2 km, or that I am moving with a velocity of 35 miles/hour, this does not provide full information, since it does not tell me in which direction I am moving or have moved.

A quantity that, to be fully specified, needs both a magnitude and a direction is called a VECTOR. Quantities fully specified by just a number are called SCALARS.



By convention, a vector is drawn with a length proportional (in arbitrary units) to its magnitude. In text, vectors are usually indicated with bold characters or with an arrow above the symbol.

Vector Addition
(graphic procedure)

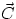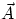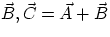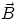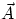The rule for adding vectors is very simple : if I want to find the sum $\vec{C}$ of the vectors $\vec{A}$ and $\vec{B}, \vec{C} = \vec{A} + \vec{B}$, all I need to do is to draw $\vec{B}$ with its tail touching the head of $\vec{A}$, and join the tail of 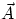$\vec{A}$ with the head of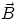 $\vec{B}$


This procedure would also allow me to add many vectors in a single step.

Vector subtraction is equally simple, if I remember that

$\vec{A} - \vec{B} = \vec{A} + (-\vec{B})$,

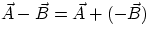
and that to change the sign of a vector I just need to change its direction.

Vector Components

The graphic procedure for vector operations is neat, but it might not always be practical to perform. We need a way of operating upon vectors in a purely mathematical way. This can be done by introducing the components of a vector. The components of a vector are defined with respect to a given frame of reference, i.e a set of x,y,(z) axes (in spite of the fact that we live in a three-dimensional world, throughout this course we will almost exclusively deal with two dimensions only). Vector components : perpendicular projections of the vector onto the two axes


From what we have learnt about vector sum, we see immediately that

$\vec{V} = \vec{V_{x}} + \vec{V_{y}}$

Important : notice that the components of a vector are not absolute quantities but depend upon the choice of axes. A different choice will give different components for the same vector. This also means that, for any specific problem, one is allowed to make the most suitable choice of axes.

If a vector makes an angle 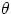$\theta$ with the x-axis, one has immediately :

$V_{x} = V\cos\theta\hspace{1.in}V_{y} = V\sin\theta$,

and also

$V = \sqrt{V_{x}^{2} + V_{y}^{2}}\hspace{1.in}\tan\theta = V_{y}/V_{x}$

Vector Addition
numerical procedure

If 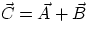$\vec{C} =\vec{A} + \vec{B}$, then one has :

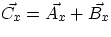
$\vec{C_{x}} =\vec{A_{x}} + \vec{B_{x}}$, and $\vec{C_{y}} = \vec{A_{y}} + \vec{B_{y}}$,

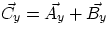
i.e. the components of the sum are given by the sum of the components. Given that a vector is completely defined by its components, the expressions above tell us how to add two vectors "numerically" rather than "graphically" :

1.

find the components of the terms to be added, A_x, A_y, B_x, B_y (pay attention to the sign)

2.

add separately the x and y components to find the components of the sum-vector

3.

when the components are known, magnitude and angle of the sum vector are readily found : $V = \sqrt{V_{x}^{2} + V_{y}^{2}},\tan\theta = V_{y}/V_{x}$

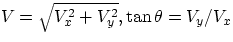
Conceptual Questions 12, 13, 14, 18, 20