


Next: About this document ...
Lecture 10
Impulse, Momentum and Collisions
We are going to take another look at Newton's second law, the way that Newton himself actually
looked at it. So far, we have written 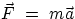 , but remembering that
, but remembering that 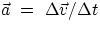 , we can write
The quantity
, we can write
The quantity 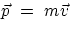 is called the momentum and it plays a very
important role in the study of mechanics. In terms of momenta, we can then write :
Notice that this expression, which is in fact the way thatNewton had written his law, is more
general than the one we have used so far, since it also allows, in a given problem, for the mass
to change. A problem of motion involving mass changes is not too much out of the ordinary,
standard examples are a wagon full of sand with a hole at the bottom, or a space rocket that
consumes considerable amount of fuel (i.e. of its initial mass) as it goes along, etc.
When dealing with sub-atomic particles (my favourite "hobby" when I am not teaching pre-meds)
mass can easily change into energy and viceversa, and, to handle that, it is better to deal
with momenta rather than velocities.
is called the momentum and it plays a very
important role in the study of mechanics. In terms of momenta, we can then write :
Notice that this expression, which is in fact the way thatNewton had written his law, is more
general than the one we have used so far, since it also allows, in a given problem, for the mass
to change. A problem of motion involving mass changes is not too much out of the ordinary,
standard examples are a wagon full of sand with a hole at the bottom, or a space rocket that
consumes considerable amount of fuel (i.e. of its initial mass) as it goes along, etc.
When dealing with sub-atomic particles (my favourite "hobby" when I am not teaching pre-meds)
mass can easily change into energy and viceversa, and, to handle that, it is better to deal
with momenta rather than velocities.
The expression we have just found, relating variations of momenta to the quantity 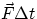 , the impulse, is extremely useful, since it allows to study phenomena that occur
over very short times. Example : what is the use of air bags? We are not going to smash a car
against a wall, we will instead throw an egg....
, the impulse, is extremely useful, since it allows to study phenomena that occur
over very short times. Example : what is the use of air bags? We are not going to smash a car
against a wall, we will instead throw an egg....
The lesson we learn is that, in a car crash, the car, and its occupants, rapidly change their
momenta from mv to 0. To minimize the effect of the impact, we want to decrease the average
force acting on the car occupants. The relation we have found tells us that, for a given change
of momentum the quantity  has a well defined value: we can therefore make F
as small as possible by making
has a well defined value: we can therefore make F
as small as possible by making 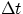 (i.e. the time over which the change of momentum
takes place) as large as possible.
(i.e. the time over which the change of momentum
takes place) as large as possible.
Conservation of (Linear) Momentum
From the expression
we can see that if no net force is acting on a "system", its total momentum remains constant.
So far we have mostly studied the motion of individual objects but this result allows us to
investigate more complex situations, where several objects interacting with each other are
involved. If we have a "system" comprising several bodies, we should distinguish between
internal and external forces :
- 1.
- we call internal, the forces acting between members of the system, while
- 2.
- we call external the forces due to some agent which is not part of the system
If we consider the case of a system where no external forces are present (i.e. the only forces
present are internal, this is also called an isolated system), we see that the
totality of all internal forces must add up to zero. This is an immediate consequence of
Newton's third law : for every force that a given member of the system A exerts on a member B,
B will respond with an equal and opposite force, and this is true for every (internal) force
present. We can than conclude that, for an isolated system, all the forces add up to zero,
therefore 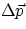 = 0, i.e.
= 0, i.e.
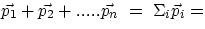
constant
where the symbol 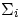 represents the sum of all the individual momenta of the members
of the system. We should stress right away that this expression represents a sum among vectors (
momenta are vector quantities), and it implies that the sum of the components must be separately
equal to some constant
represents the sum of all the individual momenta of the members
of the system. We should stress right away that this expression represents a sum among vectors (
momenta are vector quantities), and it implies that the sum of the components must be separately
equal to some constant
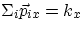
and
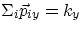
, with
kx,
ky= constants
Examples :
- 1.
- measure the velocity of a speeding bullet
- 2.
- a bomb (at rest) explodes into three pieces (problem 7.57)
- 3.
- a moving projectile breaks up into two pieces (problem 7.59)
Remark : when deciding whether momentum is conserved or not, make sure you are clear on what
is your "system", and what are the external and internal forces. On page 197, the book gives
the example of a system consisting of two billiard balls either when they collide (no external
force, momentum is conserved) or when they fall to the ground (momentum is not conserved). Can
you think of broadening this last picture, so as to have again a case of momentum conservation?
Momentum conservation is routinely exploited to analyze collisions. For these cases, in addition
to momentum conservation we can, under certain circumstances, also apply Kinetic Energy
Conservation.
When dealing with collisions, we distinguish 3 cases:
- 1.
- Elastic Collision : we define an elastic collision one in which both momentum and kinetic
energy are conserved. The colliding objects bounce off each other elastically. Simplest case :
a moving ball hits an identical stationary ball with a perfect head-on collision....
Momentum conservation is not sufficient to tell us the motion after collision, but if we
include energy conservation the solution is unique (as any billiard player will know)
- 2.
- Inelastic Collisions : in this case, typical e.g. of car crashes, momentum is conserved,
but total kinetic energy is not, since part of the input energy causes permanent deformations
plus heating by friction. To solve these problems, we need to have some information on the
amount of lost energy.
- 3.
- Totally Inelastic Collision : this is the extreme case, where the colliding objects
stick together after collision (it could be shown that this case represents the maximum possible
energy loss compatible with momentum conservation). To solve these problems, we are helped by
the fact that, in the final state, there is only one unknown velocity (simplest example : as
in 1., but someone had stuck a piece of chewing-gum on the stationary ball....here momentum
conservation is enough to solve the problem. How much kinetic energy is lost?)



Next: About this document ...
Sergio Conetti
10/11/1999
![]() , the impulse, is extremely useful, since it allows to study phenomena that occur
over very short times. Example : what is the use of air bags? We are not going to smash a car
against a wall, we will instead throw an egg....
, the impulse, is extremely useful, since it allows to study phenomena that occur
over very short times. Example : what is the use of air bags? We are not going to smash a car
against a wall, we will instead throw an egg.... ![]() has a well defined value: we can therefore make F
as small as possible by making
has a well defined value: we can therefore make F
as small as possible by making ![]() (i.e. the time over which the change of momentum
takes place) as large as possible.
(i.e. the time over which the change of momentum
takes place) as large as possible.