


Next: About this document ...
Lecture 13
Newton's Law for Rotational Dynamics
We are now ready to make the last step, i.e. to examine the dynamics of rotational
motions for the non-equilibrium case. And to do that, we will find out how Netwton's
"F=ma" law looks like when expressed in term of angular quantities [it is useful to
remind ourselves why we want to use angular variables when dealing with rotations:
the reason is that, for a rotating body, angular quantities like angular
velocity and accelerations are the same for each point of the body, while the linear
(or tangential) quantities do vary according to the radius; this will also mean that
quantities that depend upon the linear velocity, like kinetic energy and momentum, are
not easily defined for a rotating rigid body, unless we succeed in expressing them in
terms of angular variables].
So let us consider a body free to rotate around an axis, and let us apply to it
a force F perpendicular to the axis and at a certain distance from it (so that the
lever arm is not zero). For an arbitrary very small volume of mass mi and located
at a distance ri from the rotation axis we can write
Fi=
miai
Firi =
miairi
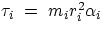
where we have remembered the definitions of torque and of angular acceleration.
This represents the effect of the elementary torque felt by an (arbitrarily small) section
of our rotating object. To find the expression for the whole body, we would have to sum
all the individual elementary contributions, i.e.
with  and taking advantage of the fact that
and taking advantage of the fact that 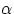 is the
same for all the elements of the rotating body, therefore it can be factored out of the
sum.
is the
same for all the elements of the rotating body, therefore it can be factored out of the
sum.
The expression 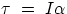 is exactly what we were looking for, as it relates
torques to angular accelerations.The expression is in fact nothing but F=ma, but
written in a more convenient form. The quantity
is exactly what we were looking for, as it relates
torques to angular accelerations.The expression is in fact nothing but F=ma, but
written in a more convenient form. The quantity 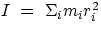 is
called moment of inertia, and it plays for rotations a role analogous to that
of the mass for translations, since it represents a measure of the resistance (i.e. of the
inertia) that a body opposes to undergo angular acceleration when subjected to a
torque. But note that the moment of inertia I is not an intrinsic attribute of a given
body, since it is defined with respect to a given axis of rotation. For different
choices of axis, the same body will have different values of I.
is
called moment of inertia, and it plays for rotations a role analogous to that
of the mass for translations, since it represents a measure of the resistance (i.e. of the
inertia) that a body opposes to undergo angular acceleration when subjected to a
torque. But note that the moment of inertia I is not an intrinsic attribute of a given
body, since it is defined with respect to a given axis of rotation. For different
choices of axis, the same body will have different values of I.
Techniques of Integral Calculus allow to compute the Moment of Inertia for bodies of
regular shape (see Table 9.1). For a body of irregular shape, it can be determined
by measurement.
How ?? Obviously by applying to the body a known torque, and measuring
its (angular) acceleration (see e.g. Problem 9.29).
Rotational Energy
We have learnt how a body moving with velocity v has a kinetic energy given by
E=1/2mv2. And we have also seen that to give an object initially at rest a certain
amount of kinetic energy, one has to perform an equivalent amount of work, the work being
given by the product F x s. If we now consider a rotating body, it is obvious that it
possesses kinetic energy (every point of the body is moving with some velocity), and that
work is required to transfer that amount of energy to it. You could probably guess what
will be the epressions for rotational work and energy, when described in terms of angular
quantities:
an object rotating with angular velocity  has a rotational kinetic energy
given by
where I is the body's moment of inertia; and this energy could be gained by doing an amount
of work given by
What about the sign of W ? Probably the best way to determine the sign of the work done
by a torque is to think that positive work will increase the kinetic energy of a body,
while negative work will decrease it (e.g. if friction brings a rotating flywheel to a
stop, friction has done negative work).
has a rotational kinetic energy
given by
where I is the body's moment of inertia; and this energy could be gained by doing an amount
of work given by
What about the sign of W ? Probably the best way to determine the sign of the work done
by a torque is to think that positive work will increase the kinetic energy of a body,
while negative work will decrease it (e.g. if friction brings a rotating flywheel to a
stop, friction has done negative work).
We can then conclude that a translating object has kinetic energy 1/2mv2, while for a
rotating one 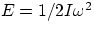 . But what if the object is both translating and rotating
(e.g. a spinning football, or a gymnast doing somersaults, or even the wheel of a
moving car)? Well, in this case the object will have both translational and
rotational kinetic energy, and if a certain amount of total work is done on the body,
this work in general will go to modify both quantities. Moreover, the principle of
mechanical energy conservation for a body subjected only to conservative forces will
have to include rotational energies. Specifically, for a body moving under the sole
influx of gravity, we will have
. But what if the object is both translating and rotating
(e.g. a spinning football, or a gymnast doing somersaults, or even the wheel of a
moving car)? Well, in this case the object will have both translational and
rotational kinetic energy, and if a certain amount of total work is done on the body,
this work in general will go to modify both quantities. Moreover, the principle of
mechanical energy conservation for a body subjected only to conservative forces will
have to include rotational energies. Specifically, for a body moving under the sole
influx of gravity, we will have
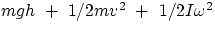
= constant
(A legitimate question : if a body has extended dimensions, what is the correct choice
for "h" ? Any guess ? )
The fact that rotational energy has to be included when dealing with falling (and
rolling) objects has some, maybe surprising, consequences, e.g.
- rolling bodies fall "more slowly" than sliding bodies. And, not surprisingly,
the rate of "rolling down" will depend upon the value of I, the moment of inertia.
- not all all parts of a rotating falling body fall at the same rate: according to
its relative location, a point can have acceleration larger or smaller than "g".
Angular Momentum
You can guess the next step : as a translating body has a linear momentum given by
p=mv, so a rotating body has an angular momentum given by L=I .
And, with arguments similar to the ones we applied to the linear case, we could also show
that, when a system is not affected by external forces, its total angular momentum
remains constant. Simple demonstrations can verify the validity of the principle of
conservation of angular momentum.
.
And, with arguments similar to the ones we applied to the linear case, we could also show
that, when a system is not affected by external forces, its total angular momentum
remains constant. Simple demonstrations can verify the validity of the principle of
conservation of angular momentum.
Conceptual Questions 9.20, 9.21



Next: About this document ...
Sergio Conetti
10/22/1999
![]() . But what if the object is both translating and rotating
(e.g. a spinning football, or a gymnast doing somersaults, or even the wheel of a
moving car)? Well, in this case the object will have both translational and
rotational kinetic energy, and if a certain amount of total work is done on the body,
this work in general will go to modify both quantities. Moreover, the principle of
mechanical energy conservation for a body subjected only to conservative forces will
have to include rotational energies. Specifically, for a body moving under the sole
influx of gravity, we will have
. But what if the object is both translating and rotating
(e.g. a spinning football, or a gymnast doing somersaults, or even the wheel of a
moving car)? Well, in this case the object will have both translational and
rotational kinetic energy, and if a certain amount of total work is done on the body,
this work in general will go to modify both quantities. Moreover, the principle of
mechanical energy conservation for a body subjected only to conservative forces will
have to include rotational energies. Specifically, for a body moving under the sole
influx of gravity, we will have