


Next: About this document ...
Lecture 14
Elasticity
Whenever a force is applied to an object which is constrained not to move, the effect of
the force will be to cause a deformation. This effect is in general not very visible,
since the deformations are very small, especially if the object is very rigid,
i.e. not very elastic (a perfectly rigid body is defined as one where the distance
between any two points does not change, elastic is exactly the opposite).
Given a body of somewhat regular shape, one can think of applying forces perpendicular to
one surface (stretching or compressing), parallel to it (shear) or somewhat
uniformly to the whole bulk of the body. In general, one says that a certain
stress causes a certain strain.
All of these situations are handled in a similar way, by realizing that the deformation in
the object under stress is, over a fairly wide range, proportional to the force applied.
More specifically, one describes the effects in terms of fractional (or percentage)
deformation, i.e., for e.g. the case of stretching:
where F is the applied force, L is the unstretched length of the body, A its cross section,
and Y (Young's modulus) is a constant, characterisitc of the material under exam.
Given that the deformation caused by ordinary forces are very small, the
values of Y (measured in N/m2) are very large (Y=1 would imply that the force of 1 N
stretches a sample of unit cross section (1 m2) by 100%, hardly an everyday occurrrence)
Obviously an expression like the one above cannot be valid for any
arbitrary value of applied force : when stretching an object with ever increasing force,
we will say that we are in the elastic regime if, after the force ceases, the objects regains
its original length. But even when in the elastic regime, the proportionality described by the
above formula will be valid only up to a certain point.
When the force exceeds the elastic limit, the body will undergo
permanent deformation (this is the "plastic regime", think of of putty or of pizza dough ....).
If we keep increasing the force, we will eventually reach the breaking point.
Similar considerations also apply to shear and bulk deformations, which are described by similar
expressions:

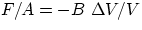
,
with S and B respectively the Shear and the Bulk moduli. Notice that the relevant quantity is not
just the force, but the force per unit surface, F/A. This quantity is referred to as either
stress or pressure, and is measured in pascal= newton/m2 (stress is
more commonly used for solids, pressure for liquids or gases.
Problem 10.14
Springs.
In many cases, we want to deal with objects that exhibit substantial (elastic) deformation
when subjected to even ordinary forces : this is e.g. the case of springs. When dealing
with springs, it is customary to think in terms of absolute rather than relative elongation.
In other words, if applying a force F causes the spring to lengthen (or shorten) by an amount
x, we write :
F=kx
where k is the spring constant. The bigger the value of the spring constant, the
stiffer is the spring. It is easy to see the relation between spring constant and
Young modulus. From
F=kx=YAx/L, we get k=AY/L
from which we can see, in a much more direct way than the one followed in example 5, that if we
cut a given spring into two pieces, the pieces are twice as stiff as the original spring.
When dealing with a stretched or compressed spring, we can think either in terms of the force
required to compress or stretch it by an amount x (F=kx) or of the force exerted by the
spring itself upon you (F=-kx, by Newton's third Law).
Knowing the force, we should be able to study the motion of a mass driven by a spring:
which tells us that the problem is not too simple, since the force depends on the position, but
the position changes all the time, and therefore so does the force (a rigorous solution requires
elementary calculus, see the Appendix).
But even if we do not know what the solution will look like, direct experience and thought can
give us a fairly good idea : if we attach a mass m to a spring, stretch it and let it go, the
spring will tend to return to its equilibrium value and, in doing so it will give some
acceleration to the mass. When the system reaches the spring's position of equilibrium, the mass
has a certain non-zero velocity (therefore some kinetic energy); due to inertia, the mass will
tend to continue its motion and compress the spring, until all of its energy is used and it comes
to rest. But now the spring will want to go back to its equlibrium position, in doing so it
will put the mass back in motion .... etc. etc. The resulting motion is that of a periodic
oscillation. The mathematical solution would confirm this result : the motion of a mass
attached to a spring is properly described by the cosine function:
where xmax is the amount by which the string was stretched before setting the mass in motion.
Why does the expression in parenthesis (the "argument" of the cosine) look the way we have written
it? Here is the reasoning :
at t=0 the mass is at x=xmax, this is in agreement with the formula above, since
 . We have seen the the motion is a periodical oscillation. If T is the period (i.e.
the time it takes to perform a full oscillation) then at time t=T the mass must be back at
xmax. And this is in fact what the equation says, since
. We have seen the the motion is a periodical oscillation. If T is the period (i.e.
the time it takes to perform a full oscillation) then at time t=T the mass must be back at
xmax. And this is in fact what the equation says, since 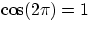 , in fact
, in fact 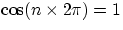 , the oscillation keeps repeating over and over.... A motion described by the
above expression is called simple harmonic motion.
, the oscillation keeps repeating over and over.... A motion described by the
above expression is called simple harmonic motion.
Circular vs. Harmonic Motion
Harmonic motion can be investigated more in detail by realizing that, if an object is moving
with uniform circular motion (i.e moving in a circle with constant angular velocity  ),
then its projection on an arbitrary axis will move with simple harmonic motion. Specifically,
if r is the circle's radius,
where we have remembered the relation between angular velocity
),
then its projection on an arbitrary axis will move with simple harmonic motion. Specifically,
if r is the circle's radius,
where we have remembered the relation between angular velocity  , period T and
frequency f=1/T.
, period T and
frequency f=1/T.
It's important to notice that a given harmonic circular motion is fully
described by two independent quantities, the amplitude A (i.e what in the previous
examples we called either xmax or r) and ..... either  or T or f, take
your pick.
or T or f, take
your pick.
In a purely harmonic motion, e.g. a mass on a spring, T and f have an immediate physical
interpretation, while this is not the case for  , as this is the angular velocity of a
fictitious circular motion associated with the harmonic motion at hand. Still, interpreting
harmonic motion as the projection of a uniform circular motion is extremely useful since, with
simple steps (no need for calculus) it allows to derive the proper expressions for both velocity
and acceleration (see derivations in the book):
, as this is the angular velocity of a
fictitious circular motion associated with the harmonic motion at hand. Still, interpreting
harmonic motion as the projection of a uniform circular motion is extremely useful since, with
simple steps (no need for calculus) it allows to derive the proper expressions for both velocity
and acceleration (see derivations in the book):
You are not expected to memorize these expressions, but it is very important that you are aware
of their existence, and that you have a good feeling for what they tell us and how to interpret
them (e.g. what are velocity and acceleration when x = 0, or what is x when the acceleration is at
a maximum, etc. etc., see for instance Conceptual Question 10.8 or Problems 10.41, 10.42).
Combining the expressions above with F = ma alows us to get a very important result
about the period of an oscillating mass-spring system. We have seen that
and
But F = -kx = ma, therefore
i.e. the period of oscillation is determined uniquely by the values of the mass and of the spring
constant. This result is a special case of an extremely important property of vibrating or
oscillating bodies, and is exploited in countless applications. The rule can be roughly
summarized as follows:
when a given body is made to oscillate or vibrate, the frequency of vibration is determined
uniquely by the body's mass/shape/size. In other words,
any object vibrates at its own natural frequency.
A related situation is represented by the pendulum, whose period of oscillation (for
small enough amplitudes, i.e. less than 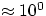 ) can be shown to be
where L is the pendulum length (in general, the distance between the point of suspension and the
center of gravity) and g is the usual acceleration of gravity. This result has obviously been
exploited in numerous applications, going from grandfather clocks to mapping of the earth's
interior.
) can be shown to be
where L is the pendulum length (in general, the distance between the point of suspension and the
center of gravity) and g is the usual acceleration of gravity. This result has obviously been
exploited in numerous applications, going from grandfather clocks to mapping of the earth's
interior.
Energy and Harmonic Motion
Nobody would argue that to compress or stretch a spring requires a certain amount of work, or
alternatively, that a stretched or compressed spring has the ability of doing work, therefore
it possesses a certain amount of energy. These ideas can be quantified in the following way :
suppose you stretch a spring, i.e. you move one of its ends from its initial position x=0 to
a final position x0. The work required to do this is W = F x0 (there is no 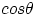 term since force and displacement are parallel). But the problem is that the force is not
constant, in fact at any position x the force is given by F=kx. We could get around this
complication if we knew what the average force is; in this case it is easy to estimate that:
since the force varies linearly with position, the average force is given by the value it has at
the average position x0/2 . In conclusion, the work to stretch a spring by x0 is given by
term since force and displacement are parallel). But the problem is that the force is not
constant, in fact at any position x the force is given by F=kx. We could get around this
complication if we knew what the average force is; in this case it is easy to estimate that:
since the force varies linearly with position, the average force is given by the value it has at
the average position x0/2 . In conclusion, the work to stretch a spring by x0 is given by
W = 1/2kx02
And, by the work energy theorem,this represents the (elastic, potential) energy of a compressed
or stretched spring. It turns out that forces due to springs are conservative, therefore, when
springs are involved, one can thing in terms of conservation of mechanical energy. Putting it
all together, the total amount of mechanical energy a system could have is given by
and, when no non-conservative forces are present (i.e. if the system is subjected only to gravity
and springs) this quantity is conserved.
Probably you will never encounter problems involving at the same time rotations and springs. For
simpler situations, like e.g. spring-driven motion on a horizontal plane, the expression
simplifies to
mv2+kx2 = constant
This, combined with the results we have obtained earlier for the harmonic motion, allows to solve
apparently intractable problems.... like e.g. 10.84 and 10.87
Damped and Driven Harmonic Motions
Under ideal conditions, if a system is put into harmonic motion under the influence of a force
(e.g. the restoring force for a spring, or gravity for a pendulum) it will keep oscillating
forever at a constant frequency and amplitude. In reality, in any realistic situation the effects
of friction, air resistance, etc. will gradually remove energy from the oscillating system and will
bring it to a gradual stop. In such instances we say that the oscillation was damped. And
obviously the time (and the number of oscillations) it takes to bring it to a halt will depend upon
the strength of the damping agent.
In many cases (automobile shock absorber, swinging door, high tech downhill skis, etc.) we want to be able
to dissipate the oscillation energy as fast as possible, in order to bring the system to the equilibrium
position in the shortest possible way. The response of a system to damping will depend on the relative
values of its natural frequency and the damping force. In general, we distinguish the following situations:
- when the system comes to rest after a few oscillation, we say it is underdamped
- the system does not perform even a single oscillation, but it takes a very long time to come back to
equilibrium, this is the condition of overdamping
- an optimal choice of parameters would cause the system to reach equilibrium in the shortest possible
time (and with no oscillations); this is the case of critical damping
In the opposite scenario, we can have a force acting onto a system and adding energy to it.
If the force is acting on an oscillating system in a random way, it will probably not have much of an effect.
Think of a swing : if you give it random pushes, sometimes you will push it when it comes towards you, sometimes
when it's moving away, and the swing will not swing very widely. But if you synchronize
your pushes with the swing's natural oscillation frequency (a swing is like a pendulum, it's frequency of
oscillation is uniquely determined by the location of its center of mass), then you will achieve large
amplitude of oscillations. This effect is called resonance, and its consequences can be quite
spectacular (we will see even more examples when dealing with sound, remember that sound is the audible
result of a vibration).



Next: About this document ...
Sergio Conetti
11/4/1999
![]() or T or f, take
your pick.
or T or f, take
your pick.
![]() , as this is the angular velocity of a
fictitious circular motion associated with the harmonic motion at hand. Still, interpreting
harmonic motion as the projection of a uniform circular motion is extremely useful since, with
simple steps (no need for calculus) it allows to derive the proper expressions for both velocity
and acceleration (see derivations in the book):
, as this is the angular velocity of a
fictitious circular motion associated with the harmonic motion at hand. Still, interpreting
harmonic motion as the projection of a uniform circular motion is extremely useful since, with
simple steps (no need for calculus) it allows to derive the proper expressions for both velocity
and acceleration (see derivations in the book):
![]() term since force and displacement are parallel). But the problem is that the force is not
constant, in fact at any position x the force is given by F=kx. We could get around this
complication if we knew what the average force is; in this case it is easy to estimate that:
since the force varies linearly with position, the average force is given by the value it has at
the average position x0/2 . In conclusion, the work to stretch a spring by x0 is given by
term since force and displacement are parallel). But the problem is that the force is not
constant, in fact at any position x the force is given by F=kx. We could get around this
complication if we knew what the average force is; in this case it is easy to estimate that:
since the force varies linearly with position, the average force is given by the value it has at
the average position x0/2 . In conclusion, the work to stretch a spring by x0 is given by