


Next: About this document ...
Lecture 19
Thermodynamics
The material in this chapter will probably leave you with a sense of dissatisfaction, since you wil be asked
to believe several statements without any convincing proof. Still, these principles have extremely far reaching
consequences for the technological world of today, and it is importnat to have some grasp of them (and it is
also true that many of the concepts, athough their rigorous proof is beyond the scope of this course, are
intuitive to a fair extent). I will also skip some of the details included in the textbook, while concentrating
on the applications.
What we are going to study are the general relations that control the transformation (and the exploitation)
of thermal energy into mechanical work. To do so we will consider thermodynamical systems, i.e.
any suitable choice of objects, machinery (or possibly just a part of a machinery), etc. that interacts
with its surroundings by exchanging energy in either direction (by surroundings we mean everything else in the
universe, except for the components of the system). More specifically:
- at any instant, a system has some internal energy. We have seen how the internal
energy has a particularly simple expression when dealing with a monoatomic ideal gas. In general the situation
might be more complicated, but it will still be true that the internal energy is somehow related to the
(absolute) temperature of the system.
- when interacting with its surroundings, a system can either gain or release a certain quantity of heat
Q. We will adopt the convention that Q is positive when it goes into the system (and negative when it
comes out of it)
- finally in any particular process mechanical work (defined as, remember, Force x Displacement) might be
involved. Our convention will be that work is positive when done by the system, negative when done
onto the system. To clarify with an example: if you have a volume of gas inside a cylinder with a movable piston,
if the gas moves the piston while expanding the work done is positive, but if we compress the gas by pushing
the piston the work involved is negative.
In the past, we have often encountered the principle of Conservation of Mechanical Energy and have seen
that to change the energy of a system some net work must be at play. Next, we have also learnt how there is a
type of energy, thermal energy, that is associated with heat, and in fact a heat transfer represents a transfer
of energy between two systems (or two components of a system). It is then rather immediate to express the principle
of Energy Conservation when applied to thermodynamical systems : we will say that, in any thermodynamical process
there must be a balance between heat exchanged, work done and change in internal energy, i.e.
Q = W +
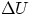
Examples : Problems 15.1, 15.3
The expression above, which is more often written as
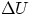
= Q - W
represents the First Law of Thermodynamics. A simple way of expressing it is that you can't get more
work than the amount of heat you put in (unless you deplete the internal energy of the system, which is of
course finite) : there is no perpetual motion.
Thermal Processes, special cases
When studying the ideal gas law, we had already considerd the special cases of processes occurring respectively
at constant pressure, constant volume or constant temperature (they go under the respective names of
isobaric, isochoric and isothermal). Another important (ideal) case is when a thermodynamical system
does not exchange any heat with the surroundings; this process is called adiabatic. What does the First
Law tell us for these cases?
- isobaric process . An example would be our usual gas with the movable piston, with a constant weight
applied to the piston. If we heat the gas (positive Q), in general this will both do some work (move the piston
as the gas expands) and increase the system internal energy. In these cases, the work done is given by a simple
expression : if the volume increase is
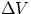 and the piston, of area is A, moves by an amount s, one has
and the piston, of area is A, moves by an amount s, one has
W = F x s = F/A x s x A = P x
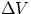
- isochoric process. In this case, it is even more obvious that work is zero, therefore the balance is just
between heat and internal energy : positive Q will increase U (the system will increase its temperature),
negative Q will decrease it. And when dealing with ideal gases, one has P/T = constant.
- isothermic process. In this type of process the system's internal energy remains constant (except for the case of
phase change), and the balance is between work and heat, Q = W. Pressure and volume change accordingly to
PV = constant. A plot of P vs. V will look like the function y = 1/x (this is called a hyperbole).
- adiabatic. When Q = 0, then one has
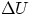 = -W, if the system does positive work it has to do it at
the expense of its own internal energy, and, in general, pressure, volume and temperature will change.
= -W, if the system does positive work it has to do it at
the expense of its own internal energy, and, in general, pressure, volume and temperature will change.
The expression we have found for the work in the isobaric case can be extended to more general cases. The
result W = P x 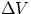 can be interpreted by saying that work is given by the area enclosed in the Pressure
vs. Volume graph. For the general case of non-constant pressure, we could still think of subdividing the whole
process into many smal steps, such that in each step the pressure is almost constant, and for each of these
steps the elementary work will be given by the product P x
can be interpreted by saying that work is given by the area enclosed in the Pressure
vs. Volume graph. For the general case of non-constant pressure, we could still think of subdividing the whole
process into many smal steps, such that in each step the pressure is almost constant, and for each of these
steps the elementary work will be given by the product P x 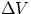 . The total work wil be the sum of the
small pieces, therefore again it will be given by the area under the P vs. V graph.
. The total work wil be the sum of the
small pieces, therefore again it will be given by the area under the P vs. V graph.
Section 15.5 : read and understand the concepts, but ignore formulae 15.3 and 15.5
Section 15.6 : skip
Heat Engines and the Second Law
It would be the subject for an interesting socio-historical study (and maybe someone has done it already) to
understand why, even though the potential of heat (e.g. high pressure steam) to generate mechanical work was
known since antiquity, practical applications did not occur until the 18th century, culminating
with the achievements of the industrial revolution.
Whatever the reason, it is a fact that the
development of the heat engine occurred simultaneously with the formal development of the
corresponding science branch, ie. Thermodynamics, and the two proceeded hand in hand, one advance in one
prompting the next step in the other, as it is often the case in science.
But what is a heat engine? In its first instances, it is a device that converts thermal energy into
mechanical work (today, we might also want to include among heat engines devices like air conditioners and
refrigerators that perform a different task, i.e. they use energy to move heat "the wrong way"). But, as
soon as you think of any traditional heat engine (steam locomotive, gasoline burning car, oil burning power
station, etc.) you soon realize that, in any such applications, not all the thermal energy available at the
input is transformed into mechanical work, but some of it remains in the form of thermal energy (either
e.g. as heat generated by friction or by heat carried away by the exhaust system). Another apparently trivial
consideration (but maybe not as trivial as it might appear) is that the work-producing heat source has to be
at a higher temperature than the heat exhaust. In other words heat does not flow spontaneously from a
colder to a hotter system (this is one of several equivalent ways of expressing the second Law of
Thermodynamics.
But let's go back to our heat engine, and let's assume that it works in some sort of cyclical
way : some amount of heat is given to the engine, which then produces a certain amount of work, it exhausts a
certain amount of heat to the outside, and then gets ready to start another cycle by going back to the initial
high temperature. In a full cycle there is no change in internal energy, therefore
W = Qin - Qout = QH - QC
where we use the indices H(ot) and C(old) to remember the temperature difference between the input and output
heat. If we define as efficiency e of our engine the ratio of work output to energy (i.e. heat) input, we
have
e = W/QH = (QH-QC)/QH = 1-QC/QH < 1
In general, it is not straightforward to estimate how much heat a given engine loses to its surroundings (
friction processes and the like are very hard to quantify), but theoretical studies of cyclical
processes allowed to identify an ideal case representing the best possible theoretical performance a heat
engine could ever achieve. The French scientist-engineer Sadi Carnot investigated the properties of
reversible processes, i.e cyclical processes such that, at the end of the cycle, both the system and
its environment return exactly at the original state (a perfectly reversible process is just an abstract
concept, since it would require that every molecule gets back to its original position and velocity; it is as
if, in an eight-ball pool game, the balls come back to their original position after the breaking).
Anyway the result of this study (i.e. the performance of a Carnot Cycle consisting of the sequence
[isothermal (at temperature TH)-adiabatic-isothermal (at TC)-adiabatic] showed that the quantity
1-QC/QH represents in fact that upper limit of efficiency
that a perfect machine could achieve. Moreover, it was shown that QC/QH = TC/TH, where TH
and TC are respectively the absolute temperatures of the (hot) heat source and the (colder) heat sink.
Consequently, the ultimate limit of efficiency for any possible heat engine is given by
e = 1-TC/TH < 1
This is a remarkable result, since it is independent of the type of machine, the source of thermal energy (steam,
gasoline, etc.) and the process employed to produce work. It also says that the highest efficiency are achieved
for the highest temperature differentials between heat source and sink, with e = 1 only approched in the
(unrealistic and impractical) case T = absolute zero (although this is not too far from what is encounterd in
outer space). From these results follows an alternative way of stating the Second Law of Thermodynamics:
it is impossible to have a system whose sole result is the complete transformation of heat into an
equivalent amount of mechanical work (notice that energy conservation , i.e. the first law , does
allow in principle the processes that are forbidden by the second law). Perpetual motion is even harder than the
first law might have implied !!
Refigerators, air conditioners, etc.
The second law of Thermodynamics tells you that heat does not travel
spontaneously from a colder environment to a warmer one. But
the law does not prevent you from achieving the "wrong direction" heat
transfer by doing some work onto the system. And this is in fact what is
done for refrigerators, air conditioners and heat pumps : in all of these
cases, some amount of energy (typically electric energy, even though it
would be possible in principle to run e.g. a refrigerator with a diesel
engine or even with manual labour..) is used to do the work of transferring
heat from a colder to a warmer environment (and as a consequence, the cold
section becomes colder and the warm warmer). In the three common applications
the cold and warm parts of the system are respectively:
| Device |
Cold Reservoir |
Hot Reservoir |
| Fridge |
fridge insides |
kitchen |
| Air Conditioner |
room |
outdoors |
| Heat Pump |
outdoors |
inside of house |
In all of these cases, the first law of thermodynamics, W = QH-QC, is still valid, but in each
case QH and QC will have different meanings. Also for these devices, the performance is
normally quoted in terms of a coefficient of performance rather than in terms of efficiency.
How is this defined?
For a heat pump, the relevant quantity is the amount of heat brought into the house for a given amount of
work, i.e.
coeff. of perf. = QH/W
Notice that this is just the inverse of the previously defined efficiency (=W/QH). But notice also that,
for a heat pump, we would like "low efficiency", i.e large coefficent of performance. For a perfect (i.e.
Carnot-like) device we also have :
QH/W = QH/(QH-QC) = ...... = TH/(TH-TC) > 1
which shows that the performance does depend on the two temperatures. Moreover, heat pumps do not perform very
well when the outside temperature is too low.
For air conditioners and refrigerators, the relevant performance figure is how much heat can be removed from
the cold reservoir for a given amount of work :
coeff. of perf. = QC/W
And, in a similar way we could see that the ideal performance is given by
QC/W = QC/(QH-QC) = ...... = TC/(TH-TC) > 1
Section 15.11, Entropy : skip



Next: About this document ...
Sergio Conetti
12/3/1999