


Next: About this document ...
Lecture 2
Sign of vector components, general rule : the value of a vector component is given
by the coordinate of the head's projection minus the coordinate of the tail projection.
From this, it follows immediately that a component will be positive if it "points" in the
same drection as the axis, negative if it "points" in the opposite direction.
It is obvious that the sign of the components will depend upon the choice of orientation for
the reference axes. The normal choice is the x-axis pointing to the right and the y-axis
pointing up, but nobody can prevent me from making a different choice (in problems dealing
with gravity and falling bodies, it is not uncommon to have the vertical axis pointing
downwards).
once you make a choice for a given problem, stick with it throughout all the steps,
and evaluate consistently the signs of the various components
Motion in one dimension
We start now the study of MECHANICS, i.e. the branch of Physics that deals with the
motion of objects. Mechanics is traditionally didvided into :
- KINEMATICS : "how" things move
- DYNAMICS : "why" things move
We start with a few, rather trivial, definitions :
These definitions are quite general, and apply to every possible situation. For a while, we will
study motions taking place only along a given direction, let's say along the x-axis. For
simplicity, in this case we will not need to specify explicitely when we are dealing with vector
quantities (the direction is always the same), but let us not forget that quantities like
velocity and displacement can be positive or negative.
If our object is at position x0 at the time t0 at at position x at time t, the above
expression reduces to :
Do remember that this represents the average velocity in the time interval
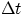 (or the actual velocity, if the object is traveling at a constant, non changing
rate).
(or the actual velocity, if the object is traveling at a constant, non changing
rate).
In general, objects will not move at constant velocity, and we might like to know
their actual velocity at any given instant. Given that 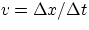 , the smaller we
make the interval
, the smaller we
make the interval 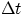 during which we measure the displacement, the closer we get to
measure the instantaneous velocity. Practically, it is impossible to measure the real
instantaneous velocity, but mathematically it is meaningful. The standard definition is
during which we measure the displacement, the closer we get to
measure the instantaneous velocity. Practically, it is impossible to measure the real
instantaneous velocity, but mathematically it is meaningful. The standard definition is
If you have never dealt with Calculus, you might wonder about the meaning of this expression
(what does it mean to divide 0 by 0 ?), but rest assured that the operation is meaningful and it
gives a reasonable result (we will see its meaning in a while). But we can at least state the
following : if an object is moving with constant velocity, then
velocity = average velocity = instantaneous velocity
When dealing with average (or constant) velocities, we can
rewrite the expression above as
x(t) = x0 + vt
where we have assumed that x0 is the position at t=0. This expression summarizes
everything that we can say about motion with constant velocity (or for which only the average
velocity is known), and it allows us to solve any possible problem dealing with such a
situation. We can thing of the expression as containing 4 variables, which means that, known
any 3 of them, we can uniquely find the 4th one.
It is very useful to think of the geometrical interpretation of the expression : it represents
a straight line in the x-t plane. And the slope of the line, geometrically given by
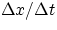 is nothing but the velocity !!!
is nothing but the velocity !!!
Problems dealing with a single object moving with constant velocity are fairly straightforward.
More interesting is the case when we have two objects, each one moving with its own (constant)
velocity, and we are asked to find out where (or when) they meet. To solve these problems, it is
useful to thing of the meaning of the term "to meet" : it means to be at the same place
at the same time. The solution to the problem is then to find the "t" for which the two objects
have the same "x". Specifically, the motion of object 1 is given by x(t) = x01 + v1t,
and object 2 by x(t) = x02 + v2t. If, at any time, they are at the same "x", we must
have
x(t) = x01 + v1t = x02 + v2t
v1t - v2t = x02-x01
t = (x02-x01)/(v1-v2
which gives the "meeting time". Substitution in either of the x(t) expression will
give me the meeting place... Notice that the expression we have found for t will always have a
unique solution, as long as 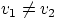 .... What is the graphical interpretation of the
problem ? It is that of two straight lines in the plane, that will always intersect in one point,
unless they are parallel...
.... What is the graphical interpretation of the
problem ? It is that of two straight lines in the plane, that will always intersect in one point,
unless they are parallel...
Motion with constant Acceleration
Now that we know how to handle constant velocities, we can attack the case of variable
velocity. Whenever there is a change in velocity, we will say that there is an
acceleration.
Let us suppose that an object has a velocity v0 at time t0 and v at time t. We will say that its
(average) acceleration was
(Note that, as we are still working in one dimension, I am not using the vector nomenclature, but let
us not be confused : in general acceleration, as given by the difference between two vectors divided by
a scalar, is itself a vector)
Acceleration expresses the change of velocity in a given time, therefore it will be measured (in the
SI system) in meters per second .... per second = (m/s)/s = m/s2, or any other equivalent
unit. Dimensionally,
[acceleration] = [L/T2] = [LT-2].
Note : in common language, one talks about accelerations and decelerations, and one might even be
inclined to think that a deceleration is a "negative acceleration". This can be misleading, and it is
better to think in the following terms :
we have a real acceleration (i.e. the velocity is increasing) when acceleration and velocity point in
the same direction (i.e. they have the same sign). Velocity will decrease (i.e. we are "decelerating")
when velocity and acceleration have opposite signs
In analogy to what was done earlier, we can think in terms of average acceleration (if we only know the
initial and final conditions) or, when the acceleration is continuously varying, of instantaneous
acceleration, which, will be defined as previously :
Throughout the course, we will almost always limit ourselves to the case of constant (or average)
accelerations. For this case we have immediately :
v(t) = v0 + at
whwre we have assumed that, at t=0, the velocity is is v0. Notice the formal identity between the
expressions relating time and displacement (for the case of constant v) and time and velocity (for the
case of constant a). The procedures we have learnt for the former situation can be transported to the
latter.
But this is not enough, to describe the motion fully we must be able to say something about displacement.
Here is how we can do it : to start, we know how to find the displacement if we know the average
velocity :
x = x0 + vavt
But, in our case of constant acceleration, what is the average velocity? let us say that we start at t=0
with a velocity v0 and at time t the velocity is v. We have just seen that v(t) = v0 + at.
The average velocity will then be the midway value between initial and final velocity:
vav = (vfinal + vinitial)/2 = (v0 +at + v0)/2 = v0 + at/2
Substitution into the expression for x gives :
x(t) = x0 + v0t + 1/2 at2
This expression, together with v(t) = v0 + at, is all that you need to fully describe the
rectilinear motion with constant acceleration, and allow you to solve any possible problem.
Notes :
- 1.
- In addition to the two above, other formulae can be derived from them (textbook formulae 2.7 and
2.9). I do not believe in trying to memorize too many formulae, I think it is better to know the few
fundamental ones, and derive other formulae and/or quantities as the need arises
- 2.
- in formula 2.8 (the equivalent of my expression for x(t)), the book omits the term x0. This
is probably unwise, since it is not always possible to assume that x=0 when t=0, especially when
facing problems dealing with more than one body. And in fact, in Example 11 (page 43) the book makes
non-explicit use of a term x0
Graphical interpretation : the expression giving velocity as a function of time is, as before, a
straight line in the v-t plane. The (constant) slope of the line is the (constant) acceleration.
The expression for x(t) is quadratic in t. In the simplest case x0=v0 = 0,the curve is a
parabola symmetric around the origin. Remember how in the case of constant velocity, the velocity was
given by the (constant) slope of the x vs. t line. This is still true even for the the non-straight
case of constant acceleration : the velocity, which is continuously changing, is given by the
local slope of the curve, i.e. the tangent to the curve at any given point.
In general, a parabola and a straight line will meet in two points (when they do meet). This means that
problems involving the "meeting" of two bodies, one moving with constant velocity and one with constant
acceleration will have two solutions,which might not always be real (see e.g. Example 11). Such problems
are solved as before, i.e. finding the conditions for which the two bodies are at the same place at the
same time.
Freely Falling Bodies
In order to study the motion of freely falling bodies, we only need to know one fact : a body falling
freely under the effect of gravity experiences a constant acceleration "g" directed downward.
g is known to be, on earth , about 9.80 m/s2.
The fact that all bodies fall at the same rate, might be counter-intuitive at first thought (for many
centuries, following Aristoteles ideas, "philosopers" would have sworn that heavier bodies fall faster).
But on second thought, it is more logical to believe that all bodies fall at the same rate. Nice
conceptual example ("gedanken experiment") by Galileo : take a heavy and a light ball, we are told that
the light one will fall more slowly. But now attach them together with a very thin thread : the light ball,
by its intrinsic lower rate of falling, should retard the fall of the heavy one...But,on the other side,
the combination of the two balls is heavier than each single one, so they should fall even faster....
We are then facing an absurdity, and the way out of it is to assume that all bodies fall at the same rate.
But, if you still have any doubt, you can just do some clever
measurement. This is what Galileo did, and this is why he is considered the father of modern science:
it is not just enough to have a nice theory, but you must verify whether it agrees with the data. If it
doesn't, and your measurements were done right, then you must as well throw away your theory and go back
to the drawing board....
But we are digressing, coming back to a free falling object, it is a fact that, by means of the formulae
we have
just learnt, we can completely describe its motion i.e. we can predict, at any instant its velocity
and position (provided we know the initial conditions).
It is also useful to think of the graph of velocity vs. time of an object tossed up in the air...
Some results can be surprising at first, but with good reasoning everything makes sense. I find Example
18 particularly instructive :
a shotgun fires a pellet either straight up or straight down. In either case the magnitude of the initial
velocity, as the pellet leaves the gun, is the same. In which case will the pellet hit the ground with
higher velocity ?
To answer the question, we will find out the velocity of the upward going pellet when it comes back to
its starting point.
The counter-intuitive result (the final velocity is the same) will be less surprising when we learn
about Conservation of Energy, in a few weeks.



Next: About this document ...
Sergio Conetti
9/8/1999