Lecture 20

Waves

We will call wave a disturbance in a medium propagating through it. The effect of a wave is to transmit a certain amount of energy (in most cases kinetic energy) from one place to another. But notice that the transport of energy occurs without any net displacement of the medium's matter. As a wave goes through, particles of the medium oscillate up and down (or back and forth) around their position of equilibrium. When dealing with a wave we should then distinguish between the motion of the actual wave (i.e. its velocity and its direction of propagation) and the motion of the medium's elements. In particular we distinguish between

• transversal waves, when the medium oscillates in a direction perpendicular to the direction of wave propagation
• longitudinal waves when oscillation and wave propagation are parallel to each other

Sea waves are apparently a good example of transversal waves, even though a closer analysis would show that they are in fact a mixture of both longitudinal and transverse, since, in a wavy sea, individual water molecules move in a sort of circular pattern.

A wave can consist of just a single traveling disturbance (e.g. the wake of a motorboat) or, in the more interesting case, of a train of successive pulses. In this case, a complete description of the wave requires to define its behaviour both in terms of variation as a function of position and as a function of time. Specifically (thinking e.g. of a regular pattern of sea waves) we could look at the wave pattern at a single moment in time (i.e. as if we were taking a snapshot of it), and we would see something resembling a sine function. In other words, at a given instant in time the y (i.e vertical) position of al the water particles could be described by

$y~=~A\sin (2\pi x/\lambda)$

(in writing this expression, we assume that the wave is actually well represented by a sine function; it turns out that this is in fact the case for a large class of phenomena). The meaning of $\lambda$, the wavelength is quite obvious : from the expression above, $\lambda$ represents the distance after which the wave repeats itself, therefore it is the distance between two points of equal displacement (e.g. the distance between two crests).

On the other side, we could just concentrate on a given location in the medium (i.e. a given x), and study how its y position varies as a function of time (i.e. as the wave goes through). At one location, under the effect of the wave a given particle will go up and down (if we are dealing with transversal waves), in a harmonic-like behaviour. If the motion is truly harmonic (as it is the case for a large class of phenomena), the y displacement at a particular location, as a function of time, will be

$y~=~A\sin (2\pi t/T)$

where T is , as usual, the period, i.e the time to perform one complete oscillation. We could also replace the period with its inverse, the frequency, i.e. the number of full oscillations completed in the unit time, and write

$y~=~A\sin (2\pi ft)$

Combining the two together, we obtain the expression describing the global wave behaviour:

$y~=~A\sin [2\pi( t/T \pm x/\lambda)]~=~A\sin [2\pi( ft \pm x/\lambda)]$

where the + or - sign will depend on whether the wave is progressing respectively towards the negative or positive x direction (why does the - sign correspond to a motion in the positive x direction?).

We then see that a (periodic, harmonic) wave is described by three quantities, the amplitude, the period (or frequency) and the wavelength. What about the velocity of wave propagation? It is immediate to see that it is fully determined by two of the above quantities. The reasoning is the following : velocity is, as usual, the ratio between distance covered and time to cover it. Let us concentrate on a point in the wave where, at t=0, there is a crest. After a time T, at that point there will be the successive crest; in other words, in the time T the wave moves by the distance between two crests, i.e by an amount $\lambda$. We then have

v = $\lambda$/T = $\lambda$f

This is a very fundamental relation applying to all harmonic waves, e.g. radio (=electromagnetic) waves, see example 1.

From the expression just found, we can see that, in any given situation, velocity, frequency and wavelength cannot all three be chosen arbitrarily, but, once two are given, the third is uniquely determined. Moreover, when a wave propagates through a medium, its velocity of propagation is fully determined by the physical properites of the medium. Therefore, if we generate a wave by means of a periodic pulse (which effectively fixes the frequency) and this wave train propagates through a given medium, then the wave's wavelength is fully determined. A common situation is that of a wave propagating along a stretched string or rope. In this case, it could be seen that the velocity of wave propagation is given by

v = $\sqrt{lF/m}$

where l is the string's length, m its mass and F the tension : waves propagate faster through a tight string than through a slack one.

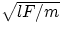
Sound waves

Particularly interesting waves are sound waves. When an object vibrates, it transmits its vibrations to the air surrounding it: as an example, hitting a drum causes its membrane to vibrate back and forth, and, in doing so, it produces successive regions of higher and lower pressure in the air around it. These pressure waves propagate through the air and, if they reach an ear, they induce the same vibration in the eardrum. The eardrum vibrations are then interpreted by the brain as sound, and the pitch of the sound is determined by the vibration frequency. Human ears are sensitive to vibrations in the approximate range 20 (very low pitch) to 20,000 (very high pitch) Hz (1 Hz = 1 hertz = 1 vibration per second). Any given sound in general consists of the superposition of many different waves of different frequencies but, in some particularly simple case, one can just have a single frequency (called a pure tone).

Frequencies below the audible range correspond to infrasounds, above it to ultrasounds (notice the similarity with visible light, infrared and ultraviolet, but do not confuse electromagnetic waves with sound waves, they are completely different phenomena, even though they are both waves).

To generate sound, vibrating objects transmit their vibrations to a medium (it doesn't have to be air, sound propagates equally well through liquids and solids), but sound will not exist in a vacuum : Star War movies portraying battles in outer space should save money and not hire a sound effect specialist, since such battles would be accompanied by eery silence...

Section 16.6 : you can ignore formulae 16.5, 16.6, 16.7 and the relative discussion, it is sufficient if you are aware of the following facts :

• speed of sound depends strongly on the medium through which it propagates
• sound speed is the smallest in gases, followed by liquids and then solids
• in air (at 20⁰C) sound speed is about 340 m/s (that is roughly 1 mile in 5 seconds)
• sound speed depends on the medium temperature, in gases sound speed is proportional to $\sqrt{T}$
  
  

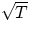
Question (conceptual question 16.11): remembering that v = $\lambda$f, what happens to a sound wave when it goes from one medium to another of different sound velocity? Does the wavelength change, or the frequency or both?

Sound Energy

Waves do carry energy, and so does sound. The energy emitted by any sound source will, as usual, be measured in joules and the energy emitted per unit time in watts. But, when dealing with sound, one is usually interested in how much of the sound power is detected by a receiver of a given area positioned at a certain distance from the source. We define as sound intensity I the amount of sound energy received per unit time (i.e. the power) per unit surface

I = P/A

which will be obviously measured in W/m². One can immediately see that the Intensity of sound decreases like the inverse square of the distance from the source: suppose that a sound source emits a certain amount of power P, and the emission is uniform in all directions. At a distance r from the source, the sound energy will be spread equally over the surface of a sphere centered at the source (area of sphere = 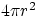$4\pi r^2$), so that the intensity will be :

I = P/A = P/(4$\pi r^2$)

The human ear can detect sound intensities as low as 10^-12 W/m² (animals with big ears can detect even lower intensities), and it can tolerate (with pain) intensities that are more than 1 million million times stronger, therefore corresponding to a few W/m². Given this very wide range, one can guess that the ear response will not be linear : a sound of 1000 times the intensity will not be perceived as 1000 times louder. Because of the non-linear response and the very wide range, it is customary to compare sound levels on a logarithmic scale (this is the time to review Appendix D). Specifically, one expresses the loudness of a sound of intensity I by comparing it with the threshold of hearing I₀ by means of decibels, defined as

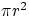
decibel = 10 log₁₀ (I/I₀)

(the factor of 10 in front is there since the primitive unit, that hardly anyone uses, is the bel, with 1 decibel = 1/10 of a bel, therefore (value in dB) = 10 x (value in bels)). The reason for using decibels is that it has been shown that 1 dB is roughly the smallest change in sound intensity that a normal human ear can detect. To what change in intensity does this correspond ?

1 = 10 log₁₀ (I₂/I₁)

1/10 = log₁₀ (I₂/I₁)

I₂/I₁ = 10^1/10 = 1.25

showing that a change of one decibel correspond to an intensity increase of about 25%.

Doppler Effect

The Doppler effect, describing how the frequency of a wave is modified when either the wave source or the wave detector are in motion, has been exploited in an ever incresing number of applications, rangig from measuring the speed of blood flow to determining the age of the Universe; the next time you are caught speeding by the police radar, you can blame Herr Doppler. For now, we will limit ourselves the study of this effect when dealing with sound waves.

Suppose that a sound source emits a signal with a constant frequency f : this means that, in every second, the source generates f sound waves. A listener at a certain distance from the source, will also receive f waves per second, and will interpret this as a sound of a given pitch. But suppose now that the sound source is moving towards the listener (at a speed less than the speed of sound). Now the distance between separate sound waves. i.e. the wavelength, will decrease since, after it emits one wave, the source moves (from the point of view of the listener) in the direction of the wave it has emitted. Numerically, if v is the speed of sound and w the speed of the source, during one period T, while one wave moves by the quantity vT, the source moves by an amount wT, so that the distance between the two waves (e.g. between the two crests of the waves) is

$\lambda '~=~(v-w)T$

Our listener will then receive, in the unit time, a larger amount of waves, therefore the sound he perceives will have a higher frequency (higher pitch) f', according to

$f'~=~v/\lambda '~=~\frac{v}{T(v-w)}~=~f\times v/(v-w)~=~f/(1-\frac{w}{v})$

Similar reasoning would show that, when the source is moving away from the listener, the distance between waves increases, and correspondinlgly a higher frequency (lower pitch) is detected, according to

$f'~=~f\times v/(v+w)~=~f/(1+\frac{w}{v})$

Similar phenomena will occur when the source is stationary and the listener moves away from or towards it. If by w now we mean the listener's speed, the result one would obtain is

$f'~=~f\times(1\pm\frac{w}{v})$

where the + sign is for an approaching listener (higher pitch) and the - for the listener moving away.

Wave Interference
If you are running, and bump into another runner, you are likely to suffer some lasting consequences. Waves, on the contrary, have the remarkable property that, when meeting another wave, do undergo some temporary perturbation, but then continue their travel unperturbed. But what is the perturbation when they meet? Very simply, the result of two crossing waves is, at every point, the algebraic sum of the wave amplitude. The final effect will then depend on the relative phase of the two crossing waves. What do we mean by phase ? Thinking of a wave as described by a sine function, the phase is the argument of the sine (in the general equation of the wave we have studied, the phase would be the numerical value of the quantity 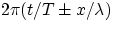$2\pi (t/T\pm x/\lambda)$). Another useful way to interpret the meaning of phase is to remember that a harmonic motion can be interpreted as the projection of a uniform circular motion. In this case the phase angle is just the angle around the circle.

But coming back to our crossing waves, one possibility is that, when they meet, they are perfectly in phase, i.e. when one wave has a crest so does the other, etc. In this case, as they meet the two waves reinforce each other, giving raise to a wave of twice the amplitude. We call such an occurrence fully constructive interference. At the opposite extreme, the waves could meet while fully out of phase, i.e. when one has a crest the other has a trough. The two waves will then end up cancelling each other, and we will witness fully destructive interference. For any other intermediate possibility, the interference will be only partially constructive or destructive.

If we have two wave sources generating identical waves, can we predict at what locations we might encounter fully constructive or destructive interferences? The simple answer is that this will happen when the difference in distance of the listener from the two sources is either an exact number of wavelengths (fully constructive) or a half integer number of wavelengths (fully destructive).

Beats

Another interesting phenomenon occurs when two sound sources are producing waves of nearly (but not exactly) the same frequency. A good way of picturing such a situation is to think of two runners racing around a circular track at slightly differing speeds. Their relative position will change all the time but, periodically, they will find each other either in exactly opposite locations (i.e. 180⁰ out of phase) or at the same location, i.e. in phase.

Two waves of slightly different frequencies will behave the same way: periodically they will be either fully in phase, and the sound intensity will reach a maximum, or out of phase, with consequent almost vanishing sound. It could be seen that the absolute value of the beat frequency, i.e. the frequency of, e.g., maximum amplitude, is given by the frequency difference between the two sources.