


Next: About this document ...
Lecture 3
Motion in two Dimensions
If you master the equations of motion in one dimension, you are in
very good shape, since you will be able to handle any problem in
any number of dimensions (even though we will limit ourselves to
the case of two dimensions only).
The rule is very simple : what happen in x is independent of what
happens in y. We can solve any problem by writing down the
projections of the equations of motion on the x and y axis respectively,
and solve separately in x and in y.
Formally : if 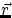 is the displacement vector in the x-y plane,
the equations of motion (for the case of constant acceleration a) are
written as:
These are equations among vectors, that we would not know how to solve.
But what we can do is to project the vectors on the two axes, to get:
is the displacement vector in the x-y plane,
the equations of motion (for the case of constant acceleration a) are
written as:
These are equations among vectors, that we would not know how to solve.
But what we can do is to project the vectors on the two axes, to get:
x(t)=x0+v0xt+1/2 axt2, y(t)=y0+v0yt+1/2 ayt2
vx(t) = v0x+axt, vy(t) = v0y+ayt
and these we know how to handle.
The most common case,encountered in endless situations (kicking a football,
dropping a package from a plane, throwing a stone off a cliff, hitting a
golfball, doing the long jump, etc., etc.) is that of a body with a
given initial velocity  (whose components are
(whose components are 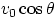 and
and 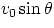 ), that is subjected to the acceleration of gravity. The
most important thing to remember for these situations is that
the horizontal motion will continue unperturbed with constant velocity
), that is subjected to the acceleration of gravity. The
most important thing to remember for these situations is that
the horizontal motion will continue unperturbed with constant velocity
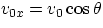 . For the acceleration, one has obviously
. For the acceleration, one has obviously
ax = 0, ay=g
(but pay attention to the sign of g...) In other words the equations of
motion are :
x(t)=x0+v0xt, y(t)=y0+v0yt+1/2 gt2
vx(t) = v0x, vy(t) = v0y+gt
As an immediate application, we get the range of a projectile : suppose
you hit a golf ball, giving it an initial velocity 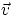 (of magnitude
v) and at an angle
(of magnitude
v) and at an angle 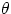 , and we want to find out how far it will go.
The reasoning is that the furthest x will be reached when y=0, i.e. when
the ball hits the ground. We can then write :
, and we want to find out how far it will go.
The reasoning is that the furthest x will be reached when y=0, i.e. when
the ball hits the ground. We can then write :
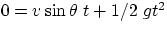
, i.e.
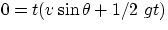
This expression is 0 for either t=0 (which is obviously true) or for
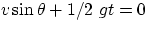
, i.e.
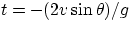
This would give me the "time of flight" of the ball, but I want to know
how far it goes. Substituting in the expression for x, we get:
(remember : 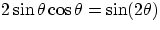
Question : do we have a sign problem ????
General conclusion : the range is proportional to the square of the initial
velocity and, for a given velocity , is the largest for 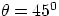 .
.
Famous problem : the monkey and the hunter. A monkey drops a coconut and,
at the same instant, a hunter shoots his gun,trying to hit the nut.
Question : in which direction should the gun point ? You might think that
the answer depends on the distance to the tree and the bullet initial
velocity, but it turns out that the solution is independent of all that,
and you wil hit the target provided you aim at it at t=0. (See also problem
2.47)
Proof :
As usual, hitting the target with the bullet means that target and bullet must
have the same x and y at the same time. Let us choose as positive x the direction
from the gun to the tree, and positive y pointing up. We set the gun at x=y=0, and
the target (coconut) at x0 and y0. If the bullet is shot at an angle 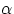 and velocity of magnitude v, the equations of motion for the two objects are
(we write explicitely the minus sign to indicate that g is pointing downward) :
and velocity of magnitude v, the equations of motion for the two objects are
(we write explicitely the minus sign to indicate that g is pointing downward) :
- bullet :
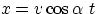
,
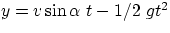
- coconut :
x = x0, y = y0-1/2 gt2
(the coconut obviously remains always at the same x=x0, it only moves in y)
We now impose the condition of y equality :
This gives us the time t at which the two bodies are at the same y, and it will
have to be plugged into the expression for the equality of x, which is :
But 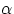 is the direction (until now undetermined) at which the gun was pointing.
And y0/x0 is exactly the tangent of the angle formed by the line joining the gun
with the coconut . The result we have obtained then tells us that the only condition we
need to satisfy is that, at t=0, the gun points at the target.
is the direction (until now undetermined) at which the gun was pointing.
And y0/x0 is exactly the tangent of the angle formed by the line joining the gun
with the coconut . The result we have obtained then tells us that the only condition we
need to satisfy is that, at t=0, the gun points at the target.
Relativity of Velocities
Would you be able to play Table Tennis if the ball were moving at 500 miles/hour?
The answer is yes, provided also you and the table move at the same speed. And this
is what actually happens if your game takes place while flying on a jet-plane :
with respect to the ground, the ball is moving at a few hundred
meters/sec (plus or minus 1 or 2 m/s as it goes back and forth). But of course you are
not aware of it since you are moving at high speed too.
The lesson we learn is that velocity is not an absolute, but a relative
quantity. You probably associate the concept of relativity with Einstein, but relativity
was a familiar concept in Physics well before him. In fact, the concept of relativity
of velocities goes under the name of Galileian Relativity (what Einstein did,
was to show that not only space, but also time is relative).
In a large class of problems, we face a situation where there are several objects in
motion with respect to each other, and we need to determine their relative velocities.
The problem is simpler if we need to determine velocities with respect to something
which appears to be at rest. Examples :
- the velocity of the ping-pong ball with respect to the ground, is the (vectorial)
sum of the velocity of the ball w.r.t. the plane + the velocity of the plane w.r.t.
the ground
- the velocity of a boat in a river is the (vectorial) sum of the velocity of the
boat w.r.t. the water + the velocity of the water w.r.t. the shore
- the velocity of a point on a car tire w.r.t. the ground is etc. etc....
The problem is only a little bit trickier if we have to find the relative velocity
between two objects that are both in motion, e.g. two cars moving towards each other.
A good way to attack such a problem is to pretend that one of the two objects (cars)
is at rest, and perform the vector sum of the other velocities. Specifically :
car A is moving with velocity  and car B with velocity
and car B with velocity 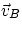 (both
velocities referred to the ground). Question : what is the velocity of B w.r.t. A?
(both
velocities referred to the ground). Question : what is the velocity of B w.r.t. A?
To find the answer we pretend that A is at rest : the answer we look for will be given
by the (vector) sum of the velocity of the ground w.r.t. A + the velocity of B
w.r.t. the ground.
The second term is known, what is the first one ? You should convince yourself that
the velocity of the ground w.r.t. A is the vector opposite to the velocity of A w.r.t.
the ground, i.e. 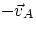 .
.



Next: About this document ...
Sergio Conetti
9/10/1999
![]() (whose components are
(whose components are ![]() and
and ![]() ), that is subjected to the acceleration of gravity. The
most important thing to remember for these situations is that
the horizontal motion will continue unperturbed with constant velocity
), that is subjected to the acceleration of gravity. The
most important thing to remember for these situations is that
the horizontal motion will continue unperturbed with constant velocity
![]() . For the acceleration, one has obviously
. For the acceleration, one has obviously