Lecture 5

We have seen that :

$\vec{F}= m\vec{a}$

Like others we have met before, this is an equation between vectors. As usual, for any particular situation we can get a feeling for the main features of the problem by means of a graphical procedure but, if we want to solve the problem numerically, we have to work with the vector's projections. Specifically, we should solve separately the equations describing the components of the forces and accelerations on the x,y axes and then, if necessary, recombine them to get the global direction of motion.

Examples : problems 4.12, 4.15

Newton's third law

The last general rule we need to know about forces is again a generalization of a common observation. Think of pushing on a wall : you are definitely exerting a force on the wall, but you also feel a pressure on your hand; the wall is therefore exerting a force on your hand. Similarly, if you kick a ball (think of kicking a bowling ball with your bare foot), you will feel for sure that, while you are exerting a force on the ball, the ball gets back at you. These are all examples of Newton's third Law (also called action and reaction), that states :

whenever an object A exerts a force on an object B,
B will exert a force on A
which is equal and opposite to the force exerted by A

It is by way of this principle that we can understand how a rocket can move in outer space even in the absence of an atmosphere. It is for a fact that, as recently as a few decades ago, people (rocket scientists?) that did not know their physics claimed that outer space rocket propulsion was impossible since out there there is no air, and the rocket has nothing to push itself against.

But the correct reasoning is the following : when a rocket engine emits a jet of fast gas, it obviously exerts a force on the gas. But, by Newton's third law, the gas will exert an equal and opposite force on the rocket, and this force can accelerate the rocket.

But applying the third principle correctly can be tricky, here is a thought provoking example : suppose I try to move a cart by pushing on it, the cart is going to push on me with equal and oppsite force, and we will not go anywhere .....

it is useful to solve the quandary by thinking of two different situations :

1.

suppose you are in outer space, far from any other force. If you give a shove to some heavy object, you will put it into motion, but you will also recoil in the opposite direction (this is a nice demonstration of Newton's third law).

2.

but now let's come back on earth, you know that if you push the cart (and it is not too heavy) you will be able to keep it going. Why are you not recoiling backward?

Because of the friction of your feet on the ground .... (in fact you would not be able to push the cart if you were on an icy surface, wearing Teflon shoes like a curling player...)

We then realize that, to understand a problem, we must include all the forces acting on a body : in our case the cart exerts a force on the person; this force is transmitted from the arms to the feet (by the muscle and bone structure) so that the feet push backwards on the earth. But then, by Newton's third law, the earth pushes forward on the feet : if this forward force is larger than the one needed to move the cart, then the cart will move.

Solving problems dealing with Newton'e third law can at times be tricky, especially if you forget the following rules :

1.

when studying the motion of a body, do take into account all the forces acting on it, BUT

2.

do not confuse between forces that are applied to the body and forces that the body applies to others : the two forces that are mentioned in Newton's third law are not applied to the same body

The Gravitational Force

In the second lecture, I had asked you to believe that, as long as we can neglect air resistance, all bodies fall at the same rate, regardless of their mass. Now we are going to understand how this comes about. The result is an immediate consequence of Newton's law of universal gravitation. The term "universal" is relevant: Newton's great achievement was to realize that the apple falling to the ground and the moon orbiting the earth are two different manifestations of the same underlying phenomenon, i.e. the (gravitational) force exerted by the earth on either object. Moreover (and this was maybe an even bolder step) Newton suggested that such force of gravity is felt between any two objects with non-zero mass. And, Newton told us, the magnitude of the force is proportional to the masses of the two bodies, and inversely proportional to the square of their distance, i.e.

F_gravity = G m₁ m₂/r²

where G is a constant that has to be determined experimentally, and whose value will depend of course on the units we choose to measure F, m and r. In the SI system, G turns out to be $\approx 6.67 \times 10^{-11} m^{3}s^{-2}kg^{-1}$.

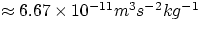Can you figure out why G is measured in m³s^-2kg^-1 ?

Now we can immediately understand why all bodies fall at the same rate : from Newton's law we know that a body of mass m, subjected to a force F will have an acceleration a = F/m . But in this case we know what the force F is, it is the one we just saw, so that we can write, if M is the mass of the earth :

$a = G mM/r^{2} \times 1/m = G M / r^{2}$

and, for a given r, this is a constant.

A qualitative way to convince ourselves that all objects fall at the same rate is the following : a more massive objects will feel a stronger gravitational force but at the same time, being more massive, it will oppose more resistance to being accelerated (it has more "inertia); the two effects cancel each other and everybody ends up with the same acceleration.

There still might be a question on what one should choose for r (i.e. the distance between the two objects). Newton gave the correct answer, but before he could do so he had to "invent" Calculus : when dealing with a spherical homogeneous body, it is as if all of its mass is concentrated in a point at its center. To calculate the above expression, r should then be the distance from the object to the center of the earth (i.e. the earth radius, if the object is at sea level). Which also means that the force of gravity is different between sea level and higher altitudes. Also it is not the same in different locations on earth : if I stand on top of a huge underground cavity, I will feel less force. This minute variations in the force of gravity (and consequently of g) can be used by geologist to study the interior of the earth.

We are now ready to understand the difference between weight and mass : we define as weight the force felt by an object of mass m because of gravity. Weight is therefore a force, and, in the SI system, should be measured in newtons (or in pounds in the British system,since the pound is a unit not of mass but of the weight force). And from what we have just said, given that the force of gravity is not the same everywhere, the weight of an object will change with altitude, location on earth, etc. And if you go through a strict diet and shed a certain amount of fat, you are not really losing weight but losing mass. But of course weight is proportional to mass, so I can use either term.

But what is the relationship between weight and mass? Remember the definition: weight is the Force felt by a body because of gravity, therefore

w = F_gravity = ma

But what is the acceleration in this case ? It is g, so that we can write

w = mg

i.e. the weight, measured in newtons, is 9.8 times the mass (measured in kg). Let me stress again that weight is not a constant property of a body, but mass is : wherever you go, whatever you do, the mass of a body is always the same (at least until we meet Mr. Einstein).