Solutions to static and dynamic examples shown in class:

1- Static case : a hanging mass m₃ is balanced by two masses m₁ and m₂ connected to m₃ by means of strings and pulleys. Given that the system is in equlibrium, then the net force acting on any one point must be zero. This means that both x and y components of the net force must be zero. Applying this condition to the point where the 3 strings come together, the forces acting on that point are the Tensions of the three strings. We can then write
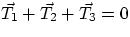$\vec{T_{1}}+\vec{T_{2}}+\vec{T_{3}} = 0$, which can be written, in terms of vector components
T_1x+T_2x+T_3x =0 and T_1y+T_2y+T_3y =0
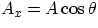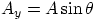(note that any of the cmponents can be either positive or negative, the actual signs will be determined upon choosing the axes orientation). The next step is to write the equations above in terms of tension magnitudes and angles , according to the general rule $A_{x}=A\cos\theta$ and $A_{y}=A\sin\theta$. The two equations will then contain 5 variables, the magnitude of the three tensions and the two angles of the strings 1 and 2. But the magnitude of the tensions are known : looking at the points where each string conects to its mass, one has (in magnitude)
T₁ = m₁g,T₂ = m₂g,T₃ = m₃g, (This is because, as each point is at rest, the forces must cancel, and the forces acting at the point where the string connects to the masss are the mass weight and the string tension). The two equations therefore can be solved, since they contain only two unknowns, i.e. the two angles.

Dynamic case : two masses M and m connected by a pulley. with what acceleration do the masses move? The important things to notice are :
1- the tension of the string is the same everywhere
2- given that the two masses are moving together, the acceleration is the same for both masses in magnitude, but opposite in sign (one mass is moving up and the other is moving down. Notice that this case is different from that of a body tossed up in the air: for the tossed body, the acceleration g has always the same sign (pointing down), regardless of whether the body is going up or down. But, for the two masses, one is accelerating upward and the other downward, therefore their accelerations are opposite in sign). Choosing the positive axis to point up, and applying Newton's law separtely to each mass, one has
-Ma = T - Mg and ma = T - mg, i.e T = Mg - Ma = mg + ma, which can be solved for a, to give
a = g(M-m)/(M+m).

Lecture 7

Uniform Circular Motion

So far, most of the motions we have considered were on a straight line. Now we will consider a very important and useful situation, i.e. the case of an object moving with constant speed on a circular trajectory. Notice that I said speed, and not velocity, since by definition, if the body is changing its direction, the velocity cannot be constant. Which also means that, by definition, if the velocity is changing there must be an acceleration...Which also means that, if there is an acceleration there must be a force... In the following, we will examine the forces and accelerations that come into play when dealing with Uniform Circular Motion.

Note : I will not go through the arguments to derive the expression for the acceleration present in uniform circular motion : a correct, rigorous derivation would require the tools of Calculus, while a semi-rigorous semi-intuitive derivation is given in the book (page 133), and I could only repeat (with more or less clarity) the same arguments. But it is of fundamental importance to know the final result and its consequences

So here is the final result : In order to keep a body moving with velocity of constant magnitude v along a circular path of radius r, an acceleration is required of magnitude v²/r and of direction pointing, at any instant, from the instantaneous position of the body towards the center of the circle.

From the above statement we can also infer that

1.

the acceleration is also non-constant; more precisely, the magnitude is constant, but the direction varies continuously, rotating around the circle like the hand of a clock (either clockwise or counterclockwise)

2.

remembering that, at any point of a circle, the tangent and the radius are perpendicular to each other, and that, for a body moving along a curved trajectory the direction of the instantaneous velocity is given by the tangent to the curve, we can conclude that, when dealing with uniform circular motion velocity and acceleration are, at every instant, perpendicular to each other.

In view of the fact that the circular motion acceleration always points towards the center, it is given the name of centripetal acceleration.

a_c = v²/r

Useful (?) piece of information : in previous lectures, we have dealt with accelerations parallel to the velocity, and we have learnt how they have the effect of changing the magnitude of the velocity. Now we encounter an acceleration perpendicular to the velocity, and we are told that its effect is to change the direction of the velocity, but not its magnitude. These concepts can be generalized :

take a body moving with arbitrary velocity, and apply to it an arbitrary acceleration. Regardless of the relative orientation of the two vectors, it is always possible to separate the acceleration into its component parallel and perpendicular to the velocity. It turns out that the parallel component will always and only be responsible for changing the magnitude of the velocity, while the perpendicualr component will always and only be responsible for changing the velocity's direction.

Other useful facts : when dealing with uniform circular motion, given that the speed is constant, it will always take the same time to cover one full circumference. This time is called the period, T. One has immediately :

v =distance/time = $2\pi r/T$

$a_{c}= v^{2}/r = 4\pi^{2}r/T^{2}$

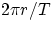
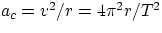
(No "two-star" problems in this section. Problem 6.8 is interesting, try solving it, it is also the starting point towards understanding why the air circulation around a low pressure is counterclockwise)

Centripetal Force

Where there is an acceleration there must be a force. If a body moving with uniform circular has a centripetal acceleration a_c, this acceleration must be the effect of a centripetal force, with the same direction as the acceleration and of magnitude

F_c = mv²/r

where m is the mass of the rotating body. In a given situation of rotational motion it might not always be clear where the centripetal force is coming from, but you can be sure it is somewhere there. Another interesting fact is that a fast rotation can pretty soon involve pretty strong forces. Example :

a string is strong enough to support a 10 kg mass. When will the string break if I use it to rotate a 10 g mass in a circle of radius 1m ? And when the string breaks, in what direction and with what speed will the 10 g mass move ?

Examples of circular motions and corresponding centripetal forces :

1.

car going around a curve on a flat road, the force is provided by tire friction. But we have learnt that friction can produce a force only up to a certain value. If you go too fast around too sharp a curve ......

2.

airplane making a turn : to do that, the plane banks and the lift force (the force that keeps the plane afloat, due to the plane's velocity and the proper wing profile) acquires a component parallel to the ground, and directed towards the center of the bend. But sometimes knowing too much physics is bad for you : whenever I find myself in a banking plane, I can't help thinking that, to turn,the plane is using a portion of the force that keeps it afloat...)

3.

pendulum on a turntable, here the force is given by the tension of the string. Let's work this one out.

4.

car turning on a banked curve : there is a "magic value" of bend radius, velocity and banking angle for which you can go around a bend even on a perfectly frictionless surface. Here the centripetal force is provided by the horizontal component of the normal force, and the final expression relating v,r and $\theta$ is identical to the one we have found for the pendulum.

And what about the centrifugal force ? There ain't no such thing, although in some instance you might believe that there is : when you go around a bend, it might feel like someone is pushing you away from the bend, against the car's side. This is the same "non-force" that we discussed for the case of the car breaking and you hitting your nose on the windshield. What is happening is that, because of inertia you would like to continue with the same magnitude and direction of velocity you were having. Rather than centrifugal force, one should talk about "tangential inertia"....

Uniform Circular Motion and Gravity

We all know that it is gravity which is responsible for keeping planets in orbit around the sun, the moon around the earth, etc.

(in the following, we will assume for simplicity that the orbits are circular. You probably know that in reality they are elliptic, but the ellipses are not very "eccentrical", so the circle is a good approximation).

We also know that the force of gravity is directed along the line joining the two bodies, therefore the condition that the force points towards the center of the circle is satisfied.

Parenthesis : we know that if A exerts a force on B, B exerts a force on A, and in fact we do know that the earth attracts the sun with the same force that the sun attracts the earth. Therefore we should conclude that, if this force is responsible for the earth to orbit around the sun, then also the sun should orbit around the earth, and in fact it does. But given that the mass of the sun is so much larger, the sun's (centripetal) acceleration will be proportionally much much smaller, and can be neglected for all practical purposes.

Can we put together what we know about gravity and centripetal force ? If gravity is what provides the centripetal force to keep the planets in orbit, then one must have, for any given situation,

F_gravity = F_centripetal,

i.e. for the earth-sun case

GM_sM_e/r² = M_ev²/r

and, solving e.g. for v

$v = \sqrt{GM_{s}/r}$

which tells us that velocity and radius are tightly connected, and once one of the two is fixed the other can only have one well defined value. And this is true for any possible situation of an object orbiting around a much more massive body, provided we replace for the mass of the sun the appropriate mass of the attracting body.

We can get another interesting relation if we remember the connection between velocity and period. From v² = GM_s/r and $v=2\pi r/T$, we get

$GM_{s}/r = 4\pi^{2}r^{2}/T^{2}$,

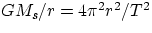
which can be written as

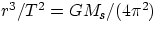$r^{3}/T^{2} = GM_{s}/(4\pi^{2})$ = constant

This is one of Kepler's Laws, obtained empirically from astronomical observations on the orbit of all the known planets. Obviously Newton proceeded in the opposite way : starting from the knowledge of Kepler's laws, he was able to deduce the Law of Universal Gravtitation, obtaining a more complete, physical rather than purely geometrical, interpretation of the phenomenon.

The Moon is falling !!

What would happen to the moon if the hand of God were to suddenly stop it ?

And what would instead happen to it if the same (or any other) hand would suddenly switch off the force of gravity ?

From these two examples we can realize that the actual motion of the moon is due to the combination of the fact that the moon, while being attracted towards the earth, also has a certain non-zero velocity, and a certain amount of inertia (i.e of reluctance to change its velocity). But, in a sense, the moon is, at any instant "falling" towards the earth. Just compare what its position would be if you turn off gravity or leave it on...

Whichever way you want to put it, it is a fact that, at every instant, the moon feels a force attracting it towards the earth, and moves accordingly. The same thing happens to astronauts or any other orbiting object : astronauts and their vessel, at any instant, feel a force directed towards to the earth, and both bodies "fall" in the same way. So this is pretty much the same situation of being in the elevator with the broken cable: both you and the elevator fall at the same rate, responding to the force directed towrds the earth. The only difference is that, in the case of the astronauts, the direction of the attracting force changes continuously, but this does not change the final effect.

As you might have heard, weightlessness is undesireable for extended permanence in space. The solution would be to create artificial gravity. What does that mean? Well, the main eefect of gravity is to cause an acceleration towards the floor, we could get the same effect if we stand in a spaceship, which is rotating at a rate such that the centripetal acceleration is numerically equal to g....

I had promised you that the material of Chapter 5 would be somewhat easier and that, once you understand mv²/r, there is not much more to it. The ease does not apply necessarily to Section 5.7 (Vertical Circular Motion), which is definitely at a higher level of difficulty. This is because we are dealing with a continuously varying situation:

in the Uniform Circular Motion, the magnitude of the force is constant, and so is the magnitude of velocity. The force direction is not constant, but it is well behaved, since it always points towards the center.

When dealing with Vertical Circular Motion, we have a force, the Normal Force, pointing towards the center (therefore rotating around as the body rotates) and the weight force, always pointing downwards. The resultant will not point towards the center, therefore we are in a situation where both magnitude and direction of velocity do change.

The general procedure to attack this situation is the usual one of imposing the condition that the centripetal force (mv²/r) has to be given by the (algebraic) sum of the normal force and the component of the weight directed towards the center