


Next: About this document ...
Lecture 9
Gravitational Potential Energy
Let us investigate what happens when the force doing work is the force
of gravity. Specifically, let us examine a free-falling body, in the following
scenarii :
- 1.
- a body of mass m falls to the ground from a height h. Remembering that work
is given by Force x displacement x cosine of the angle
between the two, in this simplest case we have :
Force = mg, displacement = h,
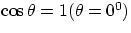
- 2.
- starting from the same height h, the body is tossed up in the air,
it reaches a
certain height, and then eventually it falls down to the ground. We can divide the
motion into three parts, 1) the trajectory from the starting point to the highest
point hmax, 2) the trip back from hmax to the starting point and 3) the
final trip from the starting point to the ground. One can immediately see that the
work done by gravity in 1) is equal and opposite to that done in 2), so that the two
contributions cancel out, and what is left is only the work to cover the original
height h, i.e. W = mgh.
- 3.
- the body is thrown horizontally from the same height h, and eventually it
falls to the ground. We can analyze this situation in the following way : the total
displacement is the combination of a horizontal and a vertical displacement. The
horizontal displacement does not contribute to the work, since the force (gravity)
is perpendicualr to it, so once again we get, for the total work, W = mgh
For simplicity we had assumed that the body was going from a height=h to a height = 0.
In general, we could say that when a body goes from a height hinitial to a height
hfinal, the work done by gravity is
W = mg( hinitial - hfinal)
Moreover, the work depends only on the initial and final positions, and not
on the path followed to go from one to the other.
A force obeying such a property is called a conservative force. For a while,
gravity will be the only conservative force we will deal with (another important one
we will study next year is the electrical force).
Let us examine our falling body further : as it falls from a height h, the body
acquires a certain velocity v, i.e. a certain Kinetic Energy 1/2mv2. Where does this
energy come from? We have seen a while ago that the gain in kinetic energy of a body is
given by the net work being done upon it. In this case the net work is done by gravity,
and it is mgh. We can then write
1/2 mv2 = mgh
which can be interpreted in the following way : at the beginning, the body, thanks to
its "elevated position" has some potential energy (i.e., remembering the
definition of energy, it has the "capability" of doing work). This potential energy
mgh transforms itself into an equivalent amount of kinetic energy as the body
falls to the ground.
Once again we have to be careful with the meaning of "h" : if we say that a body at a
given height h has a gravitational potential energy mgh, we are entitled to ask : with
respect to what should I measure h ? With respect to the ground ? But would the energy
increase if I dig a hole under the object? Or if a body is sitting on a table on the
second floor, should the energy be with respect to the floor of the (second floor) room
or with respect to the ground floor ?
The answer is that, in any given situation, what comes into play is not an absolute
value of potential energy, but the difference in energy between two levels h1 and
h2. Therefore, it doesn't matter what the reference point is : for any given problem
what will matter will be the difference in energy between h1 and h2, and the
difference is always the same, regardless of what I choose as "0 level" (and, as usual,
when doing differences pay attention to the signs).
Having said this, we can generalize the result obtained above : take a body that has
an initial velocity vi and an initial height (measured with respect to an arbitrary
level) hi. When moving under the sole influence of gravity to another level hf
its velocity changes to the value vf. As usual the change in kinetic energy is given
by the work of gravity, i.e. by the change in potential energy. In formulae :
1/2mvf2 - 1/2mvi2 = mghi - mghf, i.e.
1/2mvf2 + mghf = 1/2mvi2 + mghi
(Ekin + Epot)final = (Ekin + Epot)initial
But, in any given situation, we can choose the "initial" and "final" instant to be
whichever ones we want. The above condition is then equivalent to
Ekin + Epot = constant
This represents the Conservation of Mechanical Energy :
when a body moves solely under the influence of the gravitational force, the
sum of its gravitational potential energy and its kinetic energy is constant
Notice that, in general, we should have said " ...under the sole influence of
conservative forces...." and "...its potential energy....", but as I said before, for
a while gravity is the only conservative force we deal with. Remember also that any force
which is perpendicualr to the displacement (e.g. tension or normal force) does not need to
be included in the energy balance equation since it does no work.
The principle of Mechanical Energy Conservation is enormously useful, and it facilitates
the solution of a large class of problems (e.g. : what height will reach an object
thrown vertically ? with what velocity will an object hit the ground and how will this depend
on the actual trajectory? and what velocity will it have at any point in its trajectory? etc.)
So far so good, but what if we need to handle the (more realistic) situation where
non-conservative forces (e.g. friction) are present ? We can almost guess the answer:
- 1.
- Mechanical Energy is not constant anymore, but in fact
- 2.
- the change in total Mechanical Energy is equal to the total work done by the
non-conservative forces, i.e.
and be sure to remember that each one of the three terms in the equation can be either positive
of negative.
Power
In many situations, it is not enough to know how much work is being done, but also
how fast is the work done. If I want to bring a 20 kg load up to the 5th floor (h=15 m), it
does make a difference whether I do it in three minutes walking upstairs, or in 30 seconds
with an elevator; but in either case the work is the same = mgh . We call Power
the rate at which work is being done (or, which is the same, the work done in unit time):
Power = Work/time = W/t
No need to stress that, even if the rate of doing work is not constant, but W is the total work
done, the above expression is still valid, but the quantity W/t represents the average
power. The SI unit for power is joule/sec = watt. A common (historical) unit for power is....
the horsepower. 1 hp = 746 W = 0.746 kW . How much is your "personpower"
You can test it by running upstairs and measuring how long it takes you to gain a certain
height : suppose you climb 10 meters (about 3 flights of stairs) in 10 seconds and your mass is
70 kg: the average power is ..... 80% of a horse. For sustained work, human beings are only
worth 10-20% of a horse.
A unit you have often heard of is the kilowatthour (kWh) : do not be confused, kWh is a measure
not of Power but of Energy (or Work). Here is the definition:
1 KWh is the work done (or the energy consumed) when doing work at the rate of 1 kW for 1 hour.
Therefore :
1 kWh = 1 kW x 3600 sec = 1 kJ/s x 3600 s = 3600 kJ = 3.6 x 106 J
Remembering also that work = force x displacement and that velocity = displacement/time, one
can immediately find the alternative expression :
P = F v
which relates the (average) power involved when a force F acts on an object moving with an
average speed v (notice that, since a net force is involved, speed will vary, so we can only
approach the problem in terms of average speed; in any given problem, do not confuse average
speed with final speed).
Work done by a Variable Force
We know that 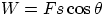 , and we know how to compute it for the case where
, and we know how to compute it for the case where  does
not change along s (or, alternatively, if it is the average value). For this simpler case, if we plot
does
not change along s (or, alternatively, if it is the average value). For this simpler case, if we plot
 vs. s, we get a straight line. Given that W is given by the product of s x
vs. s, we get a straight line. Given that W is given by the product of s x  ,we could say that W is given by the area coverd in the s vs.
,we could say that W is given by the area coverd in the s vs.  plot.
plot.
This result can be generalized to the case of a non-constant Force (varying in magnitude and/or direction).
In this case the s vs.  plot will be an arbitrary curve. But if we divide it in small
intervals
plot will be an arbitrary curve. But if we divide it in small
intervals 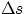 , we could say that, in each interval, the work is well approximated by the product
, we could say that, in each interval, the work is well approximated by the product
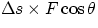 , where
, where  is the value corresponding to each
is the value corresponding to each 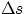 . And the
smaller we make
. And the
smaller we make 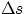 the better is our approximation. The total work will be the sum of all the
small increments, and again will be given by the area covered by the s vs.
the better is our approximation. The total work will be the sum of all the
small increments, and again will be given by the area covered by the s vs.  curve.
curve.
(If you know calculus you will realize that what I am doing is an integral, if you don't, no need to worry,
the idea should be clear enough as presented).



Next: About this document ...
Sergio Conetti
10/11/1999