Chapter 18
Static Electricity
Electricity and the phenomena associated with it are, arguably, the most important features of the physical world as we perceive it. It is safe to say that practically every aspect of the universe around us that we detect with four out of our five senses has its origin in some sort of electrical (or, more precisely, electro-magnetical) phenomenon. Still, as opposed to gravity whose effects were observable since antiquity, electricity effects remained hidden until the 18th century, and this in spite of the fact that electric charges are present in practically every bit of matter surrounding us. Why did electricity remain hidden?
The first lesson we learn is then that electric charges come in two different types (traditionally referred to as positive and negative, but that we could just as well have called black and white, or up and down, or Joe and Mary.....). But, under normal conditions, matter carries an equal amount of positive and negative charges, so that, at a far enough distance from the elementary charges, all electric effects cancel out. But, as soon as we create an even small, imbalance between + and - charges, strong effects are immediately visible.

Nowadays we also know that ordinary matter consists of negatively charged electrons and positively charged protons (plus neutral neutrons that we will ignore for the time being). It is remarkable that, even though electrons and protons are completely different animals, they carry exactly the same (in magnitude) electrical charge. But what do we mean by electrical charge? Probably not even the most brilliant physicist in the world would be able to give you a simple answer. The best we can say is that electric charge is some sort of attribute carried by various elementary particle and, most importantly, electrical charges exert a force upon each other, either repulsive for like charges (++ or - -) or attractive for unlike (+-) charges.
Our knowledge of the nature of electricity at the sub-atomic level allows us to interpret many electrical phenomena in a relatively simple way : when an object becomes negatively charged, this happens because it acquires some surplus electrons, while it is positively charged when it loses a certain number of them.
The standard set of simple elctrostatic experiments shows us that it is reasonably easy to remove or add electrons to various substances, and also that some substances are more likely to lose electrons, while others would rather acquire them.
We could also learn that in some substances (conductors) electrons can easily move throughout the bulk of the substance itself, while for others ( insulators) electrons are hardly mobile at all.
Coulomb's Law
We have said that a force is present between electric charges, and you probably are already familiar with the expression that quantifies the magnitude of such a force: if you have two (point-like) charges 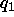and 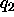separated by a distance r, the electric force between them is (and remember Newton's third law, if 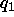exerts a force on 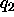, then 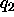will exert an equal and opposite force on 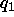) : 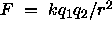where k is a universal constant. In the SI system charges are measured in coulombs and the value of k is 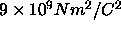. In your textbook the definiton of the coulomb is deferred to a later date. We don't need to do that, since nobody can prevent us from defining the coulomb by using the expression above:
a coulomb is the amount of charge that, when positioned at the distance of one meter from an identical charge, exerts on it the force of 9 x 10 newtons.
From this we can immediately get the feeling that 1 coulomb is a rather large charge. For your information, the charge of the electron (and the proton) is 1.6 x 10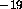 C (or, if you prefer, it takes a little bit less than 10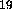 electrons to give you a coulomb worth of charge; this is a large number, but don't forget that one mole of any given substance contains about 6 x 10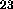 molecules, and each molecule will have several electrons...).

It is apparent that the expression for the electrostatic force resembles Newton's law of gravitation, describing the force between two masses 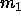and 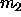. Useful exercise: compare the strength of the electrostatic and gravitational forces acting between the proton and the electron in a Hydrogen atom....
the result is that electric forces are much much more powerful than gravity (in fact gravity is so weak at the sub-atomic level that, as of today, it cannot be investigated experimentally, and it lacks a satisfactory theoretical description). The expression above gives us the magnitude of the electrostaic force between two charges. But remember that force is a vector, and to fully identify it we also need to give a direction. The direction of the force exerted by a charge 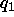on a charge 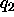will be along the line joining the two charges, and it will point away from 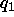if the two charges have the same sign, towards 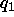if they have opposite sign.
If there are many charges present, the extension is straightforward (at least conceptually ): the net force due to a combination of charges is the vector sum of the forces due to the individual charges.
As examples, we can examine the force exerted on a charge by a pair of two other charges having the same magnitude but either,

• opposite sign (this is called an electric dipole), or
• of the same sign

Question: if you position a charge +q near (but not at) the midpoint between two identical positive charges Q, what will q do?

1. stay still
2. move towards the midpoint, without ever reaching it
3. move to the midpoint and stop there
4. none of the above

Electric Fields
You have probably heard very often people talking about fields, either electric, or magnetic, gravitational, etc., and maybe you have some idea of what is meant by it, but let us introduce the concept properly, starting with a simple case.
Let us start with completely empty space, and then put an arbitrary charge q somewhere in that space. The presence of that charge causes the previously empty space to be modified, in the sense that, in every possible space point, there is now, potentially, a force acting on any other charge positioned there. And, even though, to reveal the presence of q I would need to probe the space with another charge, I could also say that q does something to the space even if I do not do any probing.
We express this by saying that the presence of q gives origin to a Force Field, in this case an electrical force field or simply an electric field. By field then we mean the grand ensemble of all the forces due to the presence of the "field generating" charge. Obviously, as long as I don't go and probe the forces with another charge, these forces remain virtual, since there is nothing they can act upon, but, even so, I can still say that the field of forces is there.....
One definition for a force field I have seen somewhere is : A force field is a region of space under the influence of a physical force We can go on from here and make the field more complicated. I could take two charges, like we have seen before : each of the two separately will generate its own electric field, and the resulting field will be the combination of the two, where by combination we mean the vector sum of the two forces. And, as will be better explained in the following, I could use Coulomb's Law to compute the value of the field (i.e. the value of the force) at any given point. If I add even more charges, the mathematics become more and more complicated, but the idea is the same.
(Parenthesis: I could have made almost identical considerations to introduce the "gravitational field", just replace "charge" with "mass" and "electrical" with "gravitational" in the discussion above)
The definition I just gave you is fine to get an intuitive picture of what is meant by field, but it is not very helpful for any practical purpose. But we will now discuss how to

1. give a graphical representation of a field
2. estimate the strength of a field in any given location

Graphical Representation
As we have seen, the main feature of an electric field is that it originates a (potential) force over the whole extension of space. The standard procedure to represent such a field is to draw a certain number of oriented lines such that, at any point, the direction of the force is given by the tangent to the line. By convention, the direction is chosen to show the force that would be acting on a positive charge. Examples:

• field due to a single charge
• field due to two (either like or unlike) charges
• field of two parallel plates, with uniform distributions of opposite sign charges

A more complicated charge distribution would produce more and more complicated field representations, but if I could manage to draw the field lines (e.g. with the help of a computer), I would succeed in getting a rather good picture of how the field looks like. How many lines should one draw? The choice is somewhat arbitrary, but the convention is to have a number of lines proportional to the strength of the field. Conversely, one could see that the strength of the field in a given region is proportional to the line density in that region (both these statements are best understood by examing the simplest case, i.e. the field of a single charge).
A few rules about field lines (also called lines of force) :

• field lines come out of positive charges and go into negative charges (why?)
• field lines never cross each other (why?)

Field Strength
To probe the strength of an electric field at a point P, we could position an arbitrary charge at P and measure the magnitude of the force felt by the charge. But, ideally, we want to provide a measure of the field strength which is independent of the magnitude of the charge we use to probe it. To achieve this, we define the field strength as the force felt by an arbitrary test charge, divided by the magnitude of the test charge itself, i.e. 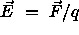where q is the test charge magnitude and F is the force it feels(alternatively we could say that the field strength is the force felt by a unit charge). Field strength is obviously measured in N/C. It is straightforward to obtain an expression for the electric field generated by a single isolated charge Q. If q is our test charge, the field strength at a distance r from the field generating charge will be 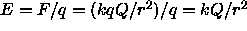More complicated (and more realistic) charge distributions will yield more complicated expressions. We will examine a few interesting cases, but before we do that we need to introduce a new quantity (the electric flux) and a theorem related to it.
Electric Flux
We define as the flux of the electric field through a given surface, or simply electric flux, the net number of field lines that cross the surface in question (note that this definition is different, albeit equivalent, to the one you find in the book. My definition is more intuitive, and gives a better justification to the term "flux"; later on in this chapter's notes I will also present the more rigorous definition of flux ). Using the definition above, it is fairly straightforward to verify, in the simplest cases we have examined, the following rule (Gauss' Law): the net electric flux through any (real or imaginary) closed surface is directly proportional to the net electric charge enclosed within that surface Using our definition of electric flux, and remembering that, when representing an electric field, the number of lines we draw is proportional to the strength of the field, we can verify the validity of Gauss law for the simple cases of 0, 1 or 2 charges:

• draw a closed surface in a field region containing no charges: the number of lines entering the surface will be equal to the number of lines exiting ( a line can only begin or end on a charge), so that the net flux will be zero
• let us now draw a surface surrounding a single charge. All the lines emanating from the charge will cross the surface, and the number of such lines is proportional to the strength of the field, i.e. to the magnitude of the field-generating charge
• let us now consider a dipole (two charges equal in magnitude but of opposite sign). If our surface encloses both charges, again we will have an equal number of entering and exiting lines, and the net flux is zero (and so is the net charge)

For more complicated (and more realistic) situations the law is still valid, but its proof is beyond the scope of this course. As an application, we can obtain the following very important result: any excess charge placed on a conductor resides entirely on its outer surface Here is the reasoning : let's remember that in a conductor, even when uncharged, a certain amount of charges is free to move throughout its body. If we have an uncharged conductor, we can assume that the electric field throughout its body is zero because, if this wasn't the case, then the mobile charges would move around under the effect of the force-field, and the body would not be in electric equilibrium (question: how can we verify that a conductor, when left to itself, reaches equilibrium?)
As a first conclusion, we can then state that in a conductor the mobile charges arrange themselves so as to attain a zero-field configuration throughout its body. Now let us add a certain amount of extra charges (e.g. a bunch of electrons) to our conductor. If we believe that again the object will reach electrical equilibrium, then again we have to conclude that the electric field inside the conductor is zero. But, by Gauss' law, this means that there can be no net charge anywhere inside the body of the conductor, therefore all of the excess charge must migrate to the outer surface.

The absence of electric field inside the body of a conductor, regardless of the amount of extra charge residing on its surface, is equally true when we are dealing with a hollow conductor, and is the basis for electrical shielding. If you fly through a storm, and the plane is repeatedly hit by lightning, you are perfectly safe inside the airplane (even if you touch the airplane's metal body), provided of course that the lightnings do not damage the plane, or that you don't die of a heart attack because of the scare....
Another interesting case is when we put some charge (e.g. positive) inside a hollow, uncharged, conductor (example 18.13). Inside the cavity, the field is the regular one due to the charge q, but inside the conductor,when equilibrium is reached, the field is zero. Gauss law tells us that a closed surface through the body of the conductor must enclose 0 net charge : this can occur since the positive charge q inside the cavity induces an equal charge -q on the inner surface of the conductor (fig. 18.31). Outside the conductor, the field will be as if there is no conductor at all, and only the +q charge was present.
The qualitative definition we have given for the electric flux is sufficient to give us insight into many situations, but, when doing quantitative estimates, we need the following , more rigorous definition: the electric flux through a (real or imaginary) surface of area A is given by 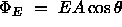where E is the magnitude of the electric field at the surface and is the angle the field makes with the normal to the surface. Obviously this definition can only be applied "as is" if the electric field has a constant value (both in magnitude and direction) all along the surface (two examples in which this is true are given below). In the more general case of non constant field, to calculate the total flux we would need to break up the surface into small sections (possibly infinitesimally small) such that the field is constant over the mini-surface, and, to obtain the total flux, add up all the individual contributions, i.e. Examples of simple flux configurations :

1. spherical surface of radius r centered around a single charge q. At any point on the sphere, the field is perpendicular to the surface and it has the value 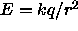, therefore the flux through the sphere is ()
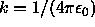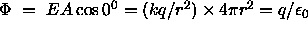
2. parallel plate capacitor, i.e. two parallel conducting plates, one carrying a charge +q, the other -q, uniformly distributed over the plates. By symmetry, one could see that the field has a constant direction, perpendicular to the plates, pointing from positive to negative plate. Application of Gauss law (Example 18.15) shows that inside the gap, the field has a constant magnitude, regardless of the distance from the plates, given by 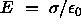where 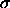is the charge density, .

 
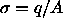• About this document ...