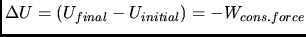Next: About this document ...
Chapter 19
Electric Potential
To start, we should recall some very important facts concerning gravity
and the relation between forces, work and energy:
- massive objects subjected to gravity possess a certain amount of
gravitational potential energy, whose exact value depends on the position of the
object with respect to the source of gravitational force (now we could even say
the source of the gravitational field...). Near the surface of the earth, the potential
energy of a mass m is
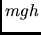 , where h is the height above an arbitrary reference level
, where h is the height above an arbitrary reference level
- given that the choice of reference level is arbitrary, potential energy does
not have an absolute value, we can only talk in terms of potential energy differences between
two different positions
- when acting under the sole influence of gravity, the total mechanical energy of any
object is constant (when a body is in free fall, we witness a continuous transformation of
potential energy into kinetic energy, but their sum remains constant). A more general form
of this statement would be: when under the sole influence of conservative
forces the sum of potential + kinetic energy is a constant.
reminder : a force is conservative when the work it does on a moving object depends only
on the initial and final position, and not on the path followed. Gravity is an obvious
example of a conservative force.
- work done by a force on a moving object is defined as force times
displacement times the cosine of the angle between force and displacement,
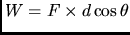 . This implies that in general, when a force acts on a moving object, its work can
be positive, negative or even zero (force perpendicular to displacement).
. This implies that in general, when a force acts on a moving object, its work can
be positive, negative or even zero (force perpendicular to displacement).
- whenever one or more forces do some work on a moving object, the result is some sort of
energy transfer from one form to another. When you have both conservative and non-conservative
forces :
- if the net force is zero, then the end result will be to change the object's potential
energy. Example: lifting a mass m, with constant velocity, from 0 to a height h; the net work
is zero, since the work done by the lifting force is equal and opposite to the work done by
gravity. But, as there is a non-conservative force involved, i.e. the lifting force, then the
(mechanical) energy of the object changes from 0 to
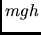 . Notice that this does not violate
energy conservation, since the lifting force must get its energy from somewhere, either your
muscles, or some engine.
. Notice that this does not violate
energy conservation, since the lifting force must get its energy from somewhere, either your
muscles, or some engine.
- if on the other side, some net work is done on the body, the body will also increase
its kinetic energy. Example: a plane climbing with increasing velocity; in this case, the
work done by the engine both overcomes the force of gravity and gives some extra
(kinetic) energy to the plane.
In either case, there is a relation between the work done by the conservative force and the
change in potential energy. Specifically, if U is the potential energy, one has
We have seen that there are similarities between electricity and gravity. It is then logical
to believe that an electric charge, when positioned within an
electric field (i.e. when under the influence of some configuration of net charges)
will possess a certain amount of electric potential energy. How can we be sure of
that? Well, if we have a charge in an electric field and let it free, the charge will move
under the influence of the force-field. But (motion x force) means work; by being in the field,
the charge has the potential of doing work, i.e it has potential energy...
It would be nice to obtain a simple relation for the electric potential energy (something
similar to 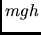 ) but, when dealing with electricity, things are not so simple, for the following
reason:
) but, when dealing with electricity, things are not so simple, for the following
reason:
we should not forget that 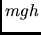 is an approximate expression, that assumes that, as a mass
moves through the earth gravitational field, the strength of gravity remains constant. As we
rememeber, the strength of gravity, on earth, depends on (the inverse square of) the distance
from the center of the earth. As long as our changes in altitude are small with respect to
the earth radius, then we can assume that gravity is constant and apply the approximate
expression
is an approximate expression, that assumes that, as a mass
moves through the earth gravitational field, the strength of gravity remains constant. As we
rememeber, the strength of gravity, on earth, depends on (the inverse square of) the distance
from the center of the earth. As long as our changes in altitude are small with respect to
the earth radius, then we can assume that gravity is constant and apply the approximate
expression 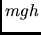 . But, in general, such an approximation will not be possible when dealing with
electricity, since, in most cases, changes in position of the charges under exam will not be
negligible when compared to the distance between charges. Consequently, we will not be allowed to
use an expression that assumes constant force.
Still, we can examine some simple situations:
. But, in general, such an approximation will not be possible when dealing with
electricity, since, in most cases, changes in position of the charges under exam will not be
negligible when compared to the distance between charges. Consequently, we will not be allowed to
use an expression that assumes constant force.
Still, we can examine some simple situations:
- parallel plate capacitor: we have seen that between two parallel conducting plates
charged with equal and opposite charges there is a constant electric field (given by
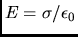 ). But having a constant field means that a charge will feel a
constant force anywhere between the plates, and this is then a situation we can handle.
What will be the difference in electric potential energy for a (negative) charge q when
near the positive plate vs. being near the negative plate? To answer the question we must
estimate the work needed to move the charge from the positive to the negative plate (the
gravitational equivalent would be moving uphill). If d is the plate separation, we have
which then gives the value of the difference in electric potential energy the charge q
has at the negative vs. the positive plate of a capacitor. If I was to release my charge
after having forced it to the negative plate, it would move
from the negative to the positive plate under the effect of a constant force (therefore with
constant acceleration). In doing so, all of its potential energy would
eventually be transformed into kinetic energy.
). But having a constant field means that a charge will feel a
constant force anywhere between the plates, and this is then a situation we can handle.
What will be the difference in electric potential energy for a (negative) charge q when
near the positive plate vs. being near the negative plate? To answer the question we must
estimate the work needed to move the charge from the positive to the negative plate (the
gravitational equivalent would be moving uphill). If d is the plate separation, we have
which then gives the value of the difference in electric potential energy the charge q
has at the negative vs. the positive plate of a capacitor. If I was to release my charge
after having forced it to the negative plate, it would move
from the negative to the positive plate under the effect of a constant force (therefore with
constant acceleration). In doing so, all of its potential energy would
eventually be transformed into kinetic energy.
Example :
a)Let A, q and d be the area, charge and width of a parallel plate capacitor. If an electron
is released with zero initial velocity near the negative plate, what will its velocity be when it
reaches the positive plate?
b)Answer question a) in terms of voltage difference between the plates
c) Answer question a) using eV's
- electric field due to a single positive charge Q. What will be the electric potential energy
of another charge +q, positioned at a
distance r from Q? To find the answer, we first need to choose our zero-energy reference level.
The standard choice is to set the potential energy to zero when the charge separation is infinitely
large. To estimate the potential energy of q at a distance r from Q, I then
need to calculate the work required to move q from infinity to r. But this case is not as
simple as the previous one, since, as q moves towards Q, the electric force is not constant
but it keeps growing. The problem can be solved using calculus, with the answer :
From this, we can also infer that the difference in electric potential energy of a charge q between
two different positions, at respective distances
 and
and 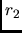 from Q is
from Q is
Electric Potential
In spite of the fact that Electric Potential Energy is an important concept, we are not going to
encounter it too often in the future. Instead, we will mostly deal with a related quantity, the
Electric Potential, also referred to as Electric Voltage.
DO NOT CONFUSE ELECTRIC POTENTIAL ENERGY WITH ELECTRIC POTENTIAL
they are related to each other but they are not the same thing. Here is how it goes:
we have already seen that, when dealing with electricity, it is more useful to think in terms of
electric fields rather than electric forces, and we have defined the field vector as the force
acting on a unit charge (or, which is the same the force acting on a charge divided by the
charge's magnitude).
Similarly, rather than dealing with electric potential energy, we introduce a new quantity, the
electric potential, defined as the (electric) potential energy of a given charge, divided by
the charge magnitude, or, equivalently, the potential energy of a unit charge.
V = EPE/q
As for potential energies, electric potentials are meaningful only in relative terms, i.e. as
differences between two different locations in
an electric field. Based of the definition just given, we can say that the potential
difference between two points is the difference in potential energy that a unit charge would have
in the two locations or, which is the same, it is the work required to move a unit charge
from one point to the other. Electric potentials are measured in volts and from our
definition it follows that
1 volt = 1 joule/1 coulomb
From the results we had obtained earlier we can immediately obtain the expression for the potential
in some simple cases:
- the potential difference between the plates of a plane condenser with charge density
 and plate separation
and plate separation 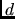 is
But let's not forget that
is
But let's not forget that 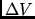 = work to move a unit charge from one plate to the other,
therefore
where E is as usual the magnitude of the electric field inside the capacitor. This result shows that
it would be legitimate to measure field strengths in volts/meter (and in fact this is the more
customary way to express a field strength). But earlier we were measuring fields in newton/coulomb.
Are the two set of units equivalent?
= work to move a unit charge from one plate to the other,
therefore
where E is as usual the magnitude of the electric field inside the capacitor. This result shows that
it would be legitimate to measure field strengths in volts/meter (and in fact this is the more
customary way to express a field strength). But earlier we were measuring fields in newton/coulomb.
Are the two set of units equivalent?
- the potential at a distance r from a point charge Q is
In this last expression one must take into account the sign of the charge: a positive Q charge will
generate a positive potential in
the region surrounding it, while a negative charge will give origin to a negative potential. When
dealing with a single charge we also have that the difference in
potential between two positions  and
and 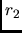 is
If we have more than one charge, the total potential at any location is the (algebraic) sum
of the potentials due to the individual charges. A more rigorous treatment would show
that the most general expression relating field and voltage is
is
If we have more than one charge, the total potential at any location is the (algebraic) sum
of the potentials due to the individual charges. A more rigorous treatment would show
that the most general expression relating field and voltage is
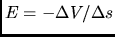 , where the
minus sign accounts for the facts that positive charges move from higher to lower potentials and the
field direction shows the force acting on a positive charge. This expression can be used when dealing
with variable fields, in which case it has to be evaluated over a suitably small
, where the
minus sign accounts for the facts that positive charges move from higher to lower potentials and the
field direction shows the force acting on a positive charge. This expression can be used when dealing
with variable fields, in which case it has to be evaluated over a suitably small 
Conceptual question 19.6: compare electric field and electric potential at the midpoint of two
identical charges, for the cases of same sign or opposite sign.
More on units
If you move one electron in an electric field region from a 0 V location to a -1 V
location, the electron will acquire a (potential) energy of
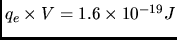 . Similarly, if you let one electron move, under the influence of a field, from
a -1V to a 0 V position, the electron will undergo an energy transformation (from potential to kinetic )
of
. Similarly, if you let one electron move, under the influence of a field, from
a -1V to a 0 V position, the electron will undergo an energy transformation (from potential to kinetic )
of
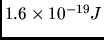 . When dealing with atomic and sub-atomic phenomena, it is then convenient to
introduce a new energy unit, i.e. the electron volt, defined as the energy involved when a charge
equal to the electron charge moves across the potential difference of 1 volt. Be sure to understand that the
electron-volt (and its multiples MeV, GeV, etc.) is just an energy unit like any other (i.e. joules,
calories, Btu's, etc) and one has
. When dealing with atomic and sub-atomic phenomena, it is then convenient to
introduce a new energy unit, i.e. the electron volt, defined as the energy involved when a charge
equal to the electron charge moves across the potential difference of 1 volt. Be sure to understand that the
electron-volt (and its multiples MeV, GeV, etc.) is just an energy unit like any other (i.e. joules,
calories, Btu's, etc) and one has
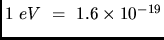
Equipotential surfaces
Let us consider the parallel plate capacitor. We have seen that, between the plates, the electric field
is constant and given by  , where d is the plate separation and V the voltage difference between
plates. What is the voltage at an intermediate location d' ? To answer this, we need to estimate the work
required to move a unit charge to the location d', i.e.
, where d is the plate separation and V the voltage difference between
plates. What is the voltage at an intermediate location d' ? To answer this, we need to estimate the work
required to move a unit charge to the location d', i.e.
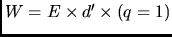 . From this we see that,
within the plate's
spacing, all the points of a plane parallel to the capacitor planes have the same potential V=Ed',
where d' is the plane's position. We call this plane an equipotential surface, and we notice that
it has the following properties:
. From this we see that,
within the plate's
spacing, all the points of a plane parallel to the capacitor planes have the same potential V=Ed',
where d' is the plane's position. We call this plane an equipotential surface, and we notice that
it has the following properties:
- an equipotential surface is perpendicular to the field lines
- no work is done by the electric field when a charge moves along an equipotential surface. Moreover,
no net work is done when a charge follows an arbitrary path that begins and ends on the same equipotential
surface.
(statements 1 and 2 are in fact related, one could show that 1 follows from 2 and viceversa) .
Equipotential surfaces do exist for any possible field configuration, the rule to establish them would be
to draw the lines that at every location are perpendicular to the field lines ( a computer could easily do
that for any arbitrarily complicated field). Apart from the parallel plate capacitor, the next simplest
case is the one of the field generated by a single charge: in this case equipotential surfaces are spheres
centered on the isolated charge.
Another immediate conclusion is that the surface of a conductor, whether charged or uncharged, is
equipotential. If this wasn't the case, free (positive) charges would migrate from regions of higher to
lower potential energy, the same way that a free mass spontaneously falls to the region of lowest
gravitational potential(negative charges would do the opposite, i.e. they would move towards higher
potentials).
Capacitance
From what we have just learned we can conclude that, when we add some extra net charge to a conductor,
upon reaching equilibrium the whole body of the conductor settles at some constant voltage. A legitimate
question would be : what will this voltage be, for a given amount of net charge? This question is
equivalent to asking: if we pour a certain amount of water in a container, what level will the water
reach? The answer obviously depends upon the capacity of the container, i.e. something related
to its size and shape. The same happens with electricity : when adding a certain amount of charge to a
conductor, it settles at a voltage determined by the conductor's capacitance,
i.e something related to its size and shape. We express this idea with the relation
V = Q/C
For a given charge, the larger the capacitance, the lower the voltage level. Conversely, if we bring a
conductor to a fixed voltage, e.g. by connecting it to a battery, the larger the
capacitance the more charge we can store on it.
Typical Problem : a charged and an uncharged conductor of given capacities are brought into contact and
then separated. How will the total charge be distributed among the two conductors? And what will be their
voltage?
(Key to the solution : when brought together, the two conductors become equipotential, and their voltage
does not change after they are taken apart).
Capacitance is measured in farads, whose defintion is obviously:
1 farad = 1 coulomb/1 volt
Application: thinking of the earth as a large conductive sphere, what is its capacitance?
To answer the question we need an expression for the capacity of a sphere of given radius. We can obtain it
by recalling that, when we have a charge q inside a hollow spherical conductor, an equal charge q is induced
on the conductor's outer surface, and the field generated by this charge is identical to the one that would be
generated by the point charge q inside the conductor. We can then also say that the voltage at the sphere's
surface is the same as that produced by a point charge  . Therefore
Applying this to the earth would show that 1 farad corresponds to a rather large capacitance.
. Therefore
Applying this to the earth would show that 1 farad corresponds to a rather large capacitance.
When dealing with capacitance, a very important case is the one we have already encountered a few times,
i.e. the parallel plate capacitor, since this configuration allows to maximize the capacitance
(i.e is capable of storing relatively large amounts of charge). We study the parallel plate configuration
since it is the easiest one to handle, but be aware that, in general, a capacitor is any pair of
conductors separated by an insulator and carrying equal and opposite amounts of charge. From what we have
learnt, we can immediately obtain an expression for the capacitance of a parallel plate configuration, in
terms of its geometry. We have seen that V = Ed, where d is the plate separation, and also
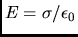 , where
, where  is the charge density, i.e.
is the charge density, i.e.  =q/A (A=area of the plates). We
then have
=q/A (A=area of the plates). We
then have

, therefore
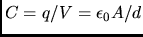
Dielectric constant
Even though we have not stated it explicitely, so far we have assumed that the space bewteen the plates was
empty. The situation changes when an insulating material is inserted between the plates. As discussed in
the textbook, the effect of the insulating material, referred to as dielectric, is to lower the
value of the electric field in the capacitor gap (some of the field lines are "swallowed" by space charges
forming at the edges of the dielectric). The reduction in field strength depends on the prpoerties of the
material (air e.g. has hardly any effect, and is almost equivalent to vacuum) and is expressed in terms of
the material's dielectric constant  , defined as
wher
, defined as
wher 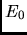 and E are respectively the field without and with dielectric (consequently
and E are respectively the field without and with dielectric (consequently 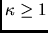 ).
When a dielectric is present, the expression for the parallel plate capacitance then becomes:
showing that the inclusion of a dielectric has the effect of increasing the capacitance(therefore allowing
to store more charge for a given voltage).
).
When a dielectric is present, the expression for the parallel plate capacitance then becomes:
showing that the inclusion of a dielectric has the effect of increasing the capacitance(therefore allowing
to store more charge for a given voltage).
Finally, let us estimate how much energy is stored in a capacitor. If a capacitor is charged up to a voltage
V by an amount of charge q, the work involved is given by
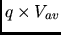 , where
, where 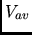 is the average
value of the voltage as the capacitor is being charged. But since the voltage varies linearly with charge,
the average voltage is just the intermediate value between initial and final, i.e.
is the average
value of the voltage as the capacitor is being charged. But since the voltage varies linearly with charge,
the average voltage is just the intermediate value between initial and final, i.e.  . We then
have
. We then
have
Energy =
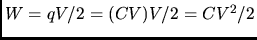



Next: About this document ...
Sergio Conetti
2003-01-29
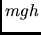 . Notice that this does not violate
energy conservation, since the lifting force must get its energy from somewhere, either your
muscles, or some engine.
. Notice that this does not violate
energy conservation, since the lifting force must get its energy from somewhere, either your
muscles, or some engine.