


Next: About this document ...
Chapter 21
Magnetism
You all know that, apart from the gravitational and the electric fields, another field
exists in Nature, the Magnetic Field. Armed with your understanding of the electric
field, if asked what the magnetic field is, you might guess that it is the concept representing
a certain region of space affected by some sort of magnetic force.
If then asked what could be the source of such force, extrapolating from your knowledge of
the electric field, you might venture that it should be some sort of magnetic charge.
This would be a reasonable assumption, but unluckily, as of today, no one has ever
detected a magnetic charge, even though there are good theoretical grounds to believe that
such an exotic animal, called magnetic monopole, might exist, and some scientists have
been spending their life trying to find one....
But if there is no such thing as a magnetic charge, what is then the source of magnetic fields
and forces ? The answer is relatively simple:
all of our knowledge of magnetism can be
summarized by saying that all magnetic phenomena are associated with THE MOTION of
electric charges. In other words
charges at rest = no magnetism
charges in motion = yes magnetism
The magnetic properties of the ordinary magnets are due to the motion of the magnet's electrons.
Knowing this, you would be entitled to say that all materials have moving electrons, therefore
all materials should exhibit magnetic properties. We will clear this question in
more detail later, but I can anticipate the answer by saying that, in ordinary materials, the
contributions from each electron have random orientation, so that the overall effect is cancelled,
while in magnetic materials the contributions are "aligned", so as to give raise to a
macroscopically observable effect.
The well known fact that magnets come with two different poles (we could say two different
magnetic "charges"), traditionally referred to as North and South and that the
poles cannot be separated is also, as we will better understand later, a consequence of the fact that
the source of magnetism is the motion of electric charges. Finding a magnetic monopole
would mean to find an isolated North or South pole, such an object would have very intriguing
properties....
I will then make the following statements :
electric charges in motion give origin to magnetic forces (i.e. magnetic fields) and, conversely,
an electric charge when moving in a region of magnetic field will feel a certain force
An equivalent statement would be that when electric charges are at rest they only affect each other with
the electrostatic force, i.e. the force described by Coulomb's Law, but, when in motion,
they are subjected to an additional, magnetic, force.
We are then ready to ask ourselves : what is the force felt by a particle of charge q when moving
in a magnetic field (e.g. when between the poles of a horseshoe magnet)? The answer is almost
what you might expect, i.e. the force is proportional to the magnitude of the charge, to the
magnitude of the magnetic field and to the particle's velocity (this should not be surprosing,
we have just said that zero velocity = zero magnetic force). But, when dealing with magnetism,
there is an extra twist: a charged particle moving in a magnetic field will not feel any
magnetic force if its velocity is parallel to the field direction. If B is the magnetic field
strength, We can express all this by
where 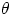 is the angle between the velocity vector and the magnetic field vector (we could
also say that the magnetic force is proportional to the velocity component perpendicular
to the magnetic field. After we know the magnitude, the next
thing we should ask is: what is the direction of the magnetic force felt by our moving charge?
The (certainly not intuitive) answer is the following:
is the angle between the velocity vector and the magnetic field vector (we could
also say that the magnetic force is proportional to the velocity component perpendicular
to the magnetic field. After we know the magnitude, the next
thing we should ask is: what is the direction of the magnetic force felt by our moving charge?
The (certainly not intuitive) answer is the following:
when they are at a non-zero angle, velocity and field vectors define a plane. The direction of
the force is along the perpendicular to such plane (you can get a picture of this with
the help of the right hand rule).
We then see that the magnetic force (and the consequent acceleration) are always perpendicular to the
velocity. Do you recall what type of motion results from such a situation?
(reminder : for an arbitrary relative orientation of velocity and acceleration vectors,
the acceleration component parallel to the velocity is responsible for changing the
velocity's magnitude, while the perpendicular component only changes the velocity's
direction
We can then say the following:
- magnetic forces cause a charged particle to move in a circular trajectory
- magnetic forces do not affect the magnitude of a charged particle velocity
- the work done by magnetic forces on a charged particle is zero
And be aware that this behaviour is different from that due to electric forces : an electric field
acting on a charged particle will always produce a force parallel to the field direction, and,
in the most general case, will change both direction and magnitude of the particle's
velocity (if the velocity happens to be parallel to the field, then only the magnitude will be
affected)
The magnetic deflection of charged particles is exploited in countless applications, ranging from
TV's and CRT's to huge particle accelerators. It is fairly straightforward to obtain an expression
for the radius of curvature of the trajectory of a particle in a magnetic field. Considering for
simplicity the case when the particle's velocity is perpendicular to the field direction
(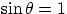 ), the magnetic force is actually providing the centripetal force that keeps the
particle on the circular trajectory, therefore
), the magnetic force is actually providing the centripetal force that keeps the
particle on the circular trajectory, therefore
mv2/r = qvB , r=mv/(qB)
So far we have spoken at length about the magnetic field, but we have not stated specifically how it
is defined and how to measure it. The most straightforward definition can be derived from the
expression for the magnetic force on a charge particle. We will then say that the magnitude of the
magnetic field is given by the force felt by a particle of unit charge moving with unit velocity
perpendicularly to the field, or, in general,
The SI unit for magnetic field is the tesla, T = newton second/(coulomb meter), another common
unit is the gauss 1 T = 10,000 G
Due to its special properties, the definition of the magnetic field is more elaborate than that of the
electric field : electric field was just defined as force per unit charge, while the strength of the
magnetic field has to be normalized not just to the magnitude of the charge feeling the force but also to
its velocity. Moreover, while the electric field has the same direction as the force it
produces, in the magnetic case force and field are perpendicular to each other.
Magnetic forces on electric currents
We have introduced the connection between magnetism and electricity by examining the easier picture
of the field action on a single moving charge. But this is not how the knowledge developed
historically: much before physicists became aware of the existence of electrons and other sub-atomic
particles, they studied in depth the effect of magnetic fields on electric currents. As we
now know that an electric current is the macroscopic manifestation of charge motion, we can certainly
expect that a current-carrying wire immersed in a magnetic field region will feel a force.
The simplest case to analyze is that of a straight wire of length L, making an angle 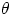 with the
field direction. If q is the amount of charge that crosses the wire in a time t, it will feel a force
or, multiplying and dividing by t
The force direction will be again along the perpendicular to the plane containing the current and
field vectors.
with the
field direction. If q is the amount of charge that crosses the wire in a time t, it will feel a force
or, multiplying and dividing by t
The force direction will be again along the perpendicular to the plane containing the current and
field vectors.
A slightly more complicated, but extremely important case, is that of a current carrying loop
which is free to rotate within a magnetic field. As shown in the book, under the correct arrangement
the coil will be subjected to a torque, given by
where A is the area circumscribed by the loop and 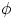 is the angle between the field and the normal
to the surface enclosed by the loop. The effect of the
field can be magnified even further, by wrapping a wire to form several loops, i.e. a coil. Each loop
of the coil will feel the same force, and the overall torque acting on the coil will be
is the angle between the field and the normal
to the surface enclosed by the loop. The effect of the
field can be magnified even further, by wrapping a wire to form several loops, i.e. a coil. Each loop
of the coil will feel the same force, and the overall torque acting on the coil will be 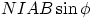 ,
where N is the total number of loops. A current carrying coil in the field of a permanent magnet is the
basic mechanism behind (DC) electric motors.
,
where N is the total number of loops. A current carrying coil in the field of a permanent magnet is the
basic mechanism behind (DC) electric motors.
Pause to recollect thoughts :
- 1.
- you were told that all magnetic phenomena are associated with moving charges
- 2.
- we have seen so far that
- (a)
- magnetic fields exert forces on moving charges
- (b)
- magnetic fields exert forces on currents
- 3.
- but, from 1, we can also expect that
- (a)
- currents generate magnetic fields and, therefore
- (b)
- currents exert forces on currents, and also
- (c)
- currents exert forces on magnets
Magnetic fields generated by currents
We are going to limit ourselves to the study of 3 simple configurations, i.e.
- 1.
- a long straight wire
- 2.
- a current loop
- 3.
- a solenoid, i.e. a long coil of wire wrapped around into a very large number of loops.
For each of these cases, the magnitude of the field will be proportional to the current running through
the circuit. In the case of the wire, there is a simple expression for the magnitude of the field at
any position in space, while for the loop and the solenoid simple expressions are available only for a
limited region in space. So, here are the rules :
- long straight wire : the field lines for the magnetic field generated by a straight wire are
circles concentric with the wire. The line direction is given by the current direction, according to
Right Hand Rule 2 : thumb = current direction, curled fingers point to field direction. At a distance
r from the wire, the field strength is
with
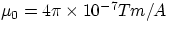 . Knowledge of the field strength can be combined with the
expressions we learnt earlier describing the effect of a field on a moving charge or current, to evaluate
magnitude and directions of magnetic forces generated by a current.
. Knowledge of the field strength can be combined with the
expressions we learnt earlier describing the effect of a field on a moving charge or current, to evaluate
magnitude and directions of magnetic forces generated by a current.
- single current loop : field lines go straight through the center of the loop, while away from the
center they curve to form closed circles. Notice the similarity between the field line configuration due
to a loop and that due to a magnet (also compare with the field shape of an electric dipole): a
current loop behaves like a permament magnet (a more appropriate statement would be that a magnet behaves
the way it does since, inside it, there is a huge number of mini-current loops, e.g. the electron orbits,
all oriented the same way to build up a macroscopic field). The magnitude of the field at the center
of a loop of radius R is given by
If one has a succession of N loops, the field strength is correspondingly multiplied by N.
- solenoid : if one keeps increasing the number of loops, so as to get a fairly long structure, one
is dealing with a solenoid. The main property of the solenoid is that, in its interior, the field
is approximately constant, and directed along the solenoid axis. A "good" solenoid is one for which the
radius is small compared to the total length. When this condition is satisfied, the field inside the
solenoid is given by
where n is the number of loops per unit length
Sections 21.8 : SKIP
Section 21.9 : read and understand



Next: About this document ...
Sergio Conetti
2/15/2001