


Next: About this document ...
Chapter 22
ElectroMagnetic Induction
When dealing with the Electric Field we had introduced the concept of field flux through a
surface, intuitively defined as the number of field lines crossing the
surface or, more rigorously, as  , where A is the area of the surface, E
the magnitude of the field and
, where A is the area of the surface, E
the magnitude of the field and 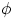 the angle between the field vector and the normal to the
surface. Flux plays an extremely important role when dealing with magnetic fields, so
let us start by re-defining it : the flux of the magnetic field B through an area A is given by
the angle between the field vector and the normal to the
surface. Flux plays an extremely important role when dealing with magnetic fields, so
let us start by re-defining it : the flux of the magnetic field B through an area A is given by

,
where 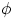 is the angle between the magnetic field vector and the normal to the surface.
It is clear that this simpler definition can only be applied in regions where both the field magnitude
and the relative field/surface orientation are constant. For the more general case, one would need to
divide the surface into small regions of constant field, and, to get the total flux, add up all the
elementary contributions.
is the angle between the magnetic field vector and the normal to the surface.
It is clear that this simpler definition can only be applied in regions where both the field magnitude
and the relative field/surface orientation are constant. For the more general case, one would need to
divide the surface into small regions of constant field, and, to get the total flux, add up all the
elementary contributions.
Now that we know what the flux is, we can introduce a new phenomenon peculiar to the electro-magnetic
realm, i.e. the electro-magnetic induction. To start, let's notice that all the
current+magnetism phenomena we have studied so far were dealing with constant
magnetic fields and constant (=DC) currents, or, in other words, with situations where the
B-flux through any given surface was constant.
When dealing instead with variable fluxes, a new phenomenon appears, described by Faraday's Law:
whenever a conductor enclosing a certain surface experiences a variable flux, a potential
difference is generated between its extremities
moreover
if the conductor is forming a closed circuit, the potential difference (emf) will induce a
current within the circuit
There are many ways to create a flux variation and a consequent induced current :
- the magnitude and orientation of the field generated by a magnet are not constant in space;
moving a wire loop in the vicinity of the magnet (or a magnet in the vicinity of a wire loop) will
induce a current in the loop. An equivalent
effect would be to move a wire loop in the vicinity of an electric circuit carrying a DC current.
- rather than moving things around, I can create a variable magnetic field by sending a variable
current through a circuit. A wire loop in the vicinity of a variable current will experience an
induced current.
- another way to vary the flux is to change the shape of the flux-collecting surface : squeezing
a wire loop (from e.g. a circular to an elliptic shape), once more will cause an induced current
- etc.
Faraday's Law can be expressed quantitatively:
the emf induced in a loop of wire is proportional to the
rate of change of magnetic flux
through the surface enclosed by the wire, i.e.
emf =
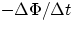
, with
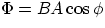
the direction of an induced current is such as to oppose the change in magnetic flux that
originated the itself current
What does this mean ? Let us remember that any current generates its own magnetic field. The
direction of the induced current will be such as to generate a field opposing the change in flux,
i.e. attempting to keep the magnitude of the flux constant. A specific example will help:
let's have a wire loop and a magnet, and move the magnet towards the loop (and let us
suppose that the magnet orientation is such that the field lines point towards the loop).
As we move
the magnet closer, the field becomes stronger, therefore the loop experiences an increase in flux.
The direction of the induced current will be such as to generate a field pointing away from
the loop, i.e. creating a field that should be (vectorially) subtracted from the magnet's field; in
doing so, the loop tries to "cancel" the field increase and to restore the flux to its original
value. If we move the magnet away, the flux decreases and the current will be such as to try to
increase it (again trying to keep things at the original values...)
Motional emf
As a special application of Faraday's Law, we can study what goes under the name of motional
emf. Let us consider a U-shaped conductor, a metal bar sliding along it and a constant magnetic field
perpendicular to the U-plane. As we slide the bar along the U-shape, what is the change in flux?
The flux, in this case is given by BA, where A is the area defined by the bar and the U-wire, and
the change in flux is given by the change in area 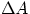 . If the bar velocity is v, the area covered
in a time
. If the bar velocity is v, the area covered
in a time 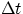 is given by
is given by 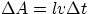 , where l is
the length of the bar. Faraday's Law then tells us (ignoring the sign) :
, where l is
the length of the bar. Faraday's Law then tells us (ignoring the sign) :
emf =
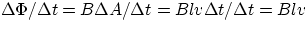
A good way to interpret this phenomenon is in terms of the force exerted by the field on the moving
charges. Here is the reasoning :
as we move the bar in the field region, the magnetic field produces a force on the free electrons
inside the metal bar (remember: a charge moving inside a magnetic field is subject to a force).
What is the direction of the force? It is perpendicular to both the field and the direction of motion,
therefore it is oriented along the length of the bar. This force will cause the free electrons inside
the moving bar to migrate towards one end and, as this happens, a difference of potential is generated
between the extremities of the bar. And here comes an interesting observation: we can obtain the
expression for the emf we have derived before by applying Faraday's Law by requiring that, as
the bar moves in the field region, equilibrium is reached between electric and magnetic
forces acting on the electrons. Specifically :
- magnetic force on the electron : evB
- electric force on the electron : eE = eV/l
requiring the two to be equal gives :
which is the same result we had obtained before using Faraday's Law. We are then led to the conclusion
that at the origin of the induced currents and induced emf is the force felt by charges moving in a
magnetic field.
ElectroMagnetic induction is exploited in countless applications, most importantly the
generation of electric power . The basic principle is quite simple:
if a coil is kept rotating in a region of magnetic field (e.g. between the poles of a magnet) the
flux of the field through the area enclosed by the coil will vary continuously and, as a consequence,
an induced emf (and a current, if dealing with a closed circuit) will be generated.
As an immediate consequence of Lenz's Law we can see that the generated current keeps switching
direction as the coil turns. When the coil's plane is perpendicular to the field lines, the flux is at
a maximum; as the coil rotates, the flux decreases, and the current inside the coil is such as to
create a magnetic field trying to restore the vanishing flux. At the instant when the coil's plane is
parallel to the field lines, the flux is zero, but then it starts growing again. During this phase, the
induced current generates a field opposing the flux growth, therefore the
current direction will be opposite to that of the previous half cycle.
The expression for the induced emf as a function of time for a coil of N
turns is given by (ignoring the - sign)
emf =
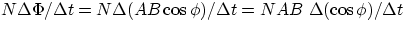
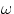 , we have
, we have 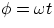 , therefore
, therefore
emf =
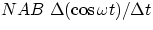
= with some Calculus gobbledygook =
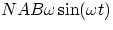
(if you don't know Calculus, don't worry; the important thing to remember is that a uniformly rotating
coil gives raise to sinusoidal emf's and currents; this is not too surprising, especially if you remember
, as you had learnt when dealing with harmonic motion, that the projection of a uniform circular motion
is a sine (or cosine) function, and that what comes into play for the induced emf is the projection of
the coil's surface in the direction of the magnetic field).
Remembering that 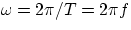 , where T is the period and f its inverse, the
frequency, Alternating Voltages and Currents can be expressed as
, where T is the period and f its inverse, the
frequency, Alternating Voltages and Currents can be expressed as
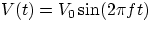
,
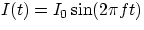
Naively, you might be tempted to write V(t)= I(t)R, but, as we will soon see, when dealing with AC
circuits, life can be much more complicated than this.
Electric Motors and back emf
We have already encountered DC motors, where a coil carrying a DC current (provided e.g. by a battery) is
put into rotation by the torque generated by the field on the current. One can also
have AC motors, where the current in the rotating coil is the Alternating Current supplied by the power
company. For either type of motor we have to deal with a special
effect, again due to electromagnetic induction, that goes under the name of back emf. Here is
what goes on :
as a coil rotates in a magnetic field region, it sees a varying flux and, as usual, it tries to oppose
the change. In other words, as the motor rotates, driven e.g. by the 120 V from the Electric
Company, it produces itself an emf, at all times opposing the one that puts it into motion. As a consequence,
when the motor turns at full speed, it does not see the whole 120 V, but only the difference between 120 V and
the induced emf. But since it takes some time for this back emf to build up within the circuit,
when the motor just starts up it sees the full 120 V voltage and it draws a very large current. This is why
you notice
a dimming of the lights when a heavy appliance kicks on : the (initial) very large current through the
appliance causes a drop in the line voltage (this is similar to what we had encountered when discussing
a battery internal resistance) and all the lights dim.
Another consequence of the back emf (or lack of it)
is the burning out of an electric motor (food mixer, drill, etc.) if for some reason it cannot rotate freely:
if all the voltage is applied to the motor, but the motor is prevented from turning, it will generate no
back emf and the consequent very large current will burn the coil.
Mutual and Self Inductions
you can ignore the discussion and definition of mutual induction, it is enough if you remember
that a coil carrying a variable current will induce an emf and a current in a nearby coil. But
we will discuss the source and meaning of self-inductance
We have seen that when a current goes through a conductor, this gives raise to a magnetic field. Suppose now
that the current going through the conductor is varying with time; the associated magnetic field will also
vary with time, and so will the flux of the field through the area enclosed by the conductor. From Faraday's
Law it follows that the flux variation will generate an emf within the conductor, i.e. the conductor will
self-induce an emf opposing the one producing the variable current. Here is how this effect can be
described quantitatively for the case of a solenoid:
let us start with a solenoid carrying a constant current I; what is the magnitude of the flux through the
solenoid of the magnetic field generated by I ? If 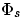 is the flux through a single loop, we will have
is the flux through a single loop, we will have
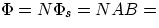
remembering the expression for B inside a solenoid and given that N = nl (l = solenoid length)
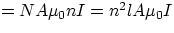
The quantity  , telling us effectively how much self-induced flux we get for a given
current, depends only on the geometry of the solenoid and is given the name of (self-)Inductance L:
Knowing the inductance of a solenoid (or any other component of a circuit) is very useful in determining
the value of induced emf for a given change in current. We have in fact
, telling us effectively how much self-induced flux we get for a given
current, depends only on the geometry of the solenoid and is given the name of (self-)Inductance L:
Knowing the inductance of a solenoid (or any other component of a circuit) is very useful in determining
the value of induced emf for a given change in current. We have in fact
emf =
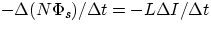
Inductances are measured in henries and from the expression above we see that 1 H = 1V s/A.
A current carrying inductor can be thought of as a storage of electric energy (which is stored in the form
of magnetic field energy). This energy comes from the work one needs to do to reach a certain current I in
the inductor : as the current grows from 0 to I, the inductor emf opposes this growth, and work needs to be
done to overcome this opposition. This work is not wasted, but it ends up as the energy of the magnetic
field created by the current I... One could see that the energy stored in an inductance L
carrying a current I is given by E = LI2/2
Transformers
Another extremely widespread application of electromagnetic induction is the transformer. The basic
idea is fairly simple : a coil (called the primary) carrying an Alternating Current is wound with
Np
turns around an iron core. Another coil, called the secondary and attached to a separate circuit,
is wound with Ns turns around the same core. The effect of the core is to concentrate within itself most
of the magnetic field lines so that, to a good approximation, the same flux of field goes through both coils.
If 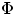 is the flux through a single loop, in the primary there will be a self-induced emf given by
is the flux through a single loop, in the primary there will be a self-induced emf given by
emf
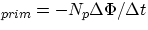
emf
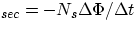
Vs/Vp = Ns/Np
showing how a suitable choice of the relative number of turns in the primary and secondary allows to step up
or down an Alternating Voltage.
In a transformer, electric energy carried by the primary circuit is
transferred (apart from some inevitable losses) to the secondary circuit. The condition of energy
conservation is expressed by
VpIp = VsIs
Question : transformers are routinely used to step up the voltage from power generating plants, so that
electric power transmission over long distances is performed at high voltages (and the voltage is then
stepped down before being utilized by households). What is the advantage of high voltage transmission?



Next: About this document ...
Sergio Conetti
2/22/2001
![]() . If the bar velocity is v, the area covered
in a time
. If the bar velocity is v, the area covered
in a time ![]() is given by
is given by ![]() , where l is
the length of the bar. Faraday's Law then tells us (ignoring the sign) :
, where l is
the length of the bar. Faraday's Law then tells us (ignoring the sign) :
![]() is the flux through a single loop, we will have
is the flux through a single loop, we will have