


Next: About this document ...
Chapter 24
Electromagnetic Waves
By the middle of 1800, a lot of information, both theoretical and experimental, had been gathered about the
properties of Electricity and Magnetism, and the close relation between the two. This body of knowledge was
synthetized in a set of concise and elegant equations by James Clerk Maxwell, showing how Electricity and
Magnetism are just two different manifestations of a unique underlying principle of Nature. Maxwell's
equations (you might have seen them displayed on some T-shirt worn by Physics Majors), achieving the
unification of Electricity and Magnetism are considered among the greatest accomplishments in the
history of Physics, at par e.g. with Newton's Unification of Gravity that showed how the falling of
bodies on earth and the motion of planets and comets are just two aspect of the same underlying phenomenon.
As it often happens in the history of science, a new great theory proves its worth not just in
providing a better explanation for known phenomena, but in predicting the existence and the properties of yet
unobserved ones. In the case of Maxwell equations, an extremely far-reaching prediction was the existence of
ElectroMagnetic Waves. What are they ?
When we first encountered waves, we defined them as some sort of disturbance propagating through a medium:
in water waves water molecules go up and down, in sound waves (in air) air molecules oscillate back and forth,
etc.
In the case of EM-waves, there is no oscillation of any medium : what vibrates, either in vacuum or
within a material, is the magnitude of the electric and magnetic fields. Here is one way to look at
it : if we have a charge at some location in space, it generates an electric field (i.e. it produces a
potential force on any other charge at arbitrary distance from it). Suppose we move our charge back and forth
(or up and down). As a consequence, the value of the field at any point in space will be altered. Moreover,
as we are now dealing with moving charges, we can expect that some sort of magnetic field will also appear.
The question is : how will such effects be transmitted and be felt at some distance from the moving
charge ? The answer that can be deduced from Maxwell's equations is that this disturbance will travel in
the form of a wave propagating through space. More specifically, the wave is a transversal one, with
the electric and magnetic fields always oscillating in planes perpendicular to each
other, both being perpendicular to the direction of wave propagation. If we only move our charge back and
forth once, then we only have a single pulse propagating through space, but if we keep our charges in periodic
motion (e.g. as in the case of an Alternating Current) this will give raise to a continuous sine-like
oscillation of the electric and magnetic fields propagating through space.
But this is not the end: Maxwell's equations provided an expression for the velocity
at which such a disturbance propagates through space. The theoretical result was (in vacuum)
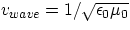
where 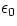 and
and 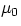 are the usual constants appearing in the expression for electric and
magnetic fields. When the known values for such constants were plugged into the equation, a big surprise
came up : the numerical value found for the wave velocity was identical (within the limits of experimental
error) to the known value for the speed of light !! This led to the conclusion that light (which was
known to be some sort of wave phenomenon of known wavelength) is just some special member of a much larger
family of electro-magnetic waves. The frequencies typical of light waves, as we will see in a moment, cannot
be reached by shaking an electric charge with any available technique. But the type of waves that can be
generated by moving electrons back and forth are the ones that eventually were exploited as radio waves.
Unfortunately Maxwell wasn't there to see his predictions being confirmed: he died in 1879 at the (relatively) young age
of 48, while the first experimental generation of electromagnetic waves was due to Heinrich Hertz in 1887.
are the usual constants appearing in the expression for electric and
magnetic fields. When the known values for such constants were plugged into the equation, a big surprise
came up : the numerical value found for the wave velocity was identical (within the limits of experimental
error) to the known value for the speed of light !! This led to the conclusion that light (which was
known to be some sort of wave phenomenon of known wavelength) is just some special member of a much larger
family of electro-magnetic waves. The frequencies typical of light waves, as we will see in a moment, cannot
be reached by shaking an electric charge with any available technique. But the type of waves that can be
generated by moving electrons back and forth are the ones that eventually were exploited as radio waves.
Unfortunately Maxwell wasn't there to see his predictions being confirmed: he died in 1879 at the (relatively) young age
of 48, while the first experimental generation of electromagnetic waves was due to Heinrich Hertz in 1887.
To get a good insight in the whole spectrum of electromagnetic waves it is essential to remember the general
expression relating wavelength, frequency and velocity of a traveling wave
When dealing with EM-waves, the value of v is the velocity of light c = 3 x 108 m/s. We can
immediately see that a 60 Hz Alternating Current will generate veeery long waves (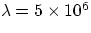 m).
Such waves are neither easily detectable nor very useful. To enter a useful range, we need frequencies of at
least a few hundred kHz (radio "long" waves,
m).
Such waves are neither easily detectable nor very useful. To enter a useful range, we need frequencies of at
least a few hundred kHz (radio "long" waves, 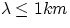 ), followed by radio "medium" and "short"
waves, then the VHF (Very High Frequency) and UHF (Ultra High Frequency) typical of TV broadcast, followed
by microwaves (used for cooking as well as for RADAR apparatus), infrared, visible (
), followed by radio "medium" and "short"
waves, then the VHF (Very High Frequency) and UHF (Ultra High Frequency) typical of TV broadcast, followed
by microwaves (used for cooking as well as for RADAR apparatus), infrared, visible (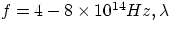 in the few-hundred nanometer range). Then one has Ultraviolet, X-rays and
in the few-hundred nanometer range). Then one has Ultraviolet, X-rays and 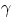 rays.
rays.
Electronic circuitry is capable of shaking electrons back and forth up to frequencies in the microwave range.
Higher frequencies (which, as we will eventually learn, also correspond to higher energies) involve thermal
agitation of matter molecules (infrared), "quantum" jumps of orbital electrons in atoms (visible range),and
high voltage electron
acceleration and deceleration as well as higher energy atomic electron transitions (UV and X-rays).
Finally, "orbital jumps" of protons and neutrons within the nucleus, as well as reactions in high energy
accelerators or in stars are associated with 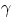 rays. The highest frequency radiation ever observed
comes from
rays. The highest frequency radiation ever observed
comes from 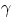 -rays of yet unknown origin in the cosmic radiation, with frequencies in the 1027 Hz
range !!!
-rays of yet unknown origin in the cosmic radiation, with frequencies in the 1027 Hz
range !!!
Energy of EM-waves
EM-waves, like any other wave, do transmit energy from the wave source to its surroundings, in the form of
both electrical and magnetic energy. Another consequence of Maxwell's equation is that EM-waves
carry equal amounts of magnetic and electric energy. A measure of the energy carried from a wave is given by the
energy density, i.e. the energy contained in a unit volume (or, which is the same the energy in a given
volume divided by the volume). One could see that (in vacuum) energy densities are given by
Electric Energy Density =

Magnetic Energy Density =
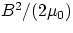
Total Energy Density =

Another commonly used measure of the energy carried by a wave is the Intensity, defined as the amount
of energy crossing a unit area in unit time (= power/unit area). Knowing that the wave is moving with velocity
c, one can relate energy density u to the intensity S :
S = energy/(area x t)
u = energy/volume = energy/(area x ct) = S/c, therefore
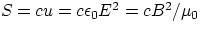
EM-waves (and therefore light) are transverse waves, meaning that the oscillations (of the E and B fields)
occur in a direction perpendicular to the wave direction of propagation. But this condition only identifies
a plane within which the oscillation has to take place, still leaving an infinite number of possibilities for the
actual direction of the oscillation. EM-waves generated by a randomly emitting source (e.g. the light from a light
bulb or from the sun) will have oscillations in all possible orientations perpendicualr to the direction of the
wave: in such an instance the wave is said to be unpolarized. But under special circumstances waves can
be emitted so that the oscillation occur only in a well defined direction (this is what happens e.g. with the
radio emissions from a thin antenna), and the wave is said to be polarized.
When dealing with light, there are special substances ("polarizers") that can transmit only wave oscillations in a
well defined direction, called the transmission axis. When unpolarized light is sent through a sample of
such a substance, it will exit fully polarized. But to interpret correctly the behaviour of a sequence of polarizers,
one should be aware that a given polarizer, for every possible directions of oscillation, will transmit only the
component of the wave parallel to its own transmission axis. More quantitatively, if some portion of a wave is
vibrating at an angle 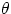 with respect to the transmission axis, only the fraction
with respect to the transmission axis, only the fraction 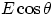 will be
transmitted.
will be
transmitted.
In terms of intensity S, given that 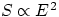 , then
, then 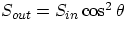 .Keeping this in mind, the following phenomena can be explained:
.Keeping this in mind, the following phenomena can be explained:
- when crossing a single polarizer, the intensity of unpolarized light is halved (the outgoing
intensity is proportional to
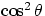 , whose average value is 1/2...
, whose average value is 1/2...
- sending unpolarized light through the succession of two polarizers oriented at 900 with respect to
each other will absorb all the light
- if an extra polarizers, at some angle
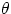 is inserted between two polarizers oriented at 900, some
of the light will reappear.
is inserted between two polarizers oriented at 900, some
of the light will reappear.
To the naked human eye, polarized light is indistinguishable from unpolarized light, but there is some evidence
that some insects and birds can detect the difference. This can play an important role, since indirect light from the
sun can be polarized either by reflection from a surface or from scattering off the air molecules.



Next: About this document ...
Sergio Conetti
3/6/2001
![]() , then
, then ![]() .Keeping this in mind, the following phenomena can be explained:
.Keeping this in mind, the following phenomena can be explained: