


Next: About this document ...
Chapter 25
Light Reflection and Mirrors
We have just learnt that light is an (electro-magnetic) wave, but the wave nature of light was not revealed until
the early 1800 ( as we will learn in some future lecture). Until then, the debate was whether light is some sort
of wave or instead it consists of material particles bouncing around after being emitted from a light source.
Newton himself was a proponent of the particle theory, and obviously he had good reasons to believe that: as we will
see in the next three lectures, most of the observable light behaviour can be interpreted in terms of light
rays, which in turn can be thought of as being due to some material particle emitted by the light source.
If we start examining the most basic properties of light, our first observation would probably be that
light is reflected, and this in in fact why we can "see" light (asking the question "can one see light?" is not as
silly as it might sound).
If we now think of light consisting of a bunch of rays traveling in all directions, by a set of controlled experiments
we could arrive at the main law governing the reflection of light:
the angle at which a light ray is reflected from a surface is equal and opposite to the angle at which the ray hits
the surface, both angles being measured with respect to the normal to the surface
This law is true whether we are dealing with what we normally call a reflecting surface (e.g.
a mirror) or any other surface.
The difference between mirror-like and regular surfaces is that the surface of a
mirror is extremely smooth and uniform, so that a bunch of rays hitting it will retain their relative
orientation after reflection. In ordinary surfaces instead, the direction of a reflected ray is practically
unpredictable, since the surface irregularities do not allow to define a precise direction for the normal to the
surface. Having clarified this, from now on we will just deal with smooth, specular, perfectly reflecting surfaces.
Using the technique of ray tracing together with the law of reflection, we can explain the main
features of plane mirrors :
- if you stand in front of a mirror you see a picture of yourself, while if you stand to the right (left) of it
you will see objects at your left (right)
- the image of an object positioned at some distance in front of a mirror will appear to be on the other side
of the mirror's plane, but at the same distance from it.
An image like this one, that appears to be "inside" the mirror, is called a virtual image to distinguish it
from real images. You might be entitled to ask: what is the difference, aren't all images "unreal", or at
least non-material? Well yes, but here is the difference (you can use this definition in conjuction with the one found
in the book):
we call an image real when it is formed in real, physical space, while it is virtual when it is formed
"behind the mirror", that is in virtual, unphysical space.
Plane mirrors can only have virtual images, to get a real image one needs curved mirrors.
Another intriguing question might be : why do mirrors invert left and right but not up and down ? (or do they? can you
think of a situation where a mirror inverts up and down but not left and right?) For a complete answer, read the
excellent book "The New Ambidextrous Universe" by Martin Gardner.
Parabolic and Spherical Mirrors
For completness, I remind you that a parabola is a curve such that all of its points are equidistant from a fixed point
(the focus) and a line (the directrix). A parabola can be described by the equation y2=2fx, where
f is the coordinate of the focus. You don't need to remember this. but what you do need to remember is a special property
of any parabola :
take a point along the parabola and draw the normal to the curve at that point. Now draw a line from the focus
to this point, and next draw a line making the same angle with the normal, but on the other side: the
geometry of the parabola is such that this last line will always be parallel to the parabola's axis, no
matter where you chose your point.
From this, and from the law of reflection we can infer that :
- in a parabolic mirror, light rays emitted from an object positioned at the focus, will all be reflected in a direction
parallel to the parabola's axis
- conversely, light rays parallel to the parabola's axis will all be reflected towards the focal point.
This property is exploited in your car's headlights, your TV satellite dish, etc.
Parabolic mirrors offer the best "focussing" properties, but they are not easy to build. In most applications, instead
of parabolic mirrors one can use spherical mirrors since in a spherical mirror light rays almost
have the same property of focus convergency, as long as they are not very far from the mirror's axis. This statement
raises two questions:
- 1.
- where is the focal point for a spherical mirror?
Answer : on the mirror's axis, halfway between the mirror's center
of curvature and its surface. In other words, if f is the focal distance. i.e. the distance of the focus from
the mirror's surface, as measured along the mirror's axis, and r the radius, one has f = r/2.
- 2.
- What does "not very
far" mean or, in other words, under what conditions can we say that a spherical mirror behaves like a parabolic one ?
Answer: a spherical mirror will have good focussing properties as long as the distance of the light ray from the
mirror's axis is small when compared to the mirror's radius of curvature (to remind you, an almost flat mirror will have a
very large radius of curvature, while the radius is small for a very "curved" mirror. Which in turns means that the
useful size of a spherical mirror will depend upon its "curviness" : the less curved it is, the larger it can be with
good focussing properties).
Having clarified this, we can state three properties of a spherical mirror, that we will exploit again and again to
understand its behaviour under different circumstances :
- 1.
- any light ray going through the focal point will be reflected parallel to the mirror's axis
- 2.
- conversely, any ray parallel to the axis will be reflected to go through the focal point
- 3.
- a ray going through the center of the sphere will be reflected upon itself. Reason : any line going from the center
to the sphere surface is a radius; radii are always perpendicular to the surface, therefore a radial ray has an incidence
angle of zero and will be reflected upon itself.
Based on this knowledge, we can determine the response of a spherical mirror to objects positioned at different locations.
The cases one distinguishes are: (note : I don't expect you to memorize all this; but you should practice with ray tracing
in order to be able to reach the conclusions presented here for each of the possible configurations)
- 1.
- the image of an object positioned between the focal point and the mirror is virtual, upright and enlarged
- 2.
- the image of an object positioned between the focal point and the center of curvature is real, inverted and
enlarged
- 3.
- the image of an object positioned at a distance larger than the radius is real, inverted and
reduced in size
Convex Mirrors
So far, we have implicitely assumed that we were dealing with concave mirrors, i.e. we were looking at the
"inside surface" of a spherical mirror. But in many applications convex mirrors, i.e. mirrors presenting the
"outside" of the sphere to the viewer can also be useful (aid to memory: to remember what is concave
and what is convex, you can think that a concave surface is associated with a cavity).
When dealing with a convex mirror, we have to be aware that the focus (and the center of curvature) are
"inside" it. We express this condition by giving a negative value to the focal distance. But we can still apply
our ray tracing techniques to determine the behaviour of a convex mirror, with the result:
the image produced by a convex mirror will always be virtual, upright and diminished in size, regardless of the
object's position. Convex mirrors are found e.g. as store security mirrors or car side-view mirrors.
Apart from ray tracing, one can deduce all the results we have found so far by analytical rather than graphical means.
In the same approximation we have adopted so far, i.e. of rays not too distant from the mirror's axis, one could see that
the following formula, called the mirror equation is always valid
1/do + 1/di = 1/f
where do and di are respectively the distance of the object and the image from the mirror's surface. But, to
interpret correctly this equation, it is essential to remember that
- f is positive for a concave mirror, negative for a convex one
- positive di means a real image, negative di a virtual one
- when dealing with combinations of mirrors, one can have "virtual objects", in which case do will be
negative. How can an object be virtual? This can happen since the "object" of the second mirror can be the
image produced by the first and, in some configuration, the first mirror can produce its image "inside" (i.e. "behind")
the second one.
The mirror equation allows us to determine the relative positions of object and image, but does not tell us anything about
size and orientation of the image. But, under the same approximations, one could also derive the magnification
equation: if we define magnification m as the ratio between image size and object size, one could show that
m = -di/do
Here the sign convention is that a positive magnification corresponds to an upright image, a negative to an inverted one.
And, obviously m<1 will mean the the image is smaller than the object, while m>1 corresponds to real magnification.
It is a very useful exercise to verify that these two equations give results consistent with the ones found from ray
tracing for all the different configurations we have discussed before. Equally useful is to see what the equations yield
for the case of a plane mirror (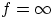 ).
).



Next: About this document ...
Sergio Conetti
3/20/2001