next up previous
Next: About this document ...

Chapter 26

Light Refraction and Lenses

We have seen what light does when it bounces off a surface. But, when dealing with a transparent medium, only a fraction of the light is reflected off the surface, while the remaining fraction penetrates the surface and propagates within the medium. When doing so, two things happen to a light beam:
1.
it slows down
2.
it changes direction
Both of these behaviours are controlled by the properties of the medium, and are characterized by the index of refraction.

Let's discuss the change in velocity first. To start, you would be entitled to ask : "we were told that light always moves at the speed of light, how can it then slow down ?" The answer is that, when propagating through a medium, light, as it interacts with the atoms of the medium, is continuously absorbed and then re-emitted, and it is this process that "slows it down". And the amount of slow-down is determined by the medium's index of refraction n, defined as
n = c/v
where c is the undisturbed speed of light (i.e. the speed in vacuum) and v is its speed in the medium under exam. From the definition it follows that 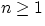$n\geq 1$. The value of n for air is so close to 1 that, for most discussions and practical applications, when light travels through air it is as if it did travel through vacuum.

Indices of refraction are very nearly 1 for most gases (although their actual value does depend upon the gas' pressure), around 1.3-1.5 for many liquids and solids (glasses, crystals, etc.). Diamond dominates the range of refraction indices, with a value as large as 2.4 (therefore light crosses a diamond at only 40% of the speed it would have in air).

What about the change of direction? It is given by Snell's Law
when a light ray crosses the interface between two media of respective refraction indices n1 and n2, the incoming and outgoing directions are related by

$n_{1}\sin\theta_{1} = n_{2}\sin\theta_{2} $
NB : remember, angles are always given with respect to the perpendicular to the surface encountered by the light ray.

Considering the simpler case when one of the two media has an n of 1 (e.g the light is traveling from air to a medium of index n), Snell's law reduces to:
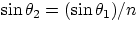
$\sin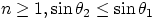\theta_{2} = (\sin\theta_{1})/n $
Since $n\geq 1, \sin\theta_{2}\leq \sin\theta_{1}$, the refracted ray makes a smaller angle with the normal than the incident ray. Conversely, if the ray is moving away from the medium
$\sin\theta_{2} = n\sin\theta_{1} $
and the ray moves away from the perpendicular.

In the more general case,when transiting from a medium of index n1 to one of index n2, the full expression for Snell's Law, $n_{1}\sin\theta_{1} = n_{2}\sin\theta_{2} $, must be applied, but the behaviour will be the same:

rays moving from a medium of smaller to one of larger n will be deflected towards the normal, rays moving from larger to smaller n are deflected away from it.

Because of refraction, a partially submerged straight object appears to have a kink at the air/water interface, and fully submerged objects are not where they appear to be: a spear fisherman must learn to correct the information coming from his eye/brain to correctly aim at a fish....

Finally, if light rays cross some thickness of a transparent material but end up in the medium where they started from (e.g. light going from air through a glass pane and back into air) sequential application of Snell's Law to the two interfaces would show that the rays emerge parallel to the original direction, but shifted laterally.

Derivation of Snell's Law (pages 788-789): skip

Total Internal Reflection

Let's look again the expression we had obtained before, giving the exit angle into air when coming from a medium of index n (e.g. going from water into air) :

$\sin\theta_{2} = n\sin\theta_{1} $
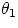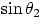It is clear that there must be some situation where this expression cannot be valid: specifically, if the values of $\theta_1$ and n are such that their product is larger than one, this would lead to an impossibility, since $\sin\theta_2$ can at the very most be as large as one. And Mother Nature shows that she has learnt Trigonometry since, under such conditions, no light is allowed to cross the boundary (i.e. there is no refracted light), but all the light is reflected back inside the medium : this is the phenomenon of total internal reflection. 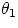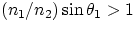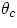More in general, when light encounters the interface between two media of indices n1 and n2 (with n1>n2), light cannot cross the interface if it is incident at an angle $\theta_1$ such that $(n_{1}/n_{2})\sin\theta_{1} \gt 1$, showing that the largest possible angle for which light can escape (called the critical angle $\theta_c$) is given by
$(n_{1}/n_{2})\sin\theta_{c} = 1, \longrightarrow \sin\theta_{c} = n_{2}/n_{1} $
Total internal reflection has been known for a long time,and extensively exploited in devices like periscopes and binoculars, that turn the direction of light by means of prisms. Only recently there has been an explosion of new applications, exploiting a newly developed device, the optical fiber (or fiber-optic). Optical fibers consist of long, thin, flexible filaments of some transparent material(typically glass or plastic) with a large n, coated with a material of smaller n. Thanks to total internal reflection, light entering the fiber at one end will remain "trapped" inside, and will be transmitted with high efficiency to the other end. Fiber optics have already found a wealth of applications,ranging from telecommunicatons to medical diagnosis and surgery.

Polarization of reflected light : we will not discuss this to any depth, it is enough if you reamin aware of the fact that reflection has the effect of polarizing incoming, unpolarized light and, under the right conditions of incidence, reflected light can be 100% polarized.

Dispersion of Light

When we introduced the index of refraction, we stated that each type of transparent material has its own well defined value of n. In reality, things are slightly more complicated, since the value of n depends not only on the type of material, but also on the wavelength of the incident light. For visible light wavelength is related to colour, therefore we can infer that, upon refraction, different colours of light will be deflected by different amounts. Under the right conditions, it is then possible to split light consisting of the superposition of many different colours ('white" light) into its separate components. But notice that the variation of n with 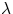$\lambda$ is very small, and consequently the angular separation of different colours (called dispersion) is equally very small; but even a small angular separation can lead to a large spatial separation if allowed to travel a long enough distance...
Example : a ray of white light hits a water surface at a 450 angle. If nred = 1.330 and nblue=1.336, at what angle will red and blue light be refracted? And what will be the separation of the two colours after a 100 m path?
Lenses
Lenses are even more widespread than mirrors in all sorts of optical applications. As we will see, there are several similarities between the behaviour of mirrors and of lenses; on the other side, the behaviour of a light ray in crossing a lens is more complicated than the reflection from a mirror: in the case of lenses one has to apply Snell's Law, involving relations between sines of angles and indices of refraction rather than just the very simple law of reflection. Consequently, we will not try to derive the expressions describing the behaviour of a lens, but will just arrrive at some result in a semi-intuitive way. To start, let's consider what happens to parallel light rays (traveling in a medium with n=1) when they encounter a glass sphere:

upon entering the sphere, application of the law of refraction would show (you should try doing the geometrical construction yourself) that all the rays are bent towards the axis of the sphere, or, in other words, all the rays are made to converge . Moreover, the closer is the ray to the axis of the spherical surface, the lesser is its deflection (in the extreme case a ray traveling along the axis is not deflected at all, since its angle of incidence is zero). And convergence would occur also upon exiting the glass globe : in this case rays are moving from a region of larger to one of smaller n, but the effect of being deflected away from the normal again causes convergence. If we now replace our glass sphere with just two sections of a sphere glued back to back, the response will be the same as that of the full sphere, and we end up with a converging lens.

A proper mathematical derivation would show that, as long as our lens is quite thin, and as long as the rays are not very far from the lens' axis (this is the same condition we had for the spherical mirrors) parallel rays crossing the lens all converge at a unique point, which again we will call the lens' focus; the distance from the focus to the lens is the focal length. At which point you can ask: the distance to which part of the lens, its left face, its right face or the center? To be precise, we should be aware that a lens has two foci, one on each side, and the correct distance would be from the focus to the lens surface (like in the mirror). But remember that we are dealing with thin lenses, therefore we will not be very wrong by referring the focal distance to the lens' midpoint.

Going through the same considerations for a lens consisting of two concave spherical surfaces glued back to back, we would see that incoming parallel rays crossing the lens are all made to diverge, and the divergence is such that their extensions meet at a unique point upstream, of this diverging lens.

We can guess that, in order to study the image forming properties of converging and diverging lenses, we can follow ray-tracing techniques similar to what we had done for the mirrors. From what we have just seen we can immediately state that

1.
a ray parallel to the lens axis will be deflected to pass through the focus
2.
a ray through the focus will become parallel to the axis
In principle, two rays are enough to define a common crossing point, but it is useful to verify our results with a third ray. When dealing with spherical mirrors, we had seen that a ray from the sphere center would be undeflected. With lenses, the situation is different: in this case, the undeflected ray is the one going through the center of the lens. Why is that? We had seen that a ray refracted twice through a slab with parallel surfaces maintains its direction. In the case of the lens, the two faces are, to a very good approximation, parallel at the lens'center, therefore we can conclude that rays through the center will maintain their direction. And, as we are dealing with a thin lens, we can neglect the lateral shift that the ray would undergo in crossing the slab...

If we now try our hand at ray tracing, to examine all the various situations equivalent to those we had studied for the mirrors, the results would be :
1.
Converging lenses :
2.
Diverging lenses :
Notice the complete correspondance between lenses and mirrors. And the correspondance is even stronger, since (thin) lenses obey equations identical to the ones we had found for mirrors, i.e.
1/do + 1/di = 1/f

m = -di/do
But, before we can use these equations, we need to clarify a few items : Focal distance and focussing power
Let us compare two converging lenses of different focal lengths (the arguments could be made identically for diverging lenses, but the reasoning is somewhat more direct for the converging case). Remembering the meaning of focal length, we could say that the lens with the smaller value of focal length has the bigger focussing power, since it causes parallel incoming rays to be brought together over a shorter distance. It would be also straightforward to verify (try it yourself) that the focussing power is related to the lens curvature: the more "curvy" a lens is, the shorter its focal distance and the stronger its focussing properties (to get an additional intuitive feeling for this effect, it is often useful to think of the extreme cases: a "lens" with no curvature at all, i.e. a flat surface, has no focussing power at all, since the lens surface is everywhere perpendicular to incoming parallel rays, and no deflection occurs, or, if you prefer, the focal length is infinity).

Another thing to notice is that, if we have a flexible lens, we can increase its focussing power, i.e. decrease its focal length, by "squeezing"it, therefore increasing its curvature.

Putting it all together we can then say :
larger curvature = stronger lens = shorter focal distance
In many applications, especially the ones concerned with human vision, the strength of a lens in given in terms of the inverse of the focal length, When f is given in meters the lens power is measured in diopters, according to:
lens refractive power (in diopters) = 1/f
We can then extend the above summary line:
larger curvature = stronger lens = shorter focal distance = bigger diopter value
Focussing objects over a range of distances: eyes and cameras

We have seen that a converging lens can create an image (i.e. bring into focus) an object at a certain distance from it, according to
1/di+1/do = 1/f
which tells us that, once we have a lens of a given f, the position at which the object is brought into focus (=di) will depend upon the distance do of the object from the lens. But, ideally, it would be nice to be able to focus objects over a wide range of distances. From the expression above, we can see that this could be achieved in two ways:
1.
if the focal length of the lens is fixed, then we need to vary the relative position of lens vs. image: this is what is done in a photographic camera
2.
if the lens-image distance cannot be changed, then we need to have a lens with a variable focal length: this is what Nature chose to do in the evolution of the eye (at least this was her choice in our planet: some other life-form in another galaxy might have evolved eyes that pop out like in the cartoons...)
And how can one realize a variable-focus lens? Easily : if the lens is not rigid, we can change its focal length by stretching it or squeezing it, i.e. by changing its curvature.

In the (human) eye, the distance between lens and image forming plane (the retina, at the back of the eyeball) is fixed, with a value of about 1 inch, but the curvature of the lens is controlled by the ciliary muscle. When the muscle is relaxed, the eye-lens has its largest value of focal length (which is then equal to the lens-retina distance). In this situation, the lens is focussing onto the retina parallel light rays, i.e. rays coming from very far (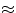$\approx$ infinitely far) objects. If the object distance is less than infinity, and the lens is not modified, the new image would be formed beyond the retina (reasoning : constant f means constant (1/di+1/do); if do is less than infinity, 1/do is larger than zero, therefore 1/di is smaller and di is bigger). To bring things back into focus, the muscle squeezes the lens to decrease its focal length to a new value f', so as to satisfy
1/di+1/do = 1/f'
But no matter how flexible the lens and how strong the muscle, there will be a limit to the smallest value of f than can be achieved : this will in turn set a limit to the nearest object that an eye can bring into focus. This distance is referred to as the eye's near point. Conversely, the furthest distance at which an object can be brought into focus is called the far point. For good eyesight, far point is at infinity, while typical values of near point are around 20-30 cm. But of course two things can occur:
1.
far point $<\infty$ : this is the case of myopia, whereby the eye cannot bring into focus distant objects
2.
near point larger than the regular values: this is the case of hyperopia (or presbiopia, "the eye of the old"), whereby the eye cannot focus at a near distance (as someone said, "it is not that my eyes are too weak, it is my arms that are too short"....).
Clearly, both of these conditions can be remedied with the use of corrective lens. For both cases the conceptual approach is the same: the required lens will be such as to form the image of an object wich lies outside of the eye focussing range within its range. Specifically: Angular Magnification

The expression we have found previously for the (linear) magnification, m = -di/do, is not very practical since it does not provide immediate information on the performance of a magnifying glass of a given focal length. In practice, magnification is more often expressed in terms of angular magnification, defined as the ratio between the angle, as seen by the eye, subtended by the magnified image and the angle subtended by the object when positioned at the near point. More specifically : if an object of height h is positioned at distance d from the eye, the angle subtended by the object is given by
$\tan\theta = h/d $
For not too large angles, this can be approximated as
$\theta \approx\tan\theta = h/d $
which shows the obvious fact that, if I move an object closer and closer to the eye (i.e. decrease d) the angle subtended becomes larger and larger (and of course the object appears to be bigger and bigger). But there is a limit to how close I can bring an object to the eye and still be able to see it, the limit being given by the near point N. The maximum angular size of a given object for the unaided eye will then be 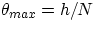$\theta_{max}=h/N$. To get a larger image of the object, we need a magnifying glass(i.e. a converging lens, with the object positioned "inside" the lens focal distance); in this case we can bring the object even closer.

If 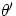$\theta '$ is the angle subtended in this configuration, we can still write $\theta ' = h/d$. Applying the definition of angular magnification M given above, we can say

$M = \theta '/\theta_{max} = (h/d)/(h/N) = N/d $
Now we make another approximation : if the magnifying lens is very near the eye, then the distance of the object from the eye is nearly the same as its distance from the lens (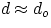$d\approx d_o$). Applying the thin lens equation we get
$M = N/d \approx N/d_{o} = N(1/f - 1/d_{i}) $
We are almost there, but we need to make a final choice: where do we want the lens image to be formed? In principle we could have it anywhere between the near point and infinity. Let's just stick with the two extremes :
1.
image formed at near point : in this case di=-N (remember : virtual image = negative di), therefore M = N/f+1 . You could verify that this choice gives the largest magnification, but is not desireable, since it requires the eye to be at its maximum "tension" (object is at near point)
2.
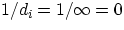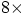image formed at infinity : in this case $1/d_{i} = 1/\infty = 0$, and the magnification becomes M = N/f. This expression is the one commonly used to express the power of a magnifying glass, with the implicit assumption that N = 0.25 m. If you see a lens rated at. e.g. $8\times$ this means that it provides an angular magnification of 8, which in turns must mean that it has a focal length of 3.1 cm, since
$ 8 = 0.25/f \longrightarrow f = 0.25/8 = 0.031 m = 3.1 cm $
We then learn that alternative ways of expressing the "power" of a lens are its focal length (measured in m), the inverse of the length (measured in diopters) or the angular magnification (a dimensionless quantity).
I will not go into details of multiple-lens system (e.g. microscopes and telescopes), but those of you taking the MCAT should be aware that I have seen microscope related questions in some sample test. Here are anyway a few general ideas that could be helpful in getting a feeling for such devices :
 
next up previous
Next: About this document ...
Sergio Conetti
3/27/2001