Chapter 27

Wave nature of light : Interference and Diffraction

Light is a wave. How can we tell? Simply by verifying that it exhibits interference phenomena. In fact, one can safely state:

1.

where there are waves there is interference

2.

where there is interference there are waves

In order to observe interference, we need the waves to have the same wavelength and to be in a well defined phase relation : the meeting of two waves that are perfectly in phase (i.e. both peak at the same time) will produce fully constructive interference while if the waves are 180⁰ (i.e. half a wavelength) out of phase we will have fully destructive interference. Any intermediate phase relation will produce partial (destructive or constructive) interference. The simplest way to observe interference (even without a laser) is to create a single beam of light (e.g. by sending light through a pinhole), letting this beam spread out and then cross two narrow slits (starting from a single beam guarantees that the two beams leave the two slits "in phase"). At some distance from the double slit, one can observe interference effects. What is the condition for constructive interference? Simply, the two beams will interfere constructively at any point where the difference in distance from the two slits is equal to any integer multiple of the wave's wavelength, 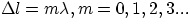$\Delta l = m\lambda, m = 0,1,2,3 ...$.

Similarly, the beams will interfere destructively whenever their distances from the slits differ by a half-integer number of wavelengths, 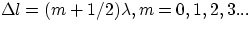$\Delta l = (m+1/2)\lambda, m = 0,1,2,3...$.If the slit separation is d, one could see that these conditions can be transformed into a condition for the exit angles corresponding to constructive (and destructive) interference, i.e.

• constructive interference $\sin\theta_{m} = m\lambda /d, m = 0,1,2,3,...$
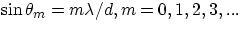
• destructive interference $\sin\theta_{m} = (m+1/2)\lambda/(d), m = 0,1,2,3,...$

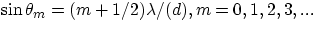
These expressions in turn can be used to determine the location of dark and bright bands on a screen positioned at a certain distance D from the slits, according to :

$y_{m} = D\tan\theta_{m}$

An important point to notice is that for the angular separation between bright and dark band to be sizeable, so that interference effects can be observed, the slit separation has to be comparable in size to the wave's wavelength. Conversely, knowledge of the geometry of a double slit setup and measurment of the separation between bright or dark bands allows to determine the value of light's wavelength.

These results do not just apply to light waves, but to any other type of electromagnetic wave (or any wave in general). An extremely important application was related to X-rays and the atomic structure. X-rays were first produced by shooting high energy electrons agains a target, but their nature was unknown (hence called X).

A key experiment performed around 1912 proved at the same time that X-ray were yet another form of electromagnetic waves, of very short wavelengths, and allowed to measure the spacing among atoms in a crystal. In the experiment, X-rays were directed towards a crystal, and the regular pattern of atoms in the crystal acted as a series of regularly spaced slits and produced a characteristic interference pattern. From this, one could determine the X-ray wavelength and infer that it was comparable in size to the crystal spacing. i.e. around 10^-10 m.

Iridescence

The variable colored patterns observed in oil slicks, soap bubbles, bird feathers, etc. are a consequence of interference between dfferent rays of reflected light. Specifically, let's think e.g. of a thin layer of oil on top of a water surface: light rays hitting the oil surface will be partially reflected and partially transmitted (i.e. refracted) through the surface. But the refracted rays, upon encountering the oil-water interface (i.e. the bottom part of the oil slick), will also be partially reflected. If the thickness of the oil film ha sthe right value, , i.e. it is of the order of light wavelength, one can expect interference between the two sets of reflected rays. In fact, you might be inclined to think that, for rays incident perpendicularly to the surface, destructive interference will be present whenever the path difference between the two rays is some odd number of half wavelengths, i.e. the thickness t of the oil layer is such that 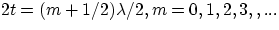$2t = (m+1/2)\lambda/2, m = 0,1,2,3,,...$, but in fact life is slightly more complicated than this, for two reasons :

1.

the fact that the speed of light is lower inside a medium implies that (rememebr that for any wave the speed is related to the wavelength, according to $v=\lambda f$) the wavelength inside a medium is also reduced, according to

$\lambda_{medium} = \lambda_{vacuum}/n$

2.

when a wave encounters an interface between two media of different n, the reflected wave is reversed (i.e. its phase is changed by 180⁰ or $\lambda /2$) whenever the refraction index of the second medium is larger than that of the first. A mechanical analogy is given by two pieces of ropes of different density (i.e. a light rope and a heavy rope) joined together. A pulse traveling along such a rope will be partially reflected when it reaches the junction point. The reflection will be upright when the pulse travels from the heavy to the light rope, while it will be upside down when going from light to heavy.

We can then consider different situations:

• thin film of index n surrounded by media of lower index (examples : thin transparent film in air(e.g. soap bubble), gasoline (n=1.4) over water (n=1.3), etc.). In this case, the ray reflected from the top has a phase flip, but not the one from the bottom. In practice, it is as if one of the two rays goes an extra distance of $\lambda /2$, so that the condition for destructive interference becomes
  $2t + \lambda/(2n) = (m+1/2)\lambda/(n), m = 1,2,3,...$
  $2nt = m\lambda +\lambda /2 -\lambda /2 = m\lambda, m = 1,2,3..$
• thin film of index n surrounded by media of higher index (example : thin air layer between two glass plates) : this situation is equivalent to the previous one, since a flip occurs at the bottom interface but not at the top, and one ends up with the same conditions for interference
• thin film of index n surrounded by a medium of lower index on one side and higher index on the other (e.g. oil between air and glass). Here both reflected rays undergo a phase flip, therefore the combined result is null, and the condition for destructive interference is the standard
  $2nt = (m+1/2)\lambda, m = 0,1,2,3$

From what we have seen, it is clear that, in a given situation constructive of destructive interference will be affected by 1) the thickness of the layer, 2) the light wavelength 3) the angle of light incidence. Consequently, different colours (i.e. different wavelengths) will be either enhanced or suppressed according to the (variable) thickness of the layer and the angle of vision.

Michelson interferometer: skip

Diffraction

We have seen how interference patterns will occur when combining light coming from two narrow slits. It turns out that interference phenomena will also occur when light crosses a single narrow slit. This phenomenon can be understood in terms of Huygens principle :

every point of a wave front can be thought of as the source of a wavelet, that propagates in all directions at the same speed as the actual wave

We can then think of what happens when a wave front encounters a small slit : consider the wavelet coming out of an edge of the slit; when viewing the wave coming out of the slit at some distance from it, there will be an angle for which the path of the wavelet coming from the edge and that one coming from the slit's center are $\lambda /2$ out of phase, therefore they will interfere destructively. But the same argument could be repeated for all other wavelets: at such an angle, every wavelet in the top half of the slit will have its interfering counterpart in the bottom half, and this will lead to fully destructive interference.There will then be a family of angles for which all of the light coming through the opening will cancel out. Similarly there will be a family of exit angles for which fully constructive interference occurs, and once again the image of a slit on a remote screen will be a succession of bright and dark bands. Simple geometry considerations would show that diffraction minima occur at angles such that

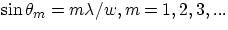$\sin\theta_{m} = m\lambda/w, m = 1,2,3,...$ w = slit width

Once again we see that observable effects will occur for slits's width comparable in size to the wave's wavelength. Notice that diffraction minima occur for m =1,2,3,... For m = 0. i.e. for the point directly in front of the opening, all the waveletes arrive in phase, therefore one has a bright diffraction maximum.

A similar phenomenon also occurs when light encounters a sharp edge, e.g. a small opaque disk. Wavelets from the disk's edge will propagate in all directions and, in particular, wavelets meeting at a point directly in front of the disk's center will all be in phase: a bright spot will appear where one would instead expect to see the shadow of the disk !!

Going back to the diffraction pattern associated with a small opening at a distance D from it, the width of the central bright maximum (i.e. the spacing between the left and right dark spots) is given by:

$2y = 2D\tan\theta \approx 2D\sin\theta = 2D\lambda/w$

showing that, at a given distance D, the width of the slit's image depends directly upon the wavelength, and inversely upon the magnitude of the opening. This has direct consequence on what is called resolving power : suppose you look at a distant bright object through a narrow opening (e.g. your eye's pupil). Diffraction causes the light through the opening to spread out, forming a pattern of a central bright image followed by a series of light and dark bands. If you now look at two distant objects, if the spreading is such that the images of the two objects overlap, then you will not be able to resolve the two images. A criterion for resolution was given by Lord Raleigh :

two distinct objects are not resolved if the first dark band of one falls onto the center of the second's bright central image

From what we have seen before, the minimum angular separation at which two distant objects can be resolved is then

$\theta \approx \sin\theta = \lambda/w$

with w being the slit width. When dealing with a circular opening, this expressions is modified to

$\theta = 1.22 \lambda/d$,

where d is the diameter of the opening. We can then see that shorter wavelengths are better resolved than longer ones, and resolution can be improved by increasing the size of the openings.