


Next: About this document ...
Chapter 29
Quantum Theory
The 20th century gave us a completely new, puzzling and unexpected way of
looking at the physical world, as described by the theories of
Quantum Mechanics and Relativity. An interesting difference between the two is
that, while Relativity was born "fully dressed", i.e. as a complete and mature
theory, Quantum Mechanics, had a very slow and gradual development, that is
continuing into the present age.
While both theories produce a very counter-intuitive and "unimaginable"
picture of the world, it is a fact that, in spite of its undisputable successes
and predictive power, as of today it is not really clear what
Quantum Theory really means, and the debate is still wide open about the
nature of physical reality, as described by the quantum rules.
As an anticipation to what we will learn, here are some of the major innovations
introduced by the quantum theory :
- 1.
- at the atomic and sub-atomic level, physical processes and physical
quantities are not continuous but quantized, i.e. they occur in discrete
chunks and/or steps. (Note : you are discreet if you mind your own business, while you are discrete if
you are made of small finite chunks)
In contrast, the whole body of Classical Physics is based on the idea of continuity. Calculus, which was
"invented" by Newton to express his description of the world, can be thought of as the mathematical
tool to describe continuous processes.
But we have already encountered a discontinuous process: when light is produced,
it is not accelerated from 0 up to c, but it instantenuously acquires its final
speed.
- 2.
- in the quantum picture, determinism has to be abandoned in favour of
uncertainty and probabilism. As it has been said, Nature does not know
what it will do next.
- 3.
- one of the most intriguing puzzles of the quantum world is the dual nature
(wave and particle) of both matter and radiation. How this can be is still an
open question.
But let us proceed in order : it all started, even though nobody at the time
realized it, with Max Planck, at the end of the 20th century. When studying radiation (Chapter 13), we had
seen that a body at a given temperature emits electro-magnetic radiation which depends uniquely on its
temperature. A systematic study would show that the emission spectrum has a distorted bell shape, with the peak of
the curve shifting to higher and higher frequencies as the temperature increases (think of a heating a metal rod
and observing the gradual shift of emitted radiation from infrared to red to blue light...). A cold body would emit
preferentially in the radio-wave range, while a super hot one would produce UV and X-rays.
The problem was that the observed spectra of radiation could not be explained in terms of Classical Physics, based upon ideas
of continuity. Trying to solve the problem, Planck realized that agreement with the data could be found by assuming that
radiation can be emitted only in integer multiples of a minimum unit.
Useful comparison: think of how there is a smallest unit for any given
currency, and payments can be made only in multiples of that unit. Obviously
if the fundamental unit is small enough, one is not aware of the
"quantization".
The smallness of the fundamental unit was certainly the case for the emission of radiation: to reconcile his model to the
data, Planck found that, for a given frequency f, energy was emitted in finite packets of energy quanta,
according to :
E = hf
where h is an exceedingly small constant, 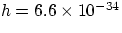 joule second.
joule second.
Planck presented his conclusions on Dec 14, 1900, and we like to identify that
date as the "birth of Quantum Mechanics" . Still, the event went largely unnoticed in the world of Physics.
The next episode in the saga sees again Einstein as a protagonist, and it involves the
photoelectric effect. After the 1896 discovery of the electron, physicists performed several studies of the properties
of this newly discovered constituent of matter. Among the new phenomena associated with it, it was seen that, shining light onto
a metal surface, electrons could be pulled out of the material. So far, nothing to be too surprised about : light waves, it was
well known, do carry energy, and it is not hard to imagine that, when this energy is transferred to an electron, it might
give it enough of a kick to free it from the binding force that keeps it inside the material. It is like surf pounding on a dam,
and getting some chunks of concrete off it...
The problem with the Photoelectric Effect was that it was not exhibiting a wave-like behaviour. As we have seen, the energy of a
wave (including electro-magnetic waves) is proportional to the (square of) its amplitude; in the case of light, this is in turn
related to the light's intensity. It was then logical to expect that the photo-electric effect could be enhanced by hitting the
metal with light of higher and higher intensity. But this was not what was observed : the observations showed that, for a given
metal, low frequency (e.g. red) light could not extract any electron no matter how intense the light source, while on the other side,
if the frequency was high enough (e.g. blue), even a very dim light could pull out the electrons. Moreover, when electrons were
extracted, their energy was not related to the intensity (i.e. the energy) of the incoming light, but again only to its frequency.
The quandary was resolved by Einstein : recalling Planck's results, he made the
hypothesis that light carries energy in well defined packets, each packet
carrying an amount E = hf. If we also assume that to pull an electron out of
the metal it takes an amount of energy above a certain minimum value, the
peculiarity of the photoelectric effect can be explained : if the energy of an
individual quantum of red light is not enough to pull out an electron, increasing their
number will not have any effect (except for the extremely unlikely occurrence of two or more quanta hitting the same electron within
a short time interval). On the other side, even a single blue photon could
do the trick. The energy of ejected electrons couls also be explained in terms of Einstein hypothesis:
let's call W0 the
minimum amount of energy required to free an electron from within a metal (one can think of a mechanical analogy : if an
object is inside a hole, I need to give it a minimum amount of kinetic energy to kick it out of the hole, this amount being the
difference in gravitational potential energy between the bottom and the top of the hole). Energy conservation than tells us that the
maximum kinetic energy an extracted electron can have is given by:
Emaxkin = hf - W0,
which does not depend upon the light's intensity but on its frequency. Light therefore, concluded Einstein, behaves like a particle.
Obviously, this interpretation could not be easily accepted, since it was very
well established that light was a wave. If questioned, Einstein would have
answered that he did not know how to reconcile the two pictures, but
nevertheless that was how nature behaved. Later experiments confirmed the
picture in full, even though nobody (including Einstein) can picture how something can be a wave and a particle at the same time.
Einstein, circa 1955 : fifty years of conscious brooding have brought me no nearer to the question
of "what are light quanta?". Nowadays every clod thinks he knows it, but he is mistaken
An equally compelling demonstration of the particle nature of light is given by the scattering of light off electrons: in 1923,
A. Compton, experimenting with X-rays, showed that the energy acquired by electrons when hit by X-rays was accompanied by a
decrease in frequency of the scattered X-ray, according to
Ekinelectron = hfin - hfout
which is what one expects from energy conservation if one treats the X-ray/electron interaction as a a standard "billiard ball"
elastic collision. This phenomenon (known now as the Compton effect) also allows to verify that photons, even though
massless, do carry momentum. From the relativistic expressions for energy and momentum, one has

and
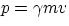
so that
E/p = c2/v
Even though this last expression refers to massive objects, one can ask whether it also applies to massless ones. In the case of
light, v=c, therefore:
that allows us to assign a momentum even to massless objects. By using this result, experiments would show that, as one expects
from elastic collisions, both energy and momentum are conserved in collisions between particles and radiation
The significance of the particle/wave duality of electromagnetic radiation is even more puzzling when one realizes that
one aspect or the other are brought into evidence depending on the experiment we do: it is as if light knew what we are trying to
measure.....
Here is a classic experiment : an ordinary beam of light contains extremely large numbers of photons (question : how many photons
per second are emitted by a 60 W light bulb? see Example 1 page 893), and we know that if we send such a beam through a double-slit
arrangement we will observe interference patterns.
But it is also possible to create a light beam of such low intensity, that only
a few photons per second are emitted. If we send such a low intensity light beam through the double slit, it is reasonable
to assume that each photon will go either through one slit or the other, but not both. Still, if we run the experiment long
enough, and we record, e.g. with a photographic film, the global distribution of photons on a screen at some distance from the slits,
again we would observe an interference pattern! How can a photon know not to go on a section of the screen where it would undergo
destructive interference with "future" photons? or does a photon maybe interfere with itself? To a large extent, these questions
remain unanswered as of today.
The interpretation of the double slit experiment with light is puzzling enough, but this is just the beginning.... As physicists
were compelled to accept this un-explainable dual nature of light (and electro-magnetic radiation in general), a French
prince-turned-physicist, Louis de Broglie, came up with an even more outrageous proposition
given that radiation is both wave and particle, wouldn't it be natural
to suspect that matter is also simultaneously particle and wave ?
This proposition by an unknown Physics Graduate Student, based on purely
theoretical grounds, was very revolutionary, but Einstein liked it, and that
was enough for it to be taken seriously. De Broglie proposal was to extend to ordinary matter the relation between momentum and
wavelength we have found for radiation
and to state that any object of momentum p = mv is at the same time also a wave of wavelength given by the expression above.
What does it mean that a material object (an electron, a proton, a cell, a
football, an elephant) is a wave, or, at least, has a wavelength/frequency
associated to it ? We (or at least I) don't know, but it is a fact that the
wave property of matter can be detected under the proper conditions. Not too long after de Broglie proposals, experiments
showed that beam of electrons, scattering off the regular lattice of a crystal do show interference patterns similar to those
prieviously observed with X-rays.
Remembering some of the facts we have learnt when studying wave optics, we can do a few numerical examples to see when and how
the wave nature of matter can be detected.....
The double slit experiment can be (and it has been) repeated for electron beams,
with equally inexplicable results: even though one electron at a time is going
through the slits, interfence patterns are observed. But one could add an extra
twist :
one can put a detector to determine through which opening the electron
is going through. If we do this, the electron "senses" that we are trying to
reveal its mystery, and it refuses to collaborate: when our experiment includes
some device capable of detecting the path of the electron, then the interference
pattern does not appear, and electrons behave as particles.....
The only possible interpretation of the double slit experiment is that, even
though each electron is bound to be going through only one slit, something else
must be going through both. This something else, which somehow contains
the wave-like nature of quantum objects, is what goes under the name of wave function.
What is the wave function? What is the meaning of the wave associated with particle-like objects? The best answer we have
found so far is that the wave function describing the evolution of a particle is
associated with the probability of finding the particle in any given location.
What Quantum Mechanics has taught us is that we cannot know for sure the outcome
of any single event, but we can only estimate its probability. One possible way to interpret quantum phenomena is to assume that,
when a given event occurs (e.g. an electron in a double slit experiment), all of the possible outcomes do take place,
according to their relative probability. In the double slit experiment, the
electron has a 50-50 probability of going through either slit, therefore the
global result will be consistent with it doing so ....
Unless of course we decide to observe the event : in this case, we force
the electron in one of its possible configurations, but as soon as we do that,
we destroy the probability function.... It is as if the Lottery drawings were
performed without the results being announced : in this situation,we could only
compute the probability of becoming millionaire. But if we demand that
the result be known, then only one of all the possible outcomes becomes reality.
In spite of this un-deterministic behaviour, the Quantum World has been shown
to obey a set of well determined rules. The first (and still very valid, for
non-relativistic phenomena) rigorous description of the quantum rules and the
evolution of the wave-functions associated with atomic and sub-atomic particles was due to Erwin Schroedinger.
Schroedinger's Equation can be thought of as the quantum's equivalent
of Newton's Law of Motion. It describes the behaviour and the evolution of the
wave function in the presence (or the absence) of a given field of force.
The equation is capable of describing phenomena like single and double slit
experiments, the behaviour of electrons within the atom (see next lectures),
weird phenomena like the tunneling effect, where a particle can find
itself outside of a hole even though it has not enough energy to do so, etc.,
etc.
But Schroedinger's success was bittersweet, since , even though he found the
correct equation, he never completely accepted its interpretation in term of
probability waves as opposed to real waves. But not even his cat was able to solve the riddle....
Heisenberg's Uncertainty Principle
The centerpiece of the un-deterministic scene of Quantum Mechanics is given by
Heisenberg's Uncertainty Principle, that quantifies the intrinsic limitations
in the accurate knowledge of the quantum world. Originally the principle was
motivated by a realization of the fact that the process of measuring an event
unavoidably affects it, but by now we realize that the principle has an
intrinsic validity, idependently of any observer's intervention.
The starting point, which is a direct consequence of wave-particle duality is the following: (see also the textbook for a
derivation involving the diffraction of a wave crossing a narrow slit)
suppose we want to determine the position of an object; to do so we must "see it", i.e. we must
hit it with a photon, and let the photon bounce back to our eyes. But, thinking
of the photon as a particle, this is like the collision between biliard balls:
by looking at the object we modify its velocity. Moreover, there is a standard
rule of optics, that states that the accuracy with which we can determine the
position of an object is limited by the wavelength of the radiation illuminating
it. The better we want to determine the position of an object, the shorter is
the wavelength we must use. But shorter wavelengths correspond to higher
frequencies, therefore to higher energies. The more precisely we try to determine the
position of an object, the more we alter its velocity....
Heisenberg was able to quantify these considerations, showing that the accuracy
with which we can simultaneously determine the position of an object along any given axis and the projection of its momentum
along the same axis is limited by the expression
Similarly, it can also be shown that an equivalent expression relates the energy of a particle and the time during which it can
have a given value of energy. This is in line with the 4-dimensional vision of the world of Einstein's relativity, since,
in relativity, the 4th component (i.e. the "time" component) of the momentum vector is in fact the energy. When applied to the
4th component, Heisenberg's principle reads
and again this result has ben veerified countless times in sub-atomic physics. As an example, "Particle Physics 101" tells us that
unstable particles, i.e. particles that can exist only for a finite  do not have a well defined value of mass, and the
shorter their lifetime the larger is the uncertainty in mass. In the sub-atomic world, one also routinely witnesses violation of
Conservation of Energy, but the violation is only allowed to occur over a limited time interval so as to be consistent with
Heisenberg's principle
do not have a well defined value of mass, and the
shorter their lifetime the larger is the uncertainty in mass. In the sub-atomic world, one also routinely witnesses violation of
Conservation of Energy, but the violation is only allowed to occur over a limited time interval so as to be consistent with
Heisenberg's principle 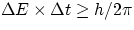 .
.



Next: About this document ...
Sergio Conetti
4/16/2001