


Next: About this document ...
Chapter 30
Quantum Theory meets the Atom
The early 1900's were probably among the most exciting period in the history of Physics, with new and revolutionary
facts and ideas following each other at a frantic pace. After Relativity and the onset of Quantum Mechanics,
another breakthrough came (in 1911) when an experiment by E. Rutherford revealed the inner structure of atoms. By
bombarding a thin gold foil with 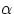 particles ( produced by the newly discovered phenomenon of radioactivity, and
now known to consist of two protons and two neutrons bound together) and observing that occasionally the projectiles
were deflected by a large angle, Rutherford concluded that most of the positive charge (and mass) of atomic matter was
concentrated in a very small central volume, while the carriers of the negative charge, the electrons, were
distributed at a very large distance from the central nucleus. Interpretation of Rutherford's results showed
that most of the atom's bulk was concentrated in a volume of
particles ( produced by the newly discovered phenomenon of radioactivity, and
now known to consist of two protons and two neutrons bound together) and observing that occasionally the projectiles
were deflected by a large angle, Rutherford concluded that most of the positive charge (and mass) of atomic matter was
concentrated in a very small central volume, while the carriers of the negative charge, the electrons, were
distributed at a very large distance from the central nucleus. Interpretation of Rutherford's results showed
that most of the atom's bulk was concentrated in a volume of 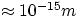 radius. This fact, combined
with the already exisiting knowledge that atoms radii were of the order of 10-10 m, led to the realization that
ordinary matter consists to a very large extent of purely empty space. In an often made comparison, if the atomic
nucleus was the size of a soccer ball, then the next nearer nucleus would be found at a distance of some 10 miles,
with all the space in between only occupied by some odd electron...
radius. This fact, combined
with the already exisiting knowledge that atoms radii were of the order of 10-10 m, led to the realization that
ordinary matter consists to a very large extent of purely empty space. In an often made comparison, if the atomic
nucleus was the size of a soccer ball, then the next nearer nucleus would be found at a distance of some 10 miles,
with all the space in between only occupied by some odd electron...
But the realization of the atomic structure was only the beginning : based on the known similarity between the
gravitational and the electrostatic forces, it was natural to assume that electrons orbited around the nucleus in a
fashion similar to the planets orbiting around the sun, but such a picture presented an intrinsic difficulty.
An object in orbital motion is subjected to (centripetal) acceleration and the (very successful) theory of
electromagnetism, as described by Maxwell's equations, taught that accelerated charges always emit radiation (to
convince you of how much faith existed in the correctness of Maxwell's equation, remember that Einstein preferred to
introduce his revolutionary new ideas on relativity rather than questioning Maxwell's validity). But conservation of
energy would cause the radiating electrons to gradually lose their energy, so that they could not maintain a stable
orbit, but they would eventually spiral down onto the nucleus (similarly, an artificial satellite in a near orbit will
dissipate its energy through collisions with residual air molcules, and gradually fall onto earth).
Another impasse had then been reached : reconciling Classical Electromagnetism with the newly found picture of the atom
required again some bold innovation. The decisive step was taken by Niels Bohr who took advantage of the newly emerging
ideas about quantization of the atomic world to explain at the same time both the behaviour of orbiting electrons and
the, until then mysterious, origin of the atomic spectral lines. What are they ?
It had been known for a long time that when energy was transmitted to a gas (either by heat or electricity), the gas
would emit electromagnetic radiation not in a continuous spectrum of wavelengths but only in some well defined group of
spectral lines of well defined wavelength (=colour, for the visible range). The simplest configuration was
encountered with Hydrogen, for which it had been recognized that radiation was emitted only in well defined "families"
of wavelengths, which could be described by purely empirical formulae:
Lyman series :
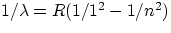
, n = 2,3,4,...
Balmer series :
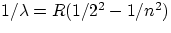
, n = 3,4,5,...
Paschen series :
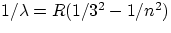
, n = 4,5,6,...
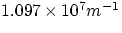 being a universal constant common to all the series (plugging in
the numerical values would immediately show that the three series correspond respectively to ultraviolet, visible and
infrared radiation).
being a universal constant common to all the series (plugging in
the numerical values would immediately show that the three series correspond respectively to ultraviolet, visible and
infrared radiation).
In spite of a large amount of experimental knowledge on the spectroscopy of Hydrogen and many other gases,
the physical mechanism responsible for such observed regularity was a complete mystery.
To solve the riddle of the Hydrogen atom, Bohr took advantage of the quantum idea that by then was receiving more and
more recognition. Pushing to a new level the concept that in the atomic and sub-atomic worlds the idea of continuity
had to be abandoned in favour of quantization, Bohr made the following proposal :
- electrons orbiting the nucleus could not have any arbitrary value of orbit radius, but only the ones corresponding
to a quantization of the angular momentum in units of Planck's constant h
- consequently, electrons could not emit radiation corresponding to any arbitrary value of energy, but could only
radiate quanta of energy corresponding to the energy difference between the allowed orbits.
In making such a proposal, Bohr had to reject the validity of Classical Electromgnetism, requiring that any accelerated
charge would radiate, since in his description of the atom electrons were undergoing (centripetal) acceleration without
this being accompanied by any radiation. But he felt that there was stonger and stronger evidence that the sub-atomic world
was subject to its own set of laws differing from those of the world perceived by our senses. For these reasons (as well as
his subsequent achievements) Bohr, rather than Planck or Einstein, is often considered to be the father of Quantum Mechanics.
Once you make the hypothesis of quantization of angular momentum of the orbiting electrons (i.e. that L = mvr can only
assume the values 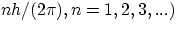 the derivation of the properties of the Hydrogen atom is very straightforward
(you could have done it yourself in a "double-starred" homework problem). Here are the steps :
the derivation of the properties of the Hydrogen atom is very straightforward
(you could have done it yourself in a "double-starred" homework problem). Here are the steps :
- 1.
- from the quantization condition
 one gets an expression for the velocity in the allowed orbits
one gets an expression for the velocity in the allowed orbits

- 2.
- to keep the electron in orbit, the Coulomb attractive force has to have the correct value to provide the appropriate
centripetal force. In formulae
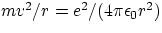 . Substituting for v one gets the values of
allowed radii as a function of purely the quantum number n and a bunch of constants:
. Substituting for v one gets the values of
allowed radii as a function of purely the quantum number n and a bunch of constants:
- 3.
- what we are interested is to find the values of energy relative to each allowed orbit. The total energy is the sum
of kinetic and potential energy:
Both r and v can be eliminated using the results from 1 and 2, and one ends up with an expression that depends uniquely on
n and a bunch of constants:
The negative value of E has to be interpreed as a potential energy, and it reflects the fact that a positive amount of
energy input is required to bring the electron at infinite distance (potential = 0) from the positive nucleus.
In its simplicity this result in a single sweep explains the mistery of spectral lines : an atom can emit energy only
in amounts corresponding to the difference in energy between two allowed orbits, i.e two orbits with
different values of n
This, together with Einstein's 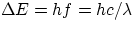 provides the full explanation for the origin of discrete
spectral lines, i.e.
One can just imagine Bohr's excitement when he verified that the product of the constants appearing in this expression was
exactly equal to the known value of the, empirically determined, Rydberg constant R !!
provides the full explanation for the origin of discrete
spectral lines, i.e.
One can just imagine Bohr's excitement when he verified that the product of the constants appearing in this expression was
exactly equal to the known value of the, empirically determined, Rydberg constant R !!
As important as the explanation of emission lines was the understanding of absorption lines : another fact known to
spectroscopist was that, when sending light ranging over a broad continuous spectrum of wavelengths through a gas,
certain frequencies would be absorbed, and in fact the absorbed frequencies did have the same values as the emitted
frequencies. In Bohr's picture, the same way that an atomic electron could perform a quantum jump from an orbit
of higher to one of lower energy by emitting a photon of the correct wavelength, then it could only absorb energy at the
values corresponding to allowed jumps from a lower to a higher orbit.
Bohr's results could easily be extended to atoms containing a number of positive charges larger than 1. In fact the only
required modification would be to add a term Z2 (with Z the number of positive charges) to the expression for the
allowed energy levels. In reality, in spite of its great achievements, it was soon seen that Bohr's model was not capable
of interpreting correctly the properties of atoms different from Hydrogen. Obviously a great step had been made in the right
direction, but more work was needed to arrive at the correct description of the atomic world. Moreover, in spite of its appealing
simplicity, we must be aware that the picture of particle-like electrons orbiting the nucleus like planets around the sun is
WRONG.
Atomic electrons and wave mechanics
The correct (as far as we can tell) description of the electron behaviour within the atom came from de Broglie's realization
that particles also have wave properties, and there is a direct connection between a particle's momentum and its wavelength.
Starting from this assumption, we can immediately find the physical motivation for the quantization of angular momentum, that
Bohr had treated as an ad hoc assumption. If particles are treated as waves, the condition for having a stable orbit is
that the orbit's length has to accomodate an integer number of wavelengths, i.e.
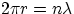
But, from de Broglie hypothesis, one has
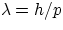
therefore, using the non-relativistic expression for p (in low Z atoms at least, electron speeds are well below c)
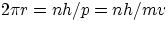
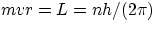
showing that the quantization of angular momentum is a direct consequence of the wave nature of the electron !!
Treating particles as waves is then done formally in Schrodinger's equation. By solving this equation for the case of an
electron in the force-field of the nucleus one gets, for the allowed energy levels, exactly the same result as had been obtained
by Bohr in more traditional approach to the Hydrogen atom. Moreover, the equation can correctly predict (albeit with non-trivial
mathematical difficulties) the correct energy levels for any arbitrary atom. But the success comes at a price, since the, mentally
appealing, Bohr picture has to be abandoned in favour of a much less intuitve picture, whose main features are
- electrons within the atom can only be described in terms of probability waves, that only tell us the
probability of an electron being at any given location with a given momentum (within the constraints of Heisenberg's uncertainty
principle, see Example 7 page 926). Electrons cannot be thought anymore as point
particles orbiting the nucleus at a fixed radius, but as probability clouds distributed over a certain volume, the shape of such
clouds being determined by the solutions of Schrodinger equation.
- the correct sequence of allowed energy levels does not depend any more on a single (as in Bohr's model) but on four
quantum numbers, again this result coming out of the solutions to Schrodinger's equation. The four quantum numbers, referred to
as n, l, ml and ms, are constrained to the following values :
- 1.
- n : 1,2,3,... corresponds to Bohr's original quantum number, and it still determines to a large extent the value of the
electron energy in any given shell (electrons with the same value of n are said to belong to the same shell)
- 2.
- l is associated with the electron's angular momentum, namely
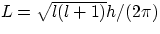 . l can only assume the values
0,1,2,...(n-1). In a given shell (i.e. for a given value of n), electrons with the same l are said to belong to the same
subshell
. l can only assume the values
0,1,2,...(n-1). In a given shell (i.e. for a given value of n), electrons with the same l are said to belong to the same
subshell
- 3.
- ml : this quantum number is associated with the orientation in space of the angular momentum, and it's bound to the
(integer)values
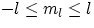 . The role played by ml becomes evident when the atom is within a region of magnetic
field: in the absence of a field, electrons with the same m and l but differing ml all have the same energy, but the field
induces small energy differences (from a spectroscopy point of view, the field splits a single spectral line into a multiplet
of closely spaced lines, Zeeman effect)
. The role played by ml becomes evident when the atom is within a region of magnetic
field: in the absence of a field, electrons with the same m and l but differing ml all have the same energy, but the field
induces small energy differences (from a spectroscopy point of view, the field splits a single spectral line into a multiplet
of closely spaced lines, Zeeman effect)
- 4.
- ms : this is the spin quantum number. A useful mental picture (which is nevertheless most likely meaningless
in terms of the "real" behaviour of the electron) is to think of electrons having angular momentum by
spinning around their axis. With respect to a given direction, the spinning can be clockwise or counter-clockwise, therefore the
spin quantum number can only assume two values, -1/2 and +1/2 (in units of h/2
 ).
).
These four quantum numbers determine the preferred arrangements of electrons within the atom, which in turn
determines the chemical properties of different atoms. Chemical properties (and the Periodic Table of
Elements) can be fully understood in terms of the quantum numbers and the following rules :
- 1.
- in the absence of external influences, electrons will assume the configuration corresponding to the lowest energy (i.e.
corresponding to the lowest values of quantum numbers)
- 2.
- Pauli exclusion principle: no two electrons in an atom may have the same four quantum numbers
- 3.
- chemical properties of an element are determined mainly by the electrons in the "outermost" subshell
- 4.
- the most stable (chemically speaking) configuration for an atom is to have its outermost subshell completely filled (or
completely empty, which is the same.... an element with only one electron in its outermost subshell will willingly give it
away, while an element one electron short will willingly acquire an extra electron....etc.)
X-rays
Understanding of the atomic structure and of the emission of radiation by means of quantum jumps allowed to explain
another experimental fact, i.e. the spectrm of X-rays. X-rays (which we have seen are electromagnetic radiation of higher
energy than UV) are produced by accelerating electrons up to some tens of thousands of electron-volts, and smashing them agaist
some metal target. Upon hitting the target, electrons can do two things
- 1.
- interacting with the electric field of the nuclei, electrons will undergo the equivalent of "elastic collisions" and will
lose some
or most of their energy. But the "deceleration" process has to be accompanied by radiation, therefore electrons going through
some material will emit electromagnetic radiation in a continuous spectrum of frequencies, up to a maximum value corresponding
to the electron total kinetic energy
- 2.
- alternatively, speeding electrons can knock out an electron from one of the atoms. This process would leave the atom in an
unstable condition, and soon one of the electrons from a higher orbit will fall down to fill the vacated location, In doing
so, it will emit a characteristic quantum of radiation of energy corresponding to the energy difference between the two levels
In summary, high speed electrons going through some material will produce EM radiation whose spectrum should consist of a
continuum distribution plus some narrow discrete lines, and this is exactly what is observed for the X-ray. Experience has shown
that the most prominent line is the one corresponding to an electron from the K-shell (n=1) being knocked out, followed by
an n=2 electron dropping in to fill the void. To get an approximate value for the energy of the corresponding radiation, one
can still use Bohr's formula for a nucleus with Z protons , i.e. 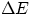 (in eV) = 13.6 Z2(1/1-1/4).
To account for the screening of the nuclear charge due to the other electrons it has been shown that
one should replace Z2 with (Z-1)2 . Given that Z uniquely identifies a chemical element, bombarding
a sample of unkown composition with high energy electrons and measuring the wavelength (i.e. the frequency, i.e. the energy)
of emitted X-rays can be used to detect even minute amounts of the elements contained in the sample.
(in eV) = 13.6 Z2(1/1-1/4).
To account for the screening of the nuclear charge due to the other electrons it has been shown that
one should replace Z2 with (Z-1)2 . Given that Z uniquely identifies a chemical element, bombarding
a sample of unkown composition with high energy electrons and measuring the wavelength (i.e. the frequency, i.e. the energy)
of emitted X-rays can be used to detect even minute amounts of the elements contained in the sample.
Conventional X-ray vs. CT scans. X-rays have been extremely useful in medical diagnostics, but one limitation of
a conventional X-ray picture is that it provides a flat (i.e. two-dimensional) picture of the body under exam. A full
three-dimensional reconstruction can instead be obtained by means of the CAT scan (CAT : Computer Assisted (or Axial) Tomography,
Tomography: "picture by the slices", "tomo" is the same greek root as atom, "the one that cannot be sliced"). The basic idea of a
CAT scan is to "illuminate" the body under exam from many different orientations; feeding all the information to a computer it is
possible to create a stereoscopic image of the subject.
Lasers
The normal state (ground state) for an atom is with all of its electrons in the lowest shells (lowest energy), but when
the atom is exposed to some energy source, one or more of its electrons can be boosted to some excited state. But this is an
unstable configuration, and soon the atom will
decay back (with accompanying photon emission) to the ground state. Under normal conditions, the exact timing of the return to
the ground state cannot be predicted (only the probability of it happening within a given time interval can be calculated), but,
in a special circumstance, the release of radiation can be controlled : if a photon of the right energy (i.e. the energy
corresponding to an allowed transition) goes by an electron in an excited state, the electron will be "tickled" to perform the
transition to ground at the exact instant as the other photon goes by. One photon coming in will then result in two photons
coming out. Moreover, these two photon will have exactly the same wavelength and will be "coherent" i.e. in phase, so that they
will always intefere constructively. This is the phenomenon of stimulated emission, which is exploited for
Light Amplification by Stimulated Emission of Radiation (notice that the term "amplification" is a bit of a misnomer ; a laser
does not really amplify energy, but it converts disordered, random energy into ordered coherent energy). Once we understand the
principle of stimulated emission, it is quite straightforward to understand the laser's principle of operation. Here are the
basic steps :
- 1.
- a gas contained into a cylinder is excited by sending some electric current through it, so that severla electrons go into
an excited state
- 2.
- when an atom drops down to the ground level, the emitted photon has some probability of inducing another transition
in another atom. When this happens, we have two coherent photons
- 3.
- these two photons can in turn liberate two more photons from two other excited atoms, so now we have four....
- 4.
- the process would not go very far if we did not provide the means of
- (a)
- replenishing the supply of excited atoms and
- (b)
- maintaning the ever growing beam of coherent photons
Requirement (a) is satisfied by maintaining the exciting agent (i.e. the electric current through the gas): this is called
pumping the laser. Requirement (b) is achieved simply by making the
endcaps of the cylinder with reflecting material, so that the coherent laser beam goes back and forth inside the cylinder.
- 5.
- finally, we want to get the intense beam out of the cylinder. To achieve this, it is enough to make one of the endcaps
of some material which is partially reflecting and partially transparent, so as to allow part of the beam to exit.
This all sounds very simple, and in a sense it is, but there are some complications. The bigger one is that, in general, an atom
stays in an excited state for a very short time (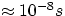 ), so that in general it would tend to decay spontaneously
(and randomly) before having the chance of producing the stimulated emission. But there are some special excited states (
metastable states) with much longer lifetimes (
), so that in general it would tend to decay spontaneously
(and randomly) before having the chance of producing the stimulated emission. But there are some special excited states (
metastable states) with much longer lifetimes (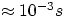 ), which, in the atomic world is an eternity. When
atoms are excited to a metastable state, then the chance of inducing stimulated emission are greatly enhanced, and lasing
can take place.
), which, in the atomic world is an eternity. When
atoms are excited to a metastable state, then the chance of inducing stimulated emission are greatly enhanced, and lasing
can take place.
Sections 30.9 and 30.10 : read for your own culture (especially 30.9)



Next: About this document ...
Sergio Conetti
4/23/2001
![]() (in eV) = 13.6 Z2(1/1-1/4).
To account for the screening of the nuclear charge due to the other electrons it has been shown that
one should replace Z2 with (Z-1)2 . Given that Z uniquely identifies a chemical element, bombarding
a sample of unkown composition with high energy electrons and measuring the wavelength (i.e. the frequency, i.e. the energy)
of emitted X-rays can be used to detect even minute amounts of the elements contained in the sample.
(in eV) = 13.6 Z2(1/1-1/4).
To account for the screening of the nuclear charge due to the other electrons it has been shown that
one should replace Z2 with (Z-1)2 . Given that Z uniquely identifies a chemical element, bombarding
a sample of unkown composition with high energy electrons and measuring the wavelength (i.e. the frequency, i.e. the energy)
of emitted X-rays can be used to detect even minute amounts of the elements contained in the sample.