


Next: About this document ...
CHAPTER 10
Rotations
You might not have realized it, but until now all the objects whose motion we studied
(divers, cats, airplanes, etc.) were actually treated as dimensionless
"point-like" objects. This is because, even though the objects had some non-zero size, we
only considered translational motions, ignoring any possible rotation (a geometrical point,
having no spatial extension cannot rotate around itself..). But now we are ready to analyze
the more realistic situations that include both rotations and translations. To start, we
remind ourselves of the "natural" unit for measuring angles, i.e. the radian:
given an angle, the ratio between the arc it subtends and the radius of
the arc is always the same, regardless of our choice for the radius. One then defines as the
measure of the angle (in radians) the ratio between arc length s and radius r

(in radians) =
s/
r
Being the ratio between two lengths, radians are dimensionless. Converting radians to and from degrees
is easily accomplished via
radian / degree =
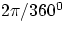
,
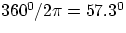
Rotational Variables
Even though in principle rotations can be described in terms of displacements,
velocities and accelerations, it soon becomes obvious that these are not the most convenient quantities,
for the following reason :
consider e.g. a rigid disk rotating around an axis going through its center; in a given time interval,
a point at the disk's edge covers a longer distance than a point nearer the center : for a rotating
body, velocity is not a well defined quantity, since it depends on the location of the point under exam.
On the other side, in a given time interval, the angle swept by a radius joining the center of rotation
with any arbitrary point is the same, regardless of the point's location. Rotations can then be better
described in terms of angular, rather than linear, variables. We then define :
Are angular velocities scalars or vectors? This is equivalent to asking : can we associate a given
rotation with a direction in space? The answer is yes : a rotation is identified by the axis of rotation.
We then adopt the convention of assigning to the angular velocity vector 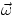 the direction
of the rotation axis. The vector orientation will be chosen so that, if you lie along the axis, the
vector going from your feet to your head, then the rotation appears to be counterclockwise (see also
right hand rule).
the direction
of the rotation axis. The vector orientation will be chosen so that, if you lie along the axis, the
vector going from your feet to your head, then the rotation appears to be counterclockwise (see also
right hand rule).
Once we define  as a vector, then also
as a vector, then also 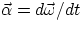 is a vector. If
the (angular) acceleration has only the effect of changing the magnitude of the angular velocity, then
is a vector. If
the (angular) acceleration has only the effect of changing the magnitude of the angular velocity, then
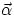 will be parallel (or anti-parallel) to
will be parallel (or anti-parallel) to 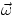 , but if the orientation of the
rotation axis also changes, then the direction of
, but if the orientation of the
rotation axis also changes, then the direction of 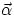 is given by the direction of the vector
difference
is given by the direction of the vector
difference 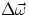 .
But note that rotations themselves cannot be defined as vectors, since they are not well behaved : when
dealing with rotations,
.
But note that rotations themselves cannot be defined as vectors, since they are not well behaved : when
dealing with rotations, 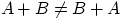
Relation between angular and linear quantities
NB : for the following expressions to be valid, angles MUST be measured in radians
Let's consider an arbitrary point on a rotating body, located at a distance r from the rotation
axis. When the point covers an arc s, one has  and, consequently:
Using these results, one could readily obtain, for the case of a rotation with constant angular
acceleration
and, consequently:
Using these results, one could readily obtain, for the case of a rotation with constant angular
acceleration 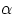 , kinematic expressions completely equivalent to the ones we had obtained for
linear motion with constant acceleration:
and, eliminating the time variable
(see e.g. example 10.2 for a complete application of these formulae).
Advice : even though rotational problems are formally identical to linear motion problems, conceptually
they might appear less intuitive. It is recommended to do a few such problems to gain familiarity)
, kinematic expressions completely equivalent to the ones we had obtained for
linear motion with constant acceleration:
and, eliminating the time variable
(see e.g. example 10.2 for a complete application of these formulae).
Advice : even though rotational problems are formally identical to linear motion problems, conceptually
they might appear less intuitive. It is recommended to do a few such problems to gain familiarity)
In the past, we had already learnt something about rotations, when we were dealing with circular
motion. In fact, now we can define uniform circular motion as a motion characterized by constant
angular velocity  . We had also learnt that uniform circular motion is characterized by
a centripetal acceleration ac=v2/r.
Question: in a uniform circular motion with centripetal acceleration ac, what is the angular
acceleration
. We had also learnt that uniform circular motion is characterized by
a centripetal acceleration ac=v2/r.
Question: in a uniform circular motion with centripetal acceleration ac, what is the angular
acceleration 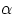 ????
????
The answer is clearly zero: uniform circular motion, by definition, has a constant
 , and we have just seen that
, and we have just seen that 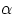 represents the rate of change of
represents the rate of change of  ....
But not all circular motions are uniform, we can have a situation where the angular velocity is
changing, which also means that the magnitude of tangential velocity for any given point of the
rotating object will change, since
....
But not all circular motions are uniform, we can have a situation where the angular velocity is
changing, which also means that the magnitude of tangential velocity for any given point of the
rotating object will change, since 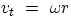 . But if the magnitude of vt is changing, we
must have a tangential acceleration at, which, as seen before is related to the angular
acceleration by
. But if the magnitude of vt is changing, we
must have a tangential acceleration at, which, as seen before is related to the angular
acceleration by 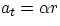 . Therefore, in general, the acceleration of a point on a rotating object
is given by
. Therefore, in general, the acceleration of a point on a rotating object
is given by
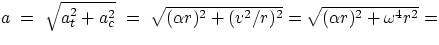

In summary:
- uniform circular motion has constant angular velocity, constant centripetal
acceleration and zero tangential (and/or angular) acceleration
- rectilinear motion has zero centripetal acceleration, all acceleration is "tangential"
- non-uniform circular (or, in general, non-rectilinear) motion has a centripetal
acceleration (with instantaneous value
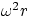 , where
, where  is the instantaneous angular
velocity) and a tangential (therefore angular) acceleration. The global acceleration vector is given by
the vectorial sum of centripetal and tangential accelerations.
is the instantaneous angular
velocity) and a tangential (therefore angular) acceleration. The global acceleration vector is given by
the vectorial sum of centripetal and tangential accelerations.
Rotational Energy
How much kinetic energy is carried by a rotating object? To find this out, we first notice that, if an
element of mass dm at a distance r from the axis of rotation is moving with velocity v, its kinetic
energy is
The total energy of the rotating object will then be the sum of all the infinitesimal energies, i.e.
where we define the moment of inertia 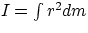 .
We conclude that, when dealing
with a rotating object, we can express the (rotational) kinetic energy in terms of its angular velocity,
provided we replace the mass with the moment of inertia.
When dealing with a set of
discrete objects rather than a continuous distribution, the moment of inertia is simply
where the ri's are the distances of the masses mi from the rotation axis. We can
immediately draw some conclusions:
.
We conclude that, when dealing
with a rotating object, we can express the (rotational) kinetic energy in terms of its angular velocity,
provided we replace the mass with the moment of inertia.
When dealing with a set of
discrete objects rather than a continuous distribution, the moment of inertia is simply
where the ri's are the distances of the masses mi from the rotation axis. We can
immediately draw some conclusions:
- when dealing with rotations the moment of inertia is somewhat the equivalent of the mass in linear
motions. We can then expect that it will somehow represent the resistance a given object opposes to be
put into rotation
- as it will become more and more clear, this "rotational inertia" will depend on the distance of the
masses from the axis of rotation
- the moment of inertia is not an intrinsic property of a given object, since its numerical
value depends upon the choice of axis of rotation
Calculation of I
How can one evaluate the integral 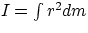 , since the differential is a mass while the function is
a position? Obviously one needs to find a relation between masses and positions: remembering the definition of
density
, since the differential is a mass while the function is
a position? Obviously one needs to find a relation between masses and positions: remembering the definition of
density 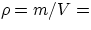 for an infinitesimal volume element = dm/dV, therefore
and, if the body is homogeneous,
this might not always be easy to compute, but at least only contains spatial variables. When one or two
dimensions of the object under exam are negligible (thin sheet or long thin rod) it is often useful to
introduce the surface density
for an infinitesimal volume element = dm/dV, therefore
and, if the body is homogeneous,
this might not always be easy to compute, but at least only contains spatial variables. When one or two
dimensions of the object under exam are negligible (thin sheet or long thin rod) it is often useful to
introduce the surface density 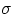 or the linear density
or the linear density 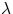
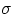
= mass per unit area =
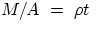
t = thickness
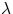
= mass per unit length =
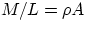
L = length, A = area
Examples :
- thin rod of length L rotating around one end (similar to example 10.6) :
if 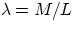 , then
, then  , therefore
, therefore
- thin rectangular metal plate (area = a b) rotating around side a
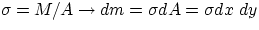
I will not expect you to be able to compute complicated integrals, but I do expect you to be aware and be able to
apply the
Parallel Axis Theorem:
given the moment of inertia ICM around an axis going through the center of mass, and the moment of inertia
I around an axis going through an arbitrary point but parallel to it , the two are related by
I = ICM+Md2
where d is the distance between the two axes
TORQUES
You have been told that an object is in equilibrium (i.e it has no acceleration)
when the net force acting on it is zero. Obviously you were told a lie,
since it is easy to think of many situations where a body is accelerating even
if no net force is present (think e.g. of a water sprinkler with two jets
spurting in opposite directions: the two jets exert equal and opposite forces,
but when you turn the water on the sprinkler strats rotating...).
The reason for this ambiguity is that the statement about forces in equilibrium
only applies to translations (or if you prefer, to point-like objects)
and it ignores the possibility of rotations. How do then forces come into play when
dealing with rotations, therefore angular, as opposed to linear, accelerations?
When a body is free to rotate around a point (or, to be more precise, around an
axis), it is a well known fact that the force inducing rotations will be the more
effective the larger is the distance between the point where the force is applied
and the axis of rotation (compare what happens if you try swinging a door by
pushing near the hinges or near the handle). Also, you will be much more effective
in opening the door if the force is perpendicular rather than parallel to the door.
We formalize these intuitive concepts introducing the following quantities:
- given a force, we call line of action the direction along which the
force is acting
- given a force (with its line of action) and an axis of rotation, we call
moment arm (or lever arm) the perpendicular distance between line of action and
axis of rotation.
- finally we define as torque
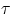 the product of force magnitude
times lever arm,
the product of force magnitude
times lever arm, 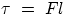 .
.
By convention, torques are positive when they would cause a counter-clockwise rotation.
Be clear that torques are not absolute quantities, but their numerical value
depends upon the choice of axis of rotation.
The fact that when dealing with rotations what matters is not just the force but
rather the torque has obviously been applied since antiquity: just think of wrenches,
levers, etc...
If a torque is what causes rotations, then we can immediately guess that
a body will be in complete equilibrium (i.e. no accelerations) when both the
net force and the net torque are zero
The first condition guarantees the absence of linear, i.e. translational, accelerations,
while the second implies no angular, i.e. rotational, accelerations.
Newton's Law for Rotational Dynamics
Let us consider a body free to rotate around an axis, and let us apply to it
a force F perpendicular to the axis and at a certain distance from it (so that the
lever arm is not zero). For an infinitesimal volume of mass dm located
at a distance ri from the rotation axis we can write
dF =
dm a
dF r =
dm ar
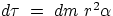
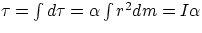
which is analogous to F = ma, provided one replaces forces with torques, masses with moment of inertia
and linear acceleration with angular acceleration. Notice that an essential step in the derivation was the
factoring of 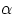 outside the integral : while the linear acceleration is different for each element of the
rotating body, the body as a whole has the same angular acceleration.
outside the integral : while the linear acceleration is different for each element of the
rotating body, the body as a whole has the same angular acceleration.
Among many other applications, the formula above allows us to estimate the moment of inertia for a body of
arbitrarily complex shape. How ? by applying to it a known torque and measuring its angular acceleration.
Work, Power and all that
We have already seen the expression for kinetic energy associated with rotations:
Let us recall what we had learnt in terms of work,power, etc. for translational motions :
one could easily see that all of these expressions have their rotational equivalents :



Next: About this document ...
Sergio Conetti
10/16/2000
![]() , and we have just seen that
, and we have just seen that ![]() represents the rate of change of
represents the rate of change of ![]() ....
But not all circular motions are uniform, we can have a situation where the angular velocity is
changing, which also means that the magnitude of tangential velocity for any given point of the
rotating object will change, since
....
But not all circular motions are uniform, we can have a situation where the angular velocity is
changing, which also means that the magnitude of tangential velocity for any given point of the
rotating object will change, since ![]() . But if the magnitude of vt is changing, we
must have a tangential acceleration at, which, as seen before is related to the angular
acceleration by
. But if the magnitude of vt is changing, we
must have a tangential acceleration at, which, as seen before is related to the angular
acceleration by ![]() . Therefore, in general, the acceleration of a point on a rotating object
is given by
. Therefore, in general, the acceleration of a point on a rotating object
is given by