


Next: About this document ...
CHAPTER 11
Rolling, rolling, rolling ...
When an objects rolls (without slipping) along a surface, you are simultaneously witnessing a rotation
and a translation. To be precise, as seen from an observer at rest, the correct motion is an
instantaneous rotation around the contact point (with the position of the rotation axis therefore
advancing continuously), but it is easier to analyze the motion dividing it into a translation and
a rotation around the wheel's axis.
- 1.
- rotation : as it rotates around its axis, all the points of the wheel have the same angular velocity
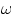 . The tangential velcity of a point on the rim is
. The tangential velcity of a point on the rim is 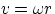 , and it points forward for a
point at the top of the wheel and backwards for a point at the bottom
, and it points forward for a
point at the top of the wheel and backwards for a point at the bottom
- 2.
- translation : the first thing to notice is the the center of the wheel (its center of mass for a well
balanced wheel) is always on top of the contact point. Therefore when the wheel's edge rotates by an arc
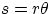 the wheel's center advances by an equal amount. The wheel center then moves with velocity
and, from the translational point of view, all the points of the wheel move forward with speed
the wheel's center advances by an equal amount. The wheel center then moves with velocity
and, from the translational point of view, all the points of the wheel move forward with speed 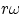 .
.
to get the global motion of the wheel we have to combine the two motions and we get :
- a point at the top of the wheel has instantaneous velocity
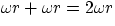
- the point in contact with the ground has instantaneous velocity
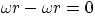 , it is
not moving !!
, it is
not moving !!
- the center of the wheel moves at the wheel translational speed
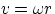
Energy Budget How much kinetic energy is carried by a rolling object ? As its motion is a
rotation around the contact point, its kinetic energy is 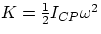 , where by
ICP we mean the moment of inertia with respect to the contact point. But the Parallel Axis Theorem
tells us ICP = ICM + Mr2, therefore
the total kinetic energy is the sum of its rotation energy around the center of mass plus the
total translational energy of the rolling body. In other words, when I do some work to get something
rolling, part of the work goes into rotational energy and part into translational energy.
, where by
ICP we mean the moment of inertia with respect to the contact point. But the Parallel Axis Theorem
tells us ICP = ICM + Mr2, therefore
the total kinetic energy is the sum of its rotation energy around the center of mass plus the
total translational energy of the rolling body. In other words, when I do some work to get something
rolling, part of the work goes into rotational energy and part into translational energy.
Question : if two bodies start from the top of a slope, and one slides down while the other rolls
down, which one will reach the bottom first?
Vector (or "cross") Product
If  , then
, then 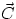 is a vector of magnitude
is a vector of magnitude 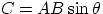 , with
, with
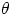 = angle between
= angle between 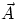 and
and 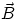 , direction perpendicular to the plane containing
, direction perpendicular to the plane containing
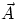 and
and 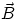 , and orientation given by the "right hand rule".
, and orientation given by the "right hand rule".
[hint : if the orientation of the vectors make it awkward to properly orient the right hand (or if you have an
accident just before the test and have to put your right hand into a cast) remember that you can use your left
hand, and flip the direction so obtained]
Properties:
Torques as Vectors
Earlier on we have found the relation 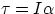 , which we had written as a relation among scalars. But
we had also assigned a vector nature ta the angular acceleration
, which we had written as a relation among scalars. But
we had also assigned a vector nature ta the angular acceleration 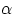 . Simplest case :
. Simplest case :
rigid body rotating with variable speed around a fixed axis z : 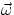 is always parallel to z,
therefore both
is always parallel to z,
therefore both 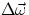 and
and 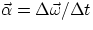 are parallel to the
rotation axis.
are parallel to the
rotation axis.
We would be tempted to write 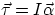 , and in fact this expression would be correct if we
define the torque as
, and in fact this expression would be correct if we
define the torque as  , where
, where 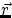 is the vector coordinate of the point of
application of the force causing the torque. Is this consistent with our earlier definition of torque?
is the vector coordinate of the point of
application of the force causing the torque. Is this consistent with our earlier definition of torque?
- 1.
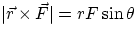 , with
, with 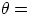 angle between
angle between 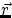 and
and 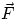 . But
. But
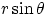 is exactly the perpendicualr distance between the force's line of action and the reference point
is exactly the perpendicualr distance between the force's line of action and the reference point
- 2.
- again thinking of the simplest case of a disk rotationg around its center, we see that the effective force
producing the rotation is tangent to the disk and perpendicualr to the disk radius. Their vector product will be
directed along the perpendicular to the disk's surface, which is also the direction of

We then see that the expression 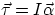 , with
, with  is fully
satisfied both in magnitude and direction.
is fully
satisfied both in magnitude and direction.
Angular Momentum
Remembering that we had defined the linear momentum as 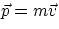 , and we had the relation
, and we had the relation
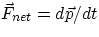 , as well as the important rule of conservation of (linear) momentum, we can expect
similar results for rotational variables. We start by defining the angular momentum of a single particle
with respect to a point O as
where
, as well as the important rule of conservation of (linear) momentum, we can expect
similar results for rotational variables. We start by defining the angular momentum of a single particle
with respect to a point O as
where 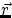 is the (instantaneous) position vector of the particle with respect to the reference point O.
Notice that
is the (instantaneous) position vector of the particle with respect to the reference point O.
Notice that
angular momentum is meaningful even for the case of rectilinear motion
(we can interpret a linear motion in terms of rotations by realizing that, as the body moves along, 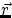 rotates
around O.
rotates
around O.
Simplest case: mass m in uniform circular motion on circle of radius r :  , and
the direction of
, and
the direction of  is along the perpendicular to the plane of the circle. One also has
which is the rotational equivalent of
is along the perpendicular to the plane of the circle. One also has
which is the rotational equivalent of 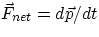 .
.
Notice that in the expression above  and
and 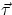 have to be evaluated with respect to the same point
O, and this point must belong to an inertial frame (i.e moving with constant velocity).
have to be evaluated with respect to the same point
O, and this point must belong to an inertial frame (i.e moving with constant velocity).
Angular Momentum for a system of particles : the extension is immediate, if we have n particles, each
one having angular momentum  , the total angular momentum of the system will be
A few remarks :
, the total angular momentum of the system will be
A few remarks :
- we had seen in the past that, because of Newton's third law, for any system
 .Can we also say that in general
.Can we also say that in general 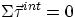 ? The answer is yes, provided we realize that the
forces acting between two bodies lie along the line joining them, therefore they have the same line of
action and consequently the same moment arm with respect to any arbitrary point.
? The answer is yes, provided we realize that the
forces acting between two bodies lie along the line joining them, therefore they have the same line of
action and consequently the same moment arm with respect to any arbitrary point.
- like before, torques and angular momenta have to be evaluated with respect to the same point, and this point
must belong to an inertial frame
- exception: the above expressions are still valid when the reference point is the center of
mass of the system, even if it is moving with some acceleration (e.g. free falling). Examples : the angular
momentum around the center of mass of a vaulting acrobat, a somersaulting gymnast, a rotating diver, etc. is
constant even though the center of mass is accelerating, therefore not in an inertial frame.
Angular momentum of a rotating rigid object
It is my belief that, in the attempt to simplify the matter, your textbook's section 11.4 is misleading and
confusing : compare e.g. the caption of fig 11.12 ("when a rigid body rotates around an axis the angular
momentum L is in the same direction as the angular velocity") with the footnote in the same page, stating that
this claim is in fact non-valid. And the statement that the angular momentum has only components parallel to
the rotation axis is not justified (in fact it is in general wrong), and is obtained by considering only a thin
slice of the rotating object (compare fig. 11.12 with handout). Here is the correct story :
- For an arbitrary body rotating around an arbitrary axis, in general the total angular momentum is not
parallel to the rotation axis (simplest example and useful exercise: look at fig. 11.14, and pretend that it is
rotating around the y axis rather than in the plane of the page. Can you tell what would be the direction of the
angular momentum?)
- in general, one can still evaluate the magnitude of the component of the angular
momentum parallel to the rotation axis z with the result
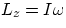 .
.
- in the special case when the body rotates around an axis of symmetry (going obviously through the center
of mass),then L = Lz and
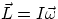
If we limit ourselves to this last simple case, in the absence of external torques, we have 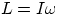 = constant . If, in some way, a rotating object changes its moment of inertia I, then
= constant . If, in some way, a rotating object changes its moment of inertia I, then
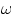 will change too, so as to keep their product constant.
will change too, so as to keep their product constant.
Sections 11.6, 11.7 : skip



Next: About this document ...
Sergio Conetti
10/20/2000