


Next: About this document ...
CHAPTER 12
Static equilibrium
Practically the whole of Chapter 12 can be summarized by
a body will be in complete equilibrium (i.e. no accelerations) when both the
net force and the net torque are zero
The first condition guarantees the absence of linear, i.e. translational, accelerations,
while the second implies no angular, i.e. rotational, accelerations.
A legitimate question: we know that the condition 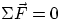 is independent of the choice
of reference axes. But what about the torques ? Torques are defined with respect to a given point, so even if the
torques add up to zero with respect to a given point, couldn't their resultant be non-zero with respect to
another point?
is independent of the choice
of reference axes. But what about the torques ? Torques are defined with respect to a given point, so even if the
torques add up to zero with respect to a given point, couldn't their resultant be non-zero with respect to
another point?
Fact : if the vector sum of a set of forces is zero, then the vector sum of their torques is the same
regardless of the reference point
note that I am saying that the sum of the torques is the same, not that it
is necessarily zero. One could obviously have a situation where the forces add up to zero, while the torques
do not. But if the torques are 0 with respect to a given point, they will be zero with respect to any point,
and the body will be in both translational and rotational equilibrium, i.e it will be moving with constant
(possibly 0) linear velocity and constant (possibly 0) angular velocity.
Proof : assume 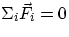 . With respect to an arbitrary point O1, the torque sum is
If we now choose a point O2, we have
but, if
. With respect to an arbitrary point O1, the torque sum is
If we now choose a point O2, we have
but, if 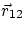 is the position of O2 with respect to O1,
is the position of O2 with respect to O1, 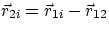 ,therefore
due to the fact that
,therefore
due to the fact that 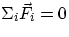
Special case : what is the condition of equilibrium for a body supported at one point and under the sole influx
of gravity?
Since one can assume that the force of gravity is applied at the body's center of mass, for the torque to be
zero then the moment arm with respect to the support point has to be zero, i.e. gravity's line of action has to
go through the point of support. Therefore the body will be in equilibrium when its center of mass is exactly
above (or below) the support point.
The conditions 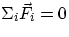 and
and 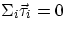 can in general lead to a fairly
complex situation (the two vector equations correspond to six equations among the components). In many cases
the problem can be reduced to a two-dimensional one : if all the applied forces are coplanar, i.e.
they belong to the same plane (let's say the xy plane), then the conditions to be satisfied for equilibrium are:
Examples : Problems 12.16,12.41
can in general lead to a fairly
complex situation (the two vector equations correspond to six equations among the components). In many cases
the problem can be reduced to a two-dimensional one : if all the applied forces are coplanar, i.e.
they belong to the same plane (let's say the xy plane), then the conditions to be satisfied for equilibrium are:
Examples : Problems 12.16,12.41
Section 12.4 : read and digest. I will not discuss it, nor include it in the tests, but it is useful information



Next: About this document ...
Sergio Conetti
10/20/2000