


Next: About this document ...
CHAPTER 13
Simple Harmonic Motion
We have already learnt that when a spring is stretched or compressed by a certain amount x, it exerts
a force proportional to the displacement. Moreover, the direction of the force exerted by the spring is
always opposite to the displacement (and for this reason it is called a restoring force). All this
can be expressed by
F = -kx
with k = spring constant. We will now study the motion of a body moving under the influence of such a
restoring force. This motion, that goes under the name of Simple Harmonic Motion (or Simple
Harmonic Oscillation), is encountered, either exactly or approximately, in a very large class of
physical phenomena.
Suppose then you have a mass m resting on a frictionless surface and attached to a spring of constant k.
To obtain the equation of motion, we write as usual Newton's second law :
F=ma
-kx(t) = m d2x(t)/dt2
this is again a differential equation, and to solve it we need to find a function which, apart from the
constant factors k and m, is equal to minus its second derivative. The minus sign is
essential, and if it wasn't there it would lead to a completely different situation.
Question : what would be the solution if the minus wasn't there, i.e. if you were looking for a function
equal to its second derivative?
But returning to our case, we see that a good candidate is the cosine (we could also have chosen the sine),
since
We can then guess that the cosine is the function we are looking for, and in fact one could see that the
most general expression satisfying the differential equation under study can be written as
with  constant parameters. We can verify that this result satisfies the differential equation.
One has
But the condition we want to satisfy is
constant parameters. We can verify that this result satisfies the differential equation.
One has
But the condition we want to satisfy is
a(t) = -(k/m)x(t)
our general solution will satisfy this condition provided that 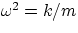 .
.
It is clear then that the motion of our mass will be a periodic oscillation, with the mass moving back
and forth around its position of equilibrium x=0.
Let us examine the physical meaning of the parameters  :
Let us choose for simplicity
:
Let us choose for simplicity  The expressions
allow us to determine the position, velocity and acceleration of our mass, as well as their relative values,
at any instant t. In particular :
The expressions
allow us to determine the position, velocity and acceleration of our mass, as well as their relative values,
at any instant t. In particular :
- velocity and position are always 900 out of phase. Velocity is at a maximum when
x=0 (i.e. the mass goes through the position of equilibrium); what is its value at this point?
On the other side, velocity is 0 when x is at a (positive or negative) maximum. This is the way it should
be, since the positions of maximum displacement correspond to the points where the velocity changes sign.
- position and acceleration are 1800 out of phase : at any instant they are proportional to
each other but opposite in sign, a=-(k/m)x . When the mass goes through the position of equilibrium (x=0)
then also a=0 . Why should the acceleration be 0 at that point?
Harmonic Motion and Energy Coservation
We had learnt that the force exerted by a spring is conservative and that a spring stretched (or compressed)
by an amount x carries a Potential Energy 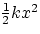 . We can then expect that, throughout the
oscillatory motion, the total mechanical energy (i.e. the sum of potential + kinetic energy) of the system is
conserved :
. We can then expect that, throughout the
oscillatory motion, the total mechanical energy (i.e. the sum of potential + kinetic energy) of the system is
conserved :
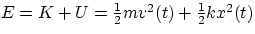
= constant
Throughout the motion we have a continuous, back and forth transformation from potential to kinetic energy and
viceversa. When the spring is fully stretched (x=xmax) the energy is all potential, while when the mass
goes through x=0, the potential energy is zero and the energy is all kinetic. We then have
(and the last equality shows again that 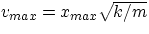 ). Through simple substitutions one could
also see that
Pendulum
Another mechanical system moving with simple harmonic motion is the pendulum: as an immediate consequence,
we can expect that the pendulum period of oscillation will be independent of the oscillation amplitude. This
important property was first realized by Galileo when observing the swinging of the church chandeliers as the
sexton
). Through simple substitutions one could
also see that
Pendulum
Another mechanical system moving with simple harmonic motion is the pendulum: as an immediate consequence,
we can expect that the pendulum period of oscillation will be independent of the oscillation amplitude. This
important property was first realized by Galileo when observing the swinging of the church chandeliers as the
sexton![[*]](http://www.phys.virginia.edu/usr/icons.gif/foot_motif.gif) was snuffing out the candles, and led to the construction of the first reliable time-keeping devices.
was snuffing out the candles, and led to the construction of the first reliable time-keeping devices.
The conceptual pendulum is a point-like mass m supported by a massless string of length l. The forces acting
on the mass are gravity and the string tension. As usual, the string tension cancels out the radial component
of gravity, so that the only unbalanced force, responsible for the motion of the mass is gravity's tangential
component  .
. 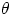 is the angle with respect to the vertical and the minus sign
reflects the fact that the force is alwyas in the direction opposite to the displacement (therefore it is a
restoring force). Newton's law will then give
this equation is not equivalent to that of the harmonic oscillator, since it relates the second derivative of
is the angle with respect to the vertical and the minus sign
reflects the fact that the force is alwyas in the direction opposite to the displacement (therefore it is a
restoring force). Newton's law will then give
this equation is not equivalent to that of the harmonic oscillator, since it relates the second derivative of
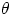 not to
not to 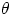 itself but to its sine, and its solution is not straightforward. But we can
simplify it by noticing that, if
itself but to its sine, and its solution is not straightforward. But we can
simplify it by noticing that, if 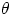 is small enough (say less than 100), then
is small enough (say less than 100), then  (in radians, you can verify it on your calculator). The expression therefore reduces to
whose solution will then be
with
(in radians, you can verify it on your calculator). The expression therefore reduces to
whose solution will then be
with 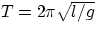 , showing that, for small oscillation, the period is independent of the
amplitude but is determined purely by l and g .
, showing that, for small oscillation, the period is independent of the
amplitude but is determined purely by l and g .
When dealing with a physical pendulum rather than an ideal one, the length l is obviously given by the distance
between the point of suspension and the pendulum center of mass (since there is where the force of gravity is
applied). With a given pendulum therefore one can either
- 1.
- measure g if l is known, or
- 2.
- given g, determine the center of mass of the swinging body (if you want to locate your own center of
mass, you can ask a friend to hang you by your feet and time the period of your oscillations)
In terms of angular variables, the pendulum equation can be written as
which represents an oscillation of period 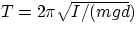 . This would allow to determine the moment of
inertia of any object, provided the location of its center of mass is known.
. This would allow to determine the moment of
inertia of any object, provided the location of its center of mass is known.
Torsional Pendulum Grandfather clocks are awkward to be worn on your wrist or kept in your pocket.
To build a (mechanical) watch you need to rely on torsional elasticity : if you twist an elastic material
(e.g. a wire) by an angle 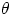 , the restoring force creates a torque which is proportional to the angle of
twist,
, the restoring force creates a torque which is proportional to the angle of
twist, 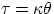 . If allowed to oscillate, a body attached to a twisted wire will oscillate with
period
. If allowed to oscillate, a body attached to a twisted wire will oscillate with
period 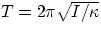 .
.
Harmonic Motion as Projection of Circular Motion In describing the harmonic motion, we have used the
symbol 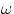 , which is normally associated with an angular velocity. So far we can just assume that the
quantity
, which is normally associated with an angular velocity. So far we can just assume that the
quantity 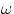 was used for convenience, to avoid the
was used for convenience, to avoid the 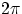 factors that would appear if we were to express
the harmonic motion in terms of period T or frequency f. But we'll see that one can conceptually associate
a harmonic motion with a uniform circular motion.
Consider a body in uniform circular motion with constant angular velocity
factors that would appear if we were to express
the harmonic motion in terms of period T or frequency f. But we'll see that one can conceptually associate
a harmonic motion with a uniform circular motion.
Consider a body in uniform circular motion with constant angular velocity 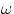 . As the body moves around the
circle, its projection on the x-axis is
where, for simplicity, we have chosen
. As the body moves around the
circle, its projection on the x-axis is
where, for simplicity, we have chosen 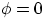 . We then see that the projection of a uniform circular
motion on any axis moves with simple harmonic motion. If we also look at the projection on the y-axis, its
motion will be given by
. We then see that the projection of a uniform circular
motion on any axis moves with simple harmonic motion. If we also look at the projection on the y-axis, its
motion will be given by 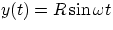 . Since the global motion is given by the combined motion
along the x and y direction, we can then state that
any uniform circular motion can be considered as the combination of two simple harmonic motions along
orthogonal directions and out of phase by 900.
. Since the global motion is given by the combined motion
along the x and y direction, we can then state that
any uniform circular motion can be considered as the combination of two simple harmonic motions along
orthogonal directions and out of phase by 900.
Damped Oscillations In any real life situation, a harmonic oscillation will not go on forever,
but it will gradually come to a stop, since the original mechanical energy gets eaten away by friction, air
resistance etc. We have already seen that, under certain condtions, motion through a fluid encounters a
resistance R which is proportional to the velocity of the moving object R = -bv . To study the motion of a
harmonic oscillator under these more realistic conditions, we must include this resistive forcce in the
equation of motion :
-kx-b dx/dt=m d2x/dt2
this differential equation is slightly more complicated than the one we encountered before, and so is its
solution, which turns out to be
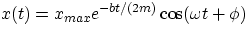
,
with
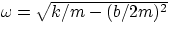
telling us that
- if b is small, then the solution reduces to the undamped oscillation
- the effect of the damping is to cause an exponential decrease of the oscillation amplitude as well as to
move the frequency of oscillation away from its natural frequency =
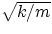
- the time it takes for the oscillations to completely die away, as well as for the number of oscillations
before stopping depends on the relative values of b, m and k.
- when
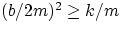 , the system does not oscillate any more (negative square root). Under these
conditions, when moved away from the position of equilibrium it will return there without oscillating.
, the system does not oscillate any more (negative square root). Under these
conditions, when moved away from the position of equilibrium it will return there without oscillating.
It could be shown that the condition (b/2m)2=k/m corresponds to the shortest time for returning to
equilbrium. This condition is called critical damping. If b is smaller than the critical value
the system is underdamped, if larger overdamped.
Forced Oscillations Another interesting case is when a force is applied to a system in
order to keep it oscillating.
Note : so far we have dealt with the ideal case of a mass m attached to a spring k, leading to a natural
angular frequency 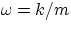 . In reality, practically every object has some elasticity and, if some energy
is applied to it, it will tend to vibrate at a well defined frequency. In other words, every object has some
well defined natural frequency of vibration
. In reality, practically every object has some elasticity and, if some energy
is applied to it, it will tend to vibrate at a well defined frequency. In other words, every object has some
well defined natural frequency of vibration 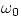 (and in fact complex objects can have several natural
frequencies)
(and in fact complex objects can have several natural
frequencies)
If now we want to transfer some energy to a system to keep it vibrating even in the presence of some resistive
force, it is intuitive that the most efficient situation is encountered when a periodic force is applied with
a period close to the natural period of the oscillating system.
Think of maximizing the amplitude of a swing: if
you give it random pushes, sometime you will increase its velocity but sometime you will decrease it. But you
will reach optimum performance if you push it in synchronism with the swing oscillating motion.
Solution of the appropriate diferential equation, including restoring force -kx, damping force -bv and periodic
applied force 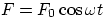 leads to a sustained oscillation of amplitude
showing that the largest amplitude is obtained when
leads to a sustained oscillation of amplitude
showing that the largest amplitude is obtained when 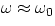 . In fact, if the damping is small,
amplitude can become infinitely large.... The condition
. In fact, if the damping is small,
amplitude can become infinitely large.... The condition  is called resonance, and
it is encountered in several fields of physics (acoustics, electric circuits, subatomic physics, etc.)
is called resonance, and
it is encountered in several fields of physics (acoustics, electric circuits, subatomic physics, etc.)



Next: About this document ...
Sergio Conetti
10/31/2000
![]() . We can then expect that, throughout the
oscillatory motion, the total mechanical energy (i.e. the sum of potential + kinetic energy) of the system is
conserved :
. We can then expect that, throughout the
oscillatory motion, the total mechanical energy (i.e. the sum of potential + kinetic energy) of the system is
conserved :