


Next: About this document ...
CHAPTER 14
Universal Gravitation
You are probably aware that Newton's greatest achievement was to deduce that between any two
objects of mass m1 and m2 separated by a distance r there is force of magnitude
F=Gm1m2/r2
and obviously the force of 1 on 2 is equal and opposite to the force of 2 on 1. Vectorially, if 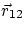 is
the unit vector directed from 1 to 2, then the force of 1 onto 2 is given by
where the minus sign indicates that the force has the direction opposite to
is
the unit vector directed from 1 to 2, then the force of 1 onto 2 is given by
where the minus sign indicates that the force has the direction opposite to 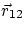 , therefore it is
an attractive force.
The 1/r2 dependence appears in several physical situations, and is related to the fact that the surface of a
sphere is proportional to the square of the radius. Semi-rigorous argument:
, therefore it is
an attractive force.
The 1/r2 dependence appears in several physical situations, and is related to the fact that the surface of a
sphere is proportional to the square of the radius. Semi-rigorous argument:
position a mass m at the center of a sphere of radius r1: because of the symmetry, the strength of the force
will be equal at any point on the sphere's surface. With a bit of poetic licence, we could say that the force is
"uniformly spread" on the surface. If we call 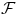 the "total force available", then the "force per unit
surface" is
the "total force available", then the "force per unit
surface" is 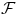
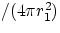 . At a larger distance r2 the same quantity will be
. At a larger distance r2 the same quantity will be
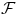
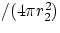 . We can make our unit surface as small as we like, typically a point, therefore we see
that the force at any given point decreases like the inverse square of the distance from the source of the force.
. We can make our unit surface as small as we like, typically a point, therefore we see
that the force at any given point decreases like the inverse square of the distance from the source of the force.
Consequences and applications of Newton's Law of Gravitation are countless, we will quickly go through some of
the main ones:
- why do all bodies fall at the same rate, regardless of their mass ? (after all mass is a measure of inertia,
and one might expect that a more massive object has more inertia, therefore it is less easily accelerated).
Answer: because the force that causes the fall is actually proportional to the mass of the falling object. If M is
the mass of the Earth, R its radius and m the mass of the falling object
a = F/m = (GmM/R2)/m = GM/R2 = constant
and this constant is what we have called g
- the expression g= GM/R2 allows to determine the mass of the earth provided G and R are known. The
radius of the earth was known since antiquity (clever procedure by Eratostenes), but an independent measurement
was neccessary to determine G. This was done by Cavendish in 1798 with a delicate experiment measuring the force
between two large masses. When performing his experiment, Cavendish liked to say that we was "weighing the earth".
- Kepler's law : sorting out a great wealth of data on planetary motion, Kepler was able to come up with his
three laws
- 1.
- all planets move in elliptical orbits, with the sun at one of the foci
(circle : locus of points equidistant from a given point called the center
ellipse : locus of points whose sum of distances from two given point (foci) is constant.
the circle is a "degenerate" ellipse")
the planet orbits are not very "eccentric", for many applications one can assume they are circular
- 2.
- in its motion, a planet sweeps equal areas in equal times
- 3.
- the square of the orbital period is proportional to the cube of the orbital radius
Kepler was very proud of his discovery, even though he had no idea of the motivation behind his laws. But they can
be obtained as very straightforward consequences of Newton's equations:
- 1.
- Law 1 : we will not prove it, but one could see that it is a direct consequence of the 1/r2 behaviour of
the force
- 2.
- Law 2 : this law would be automatically true for an exactly circular orbit, but one can se that it is equally
valid for elliptical orbits. It is best proved by realizing that since the force acting on a planet has 0 torque (as
the force is always directed toward the center of rotation the lever arm is zero), then the planets angular momentum
is constant. See the book for the rest of the proof.
Conservation of angular momentum allows us to compute the velocity at a point of the orbit if the velocity at another
location is known (see example 14.5). We could immediately see that
an orbiting body will move faster when nearer the attracting center, slower when further. As we will
verify later, this is also true for orbits of different radii: the larger the radius, the smaller the speed
This might be counterintuitive since you might have thought that far away planets have to move faster since
they have a much larger orbit. But think in the following terms :
what prevents a planet from falling onto the sun (or the moon onto the earth, etc.)? Obviously it is its "tangential
inertia", i.e. the fact that the orbiting body has a certain speed and, in the absence of a force, it would tend to
fly away along the tangent. But the closer the body is to the attracting center, the larger is the force, therefore
you need a larger velocity to maintain "rotational equilibrium".
- 3.
- Law 3: for a planet mp at a distance r from the sun ms, in the circular orbit
approximation F=ma will give :
from this we see that,to have a stable orbit,we cannot arbitrarily choose both orbital period and orbit radius:
for a given radius the period is uniquely fixed and viceversa (geosynchronous satellites can only be positioned at
a well defined distance from the earth)
Example : if there was no air resistance, you could shoot a projectile horizontally off the top of Mt. Everest and put
into a stable orbit. What would be the period of revolution? and what initial speed should you give to the
projectile?
Gravitational Field
Gravity, like another force of Nature, Electromagnetism, extends out to infinity ( a suggestive quote : pick up a flower
on earth,and you move the furthest star...), and, apparently, its effect is felt instantaneously.
How can such an action at a distance occur? Until recently there was no answer, altough nowadays we believe that
all forces are
transmitted by a carrier, the complete explanation being contained in state of the art Quantum Field Theories. Still,
physicist were able to circumvent the question by thinking in terms of a gravitational field :
if you start
with empty space, and then put a mass m0 somewhere in it, this mass will modify the previously empty space by
generating a gravitational field extending out to infinity. In other words, at any point in space, another mass will
feel a force  , where
, where 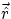 is the unit vector pointing from m0 to
m. But we would like to characterize the effect of the mass m0 independently of the value of m. We can do that
by stating that the mass m0 generates, at any point in space, a gravitational field of strength g = F/m =
-Gm0/r2.
Like the force, the field is a vector, and, in our case, it points towards the mass generating it (i.e. the field has
the same direction as the force). This definition can be then generalized to describe the field due to a discrete
collection of masses as well as to a solid object (like e.g. the earth). What is the gravitational field due to the
earth? As long as we stay outside of the earth's surface it is
is the unit vector pointing from m0 to
m. But we would like to characterize the effect of the mass m0 independently of the value of m. We can do that
by stating that the mass m0 generates, at any point in space, a gravitational field of strength g = F/m =
-Gm0/r2.
Like the force, the field is a vector, and, in our case, it points towards the mass generating it (i.e. the field has
the same direction as the force). This definition can be then generalized to describe the field due to a discrete
collection of masses as well as to a solid object (like e.g. the earth). What is the gravitational field due to the
earth? As long as we stay outside of the earth's surface it is  .
(The better you understand this and the following concepts now,the better you'll be able to handle electromagnetic
fields).
.
(The better you understand this and the following concepts now,the better you'll be able to handle electromagnetic
fields).
Gravitational Potential Energy revisited
Under the assumption that force of gravity was constant, we had defined the gravitational potential energy at a height
h above a reference level as U=mgh. When we start dealing with planetary motion, etc. our simplifying assumption
is not any longer valid. To obtain the correct expression, we must use the correct definition for potential energy
associated with a (conservative) force between two masses m1, m2

-
Gm1m2/
r + constant
where the value of the constant depends on our choice of reference level. As we will only be interested (either
explicitely or implicitely) in potential energy differences, the constant plays no role. In fact, we can get rid of
the constant by realizing that the force is zero at 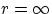 , and choosing our reference level such that also
, and choosing our reference level such that also

Such a choice (that results in the gravitational potential energy always being negative) has an interesting
interpretation:
suppose you have two masses at a distance r1 from each other. As the force of gravity is attractive, if I want to
increase their separation I have to do some positive work W, which will be equivalent to the change in potential
energy of the system, 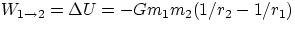 . How much work do I need to do
to completely separate the two masses ? If they are originally at a separation r the work is
. How much work do I need to do
to completely separate the two masses ? If they are originally at a separation r the work is
the potential U(r) can then be thought of as the binding energy for the system of the two masses since its
magnitude represents the amount of work (i.e. the amount of energy) I would need to provide to fully separate the
two particles. Another way to look at it is to state that the the two particles are bound since they do not
have enough energy to be separated, and, if they were to be separated the energy would have to come from some agent
external to the system.
We can extend these ideas by including the kinetic energy. For simplicity, we will study planetary and satellitar
situations, where one lighter object of mass m is orbiting a much heavier M, so that almost all of the kinetic energy
is carried by the light orbiting mass.
The total energy of the system (which ,as we are dealing with a conservative force,
will be constant) is
E = K + U = 1/2 mv2-GmM/r
but mv2/r = ma = F = GmM/r2, therefore
K = 1/2
mv2 =
GmM/(2
r)

we then see that
- the kinetic energy is (in magnitude) half of the potential energy
- the sum of the two is therefore always negative, as it should be for a bound system. In fact, if the kinetic energy
was to exceed at any time the potential energy, then one would have enough kinetic ebergy to bring the two masses at
infinite separation, and still have some kinetic energy leftover
- the velocity is inversely proportional to the (square root of the) radius: as discussed earlier, larger radii
correspond to smaller velocities.
- like before, the total (negative) energy of the system represents the binding energy, since, to separate the
two masses, I would have to provide an amount of energy at least equivalent in magnitude to the energy of the system
Application : escape velocity and black holes.
If I have an object of mass m initially at rest on the surface of a celestial body of mass M and radius r, how much
initial velocity should I give to it if it was to escape out to infinity ?
The condition is
But we can also see that insome case there is no escape. If the celestaial body is massive enough and small enough, one could
have a situation where 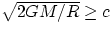 , where c is the speed of light. Given that nothing (not even light) can
go faster than c, nothing, not even light, could escape: we are dealing with a black hole .
, where c is the speed of light. Given that nothing (not even light) can
go faster than c, nothing, not even light, could escape: we are dealing with a black hole .
Sections 14.9, 14.10 : we will skip them now, but you will probably have to face them in PHYS 232, so you might want to look
at them to get a feeling of things to come. Also example 14.10 is particularly intriguing.



Next: About this document ...
Sergio Conetti
11/3/2000
![]() . How much work do I need to do
to completely separate the two masses ? If they are originally at a separation r the work is
. How much work do I need to do
to completely separate the two masses ? If they are originally at a separation r the work is