


Next: About this document ...
Chapter 15
Fluid Mechanics
reminder : density 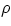 of a given substance defined as the mass of a unit volume
Measuring
of a given substance defined as the mass of a unit volume
Measuring 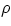 in kg/m3, is not very convenient, since it yields fairly large numbers for
ordinary materials (1 m3 is a relatively large volume), more commonly one expresses densities
in g/cm3 or in terms of specific gravity, i.e. the ratio between the density of the
substance and the density of water. Given that
in kg/m3, is not very convenient, since it yields fairly large numbers for
ordinary materials (1 m3 is a relatively large volume), more commonly one expresses densities
in g/cm3 or in terms of specific gravity, i.e. the ratio between the density of the
substance and the density of water. Given that 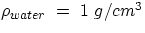 , specific gravity is
numerically equal to density measured in g/cm3.
, specific gravity is
numerically equal to density measured in g/cm3.
Question: isn't it strange that the density of water (at 40 to be precise) is exactly 1
g/cm3? Any idea why ?
Remember that densities vary with pressure and temperature. The variation is not
very big for solids and liquids, but is quite sizeable for gases.
Pressure
In the following we wil make ample use of a new quantity, the pressure,
defined as the force per unit surface. If I have a solid object
(e.g. a cylinder) of mass m resting on a table, and A is the area of contact, then the pressure it exerts
on the table is, if h is the height of the cylinder,
P = F/A = mg/A =
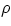
V g/A =
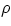
ghA/A =
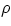
gh
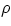 gh, with
gh, with 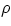 the liquid density and h its level above the
bottom.
the liquid density and h its level above the
bottom.
More precisely, if the pressure at a certain depth h1 is P1, then the pressure at a depth 2 will
be
So far so good, but things become less intuitive if I put some object within the volume of the
liquid. Let's start by putting a flat fish like a flounder in the water, and let's assume that it
is at rest; from what we just
said, its upper surface must feel a pressure 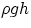 , where h is the depth of the flounder. But,
given that it is at rest, there must be an equal and opposite pressure acting on its lower surface.
And the result would have been the same if I had taken a round fish: if it is at rest, the same force per
unit surface must be felt by every section of its surface.
, where h is the depth of the flounder. But,
given that it is at rest, there must be an equal and opposite pressure acting on its lower surface.
And the result would have been the same if I had taken a round fish: if it is at rest, the same force per
unit surface must be felt by every section of its surface.
These simple arguments could be generalized and verified by accurate measurements, leading to the conclusion
that a fluid exerts on all the surfaces of a submerged object a pressure which is perpendicular
to the surface itself and numerically equal to 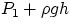 , where P1 is the pressure at the surface
and h the depth of the submerged object.
, where P1 is the pressure at the surface
and h the depth of the submerged object.
A legitimate question would be: if the pressure at a given depth of a fluid is due to the weight of the column of
fluid above, how can a force be exerted in any direction and not just in the vertical direction?
The answer is that, in a fluid, pressure is due
to the motion of the molecules and their collisions against each other or against any
submersed object or even against the walls of the container. Think of a container full
of liquid : even though it is clear that the walls feel a pressure (if they weren't strong enough
the container would burst), this cannot be directly due to the weight of the liquid, since the
weight force is parallel to the side walls. The idea of fluid pressure being due to collisions by
fluid molecules is even more clear if we think of a gas. The walls of a gas filled balloon undoubtedly
are feeling a pressure, but this is obviously not due to the weight of the gas...
But sometimes the weight of a gas cannot be ignored : the column of air above us is
high enough, that its weight, and its pressure, are not negligible. Can we estimate the
magnitude of atmospheric pressure? The expression 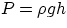 , with
h the height of the air column (some tens of kilometers), would not give the right answer, since
the density is not constant (you all know that there is "less air" at higher altitudes).
, with
h the height of the air column (some tens of kilometers), would not give the right answer, since
the density is not constant (you all know that there is "less air" at higher altitudes).
But atmospheric pressure can easily be measured, and this
was done for the first time by Evangelista Torricelli, a student of Galileo, who was asked to figure
out why one could pump water out of mines only up to a height of about 10 meters. The belief of the
time was that water pumps worked since they created a vacuum above the water surface, and water then
rushed in to fill the vacuum (Natura abhorret vacuum). Torricelli instead realized that the agent was
the atmospheric pressure, and in doing so he produced the first (mercury based) barometer.
Atmospheric pressure is quite useful, without it we could neither sip a drink through a straw, nor
use shaving cream....
For historical reasons, many different units are used for pressure: the correct SI unit is the pascal
1 P = 1 N/m2, but other units are mm (or inches) of mercury, atmospheres, bars, pounds per square
inch (psi)... 1 atmosphere = 760 mm Hg ; how much is that in pascals or psi's?
Absolute pressures can be measured with a Torricelli-like barometer, but often it is more convenient
just to measure the pressure excess (or defect) with respect to the atmospheric pressure: this
quantity is called gauge pressure. To measure gauge pressure one can use an open ended,
mercury filled, U-shaped tube, one end of which is connected to the pressure under measurement,the
other end to the open air (i.e. to atmospheric pressure). Differences in the height of the mercury
column in the two branches will indicate how much the pressure to be measured differs from atmospheric.
We have seen that the pressure in a fluid at a depth h, is given by
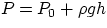
where P0 is the pressure at the surface. Suppose that we exert a force on a liquid (e.g. by means of a piston),
this force is going to be transmitted throughout the body of the liquid, and every section of the fluid will be
experiencing the same pressure increase. Formally, this effect is described by Pascal's principle:
the pressure applied at one point in one enclosed fluid is transmitted undiminished to every part
of the fluid and to the walls of the container
This property of fluids is exploited extensively in hydraulic lifts, etc.
Food for thought:
even though a hydraulic press allows to lift a heavy weight with little effort, there is no
violation of energy (and work) conservation. You can convince yourself of this by figuring out the
total displacement of the two sides of the hydraulic lift (and you can figure this out by
thinking in terms of the volume of fluid being displaced).
Archimedes' Principle
The story goes that, while floating in his bathtub, Archimedes saw the solution to a problem that his
"boss", the king of Syracuse, has posed to him, i.e. how to determine whether a crown was made of pure
gold without taking it apart. It is said that the thought occurred to him from noticing that the more he
immersed his body into the water, the more the water level rose. We can recognize two steps into Archimedes'
reasoning:
- 1.
- how to measure the volume (and therefore the density) of an object of irregular shape? Answer: fill
a container with liquid up to a certain level, fully immerse the body in it, and measure the new liquid level.
The height increase times the container's cross section gives the volume of the object. Density of the
material can then be found from
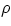 = m/V.
= m/V.
- 2.
- under what conditions will a body float or sink? Here the reasoning is the following : we start from
the previous result, i.e. an immersed body displaces an amount of liquid equal to its volume. When the body
is not in the liquid, the
liquid is in equilibrium, therefore each volume of water feels a force equal and opposite to its own weight.
When the body is immersed, nothing in principle changes, therefore the body will feel an upward force equal
to.... the weight of the amount of water it displaces.
Applying this result, we can immediately find the correct condition for floating or sinking :
a body immersed in a fluid (which could equally well be a liquid or a gas) is
subjected to its own weight, 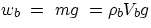 , and to the Archimedean push,
, and to the Archimedean push, 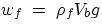 .The condition of equilibrium is then
.The condition of equilibrium is then
wb =
wf, i.e.
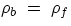
If the body's (average) density is less than that of the fluid the body will float, if it is more it will
sink. It is also straightforward to find what portion of a floating body is submersed : if we call Vs the
submersed portion for a body of total volume V, one has (can you prove it?):
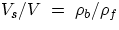
which is <1 when
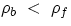
Fluidodynamics
In general, the motion of a fluid is a rather complicated phenomenon (think of white-water
rapids, or a boiling pot or the air and sewaves in a heavy storm, etc.). But in many situations we
can make simplifying assumptions and obtain some general results concerning the motion of fluids. In the
following we will assume that the fluid is
- incompressible, i.e. it has constant density (this is a very good assumption for
liquids, but it has to be handled carefully when dealing with gases)
- non-viscous, i.e. there is no internal friction among layers
- irrotational, i.e. the flow is such that the paths of different fluid particles do not intersect
each other. This type of flow is usually called laminar flow, and the non-laminar case is called
turbulent.
The first result we btain when these conditions are (at least approximately) satisfied, is how the
velocity of a fluid changes as it goes through a path of variable cross-section. Let's consider a fluid flowing
through a conduit of cross-section A. If V is the volume of fluid that goes through a section of the conduit in
the time 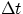 , one has
, one has
V = A x = A v
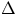
t
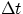 .But given that the total amount of fluid is conserved, and that the fluid is not compressible, this quantity has
to be the same everywhere along the fluid's path, i.e., if we take two positions of cross-section A1 and A2
we have
that shows how the speed of the flow increases as the fluid encounters a region of narrower cross section, or it
decreases in wider regions. This result goes under the name of continuity equation.
.But given that the total amount of fluid is conserved, and that the fluid is not compressible, this quantity has
to be the same everywhere along the fluid's path, i.e., if we take two positions of cross-section A1 and A2
we have
that shows how the speed of the flow increases as the fluid encounters a region of narrower cross section, or it
decreases in wider regions. This result goes under the name of continuity equation.
The next result, i.e. an expressions that relates pressure to velocity, is somewhat less intuitive, but it has
extremely far-reaching consequences and applications. To derive the result (known as Bernoulli's equation)
one has to apply to the fluid's motion the work-energy theorem, stating that the change in mechanical energy of
a system is given by the net work performed by non-conservative forces. If we consider a small volume of fluid
at positions 1 and 2, the change in mechanical energy is given by
(1/2mv12+mgy1) - (1/2mv22+mgy2)
The non conservative forces doing the work are effectively represented by the pressure in the fluid, and net
work will be done if there is a net pressure differential 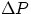 between the two faces of our fluid element.
If our small volume of fluid moves through a distance s, the net work done is
After a few simple step, one gets
between the two faces of our fluid element.
If our small volume of fluid moves through a distance s, the net work done is
After a few simple step, one gets
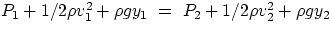
= constant
In the general case, each of the three terms has to be taken into account. But it
is useful to consider a couple of special cases :
- 1.
- flow through a pipe of constant cross section. In this case the continuity equation ensures that
v1=v2, therefore we get
i.e. the same result we had already found for the static case
- 2.
- horizontal flow, y=const. In this case we get
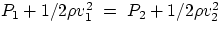
= constant
which tells us that in a fluid moving horizontally, an increase in velocity is accompanied by a decrease
in pressure.
Consequences and Applications:
- airplane lift
- atomizer
- curved balls
- roof blowing off in strong winds (Quick Quiz 15.10)
- Venturi meters (to measure fluid speed, e.g. speed of airplane w.r.t. surrounding air, or speed of fluid in
a pipe)
- prairie dog tunnel ventilation (Question 15.22)
- etc.



Next: About this document ...
Sergio Conetti
11/8/2000
![]() , with
h the height of the air column (some tens of kilometers), would not give the right answer, since
the density is not constant (you all know that there is "less air" at higher altitudes).
, with
h the height of the air column (some tens of kilometers), would not give the right answer, since
the density is not constant (you all know that there is "less air" at higher altitudes).