


Next: About this document ...
CHAPTER 16
Waves
In most cases, a wave can be thought of as a disturbance in a medium, propagating through it
(I say "in most cases" because a very importants class of waves is that of electromagnetic waves, that do not
need a medium to propagate; what is "disturbed" is the value of the electromagnetic field)
Another useful way to think of a wave is that it represents a transfer of energy without any net transfer
of material.
So let us focus on waves propagating through a material. In the following, we might consider either a single
wave pulse (flicking a rope once, the "wave" in a stadium, a short sharp sound, etc), or continuous waves
(waves in the sea, seismic waves during the duration of an earthquake, prolonged sound, etc.).
The first thing to notice is that, for a given direction of wave propagation, the local displacement of the medium can be
either perpendicular or parallel to the wave direction; we refer to the two cases as transversal or
longitudinal waves respectively. In some case, one can have a combination of both: in a wavy sea, water particle actually
move around little circles, therefore the wave has both a transversal and a longitudinal component.
Mathematical Description of a Wave : Wave Function
When dealing with waves, a complete description will include
both temporal and spatial coordinates. Let us think for instance of a wavy sea; one could do the following steps :
- 1.
- take a snapshot of the whole scene at a given instant; if y is the coordinate perpendicular to the sea surface, in
a given direction x the whole scene is represented by a function y=f(x)
- 2.
- alternatively, one could consider a fixed point in the sea (e.g. at the location of a buoy). As the buoy bobs up and
down, its motion (therefore the motion of the wave) is represented by a function y=g(t)
To get the complete description, one would have to take both pictures into account, therefore the wave will be fully
described by a function y=h(x,t). Next we will see that, for a well behaved wave (i.e. for a wave propagating with
constant velocity, as a wave travelling through a homogeneous medium does) the argument of the function describing
the displacement y must have a well defined form.
For simplicity, let us consider a single wave pulse moving with velocity v in the positive x direction. We will
consider two frames of reference a fixed one x, and another one x' moving together with the pulse. Let's also assume
that at t=0 the two frames coincide. The transformation between the two system is
x=x'+vt, y'=y
In the x frame, at t=0 the pulse shape will be described by some function y=f(x) . What is the correct function at any
later time t ? As the frame x' moves together with the pulse, one will always have y=f(x'). But x'=x-vt, therefore
y=f(x-vt)
Conclusion: an arbitrary wave (be it a pulse or continuous) moving with constant velocity in the positive x direction
will always be represented by a function of the type y=f(x-vt). Similarly, if the wave is moving in the negative x direction, its
wave function is y=f(x+vt).
Problem 16.3
Waves have the amusing property that when they meet, they go through each other without causing any permanent
damage. This is described by the Principle of Superposition :
if two traveling waves are described by the wave functions 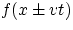 and
and 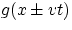 , then at any point the overall
wave function is h = f + g.
, then at any point the overall
wave function is h = f + g.
We can consider some extreme cases : take two wave pulses identical in shape but
opposite in sign traveling in opposite directions. From our assumptions, their wave functions are f(x-vt) and -f(x+vt).
The sum of the two will in general be some varying shape, except that, for t=0 their combination gives
f(x)+(-f(x) = 0) for all values of x
i.e. at that instant the pulses completely cancel each other : this is the standard condition of destructive
interference.
Similarly, we could have considered the case of the two pulses having the same sign: at the t=0 instant
the overall wave function is f(x)+f(x) = 2f(x),resulting in a pulse of the same shape but twice the amplitude at all
x's: here we have fully constructive interference.
Problem 16.9
The condition of having two identical pulses (either with the same orientation or flipped) traveling in opposite
directions can be realized in a rather straightforward way, because of the following property : when a wave encounters an
obstacle which prevents it from proceeding further, it will be reflected, i.e. it will travel in the opposite direction.
Thinking e.g. of a pulse traveling on a rope fixed at one end, one encounters two different situations :
- 1.
- if the end of the rope is not free to move at all, then the reflected pulse will be inverted
- 2.
- if on the contrary the end is free to move vertically (e.g. the end of the rope is attached to a light ring which is
free to slide along a pole), then the reflected pulse will have the same orientation as the incoming pulse.
An even more interesting phenomenon is observed when the wave reaches an interface between two media of different density
(in the case of a pulse traveling along a rope, this could be realized by joining a light rope with a heavy one).
When the wave reaches the interface, it is partially transmitted and partially reflected. The amplitude of the transmitted
and reflected waves is less than that of the original incoming wave, so as to conserve energy (see later). Moreover, the
reflected pulse will be inverted when the wave encounters a heavier medium, while it will keep the same orientation when
the encounterd medium is lighter.
Wave Speed We have already mentioned that a wave traveling through a homogeneous medium moves with constant
velocity. It is fairly straightforward to obtain an expression for the velocity in the case of a pulse traveling along a
rope. One can already get very close to the final answer by some intuitive considerations with some dimensional arguments:
- to start, we realize that a pulse will propagate along the rope only if the rope is under some tension T (if you have
a piece of rope lying on a table and shake one end, nothing will happen). One can also guess that the speed of propagation
will increase at the increase of the tension, since the tension provides the restoring force causing each element of the rope
to move back towards its position of equilibrium after it is disturbed.
- on the other side, the effect of the restoring force, i.e. the acceleration bringing each element of the rope back to
its undisturbed condition, will be impeded by the rope's inertia, i.e by its mass. Specifically, for an infinitesimal
rope element, the relevant quantity will be the mass per unit length
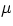 .
.
It is very reasonable to assume that there are no other factors determing the pulse propagation speed. If we now try to
combine the quantities T and 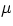 in an expression that has the dimension of a velocity, the only way we can do that
is with the expression
where C is a dimensionless factor. But it is easy enough to prove (see textbook page 500), that such a constant is not
required, and the correct expression for the wave speed is simply
This is a very general expression that applies to practically every possible medium, provided T and
in an expression that has the dimension of a velocity, the only way we can do that
is with the expression
where C is a dimensionless factor. But it is easy enough to prove (see textbook page 500), that such a constant is not
required, and the correct expression for the wave speed is simply
This is a very general expression that applies to practically every possible medium, provided T and 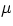 are interpreted
in each case as the appropriate "elasticity" term and "inertia" terms.
are interpreted
in each case as the appropriate "elasticity" term and "inertia" terms.
Sinusoidal Waves When dealing with harmonic motion, we had learnt that when energy is transferred to some elastic
object, the effect is to generate some oscillations well described by a sine function. Even though not stated explicitely,
in our previous study of harmonic motion we were dealing with the oscillating bodies as single points. In reality, when some
energy is transferred to an elastic object, the effect will be to generate some ripples (waves) propagating with some velocity
v through the object, and every point affected by the wave will move with simple harmonic motion.
From our earlier discussion, we can expect that wave equation for the whole ensemble of harmonic ripples will be of the
form
c is some dimensionless constant, which can be determined by means of the following arguments :
To start, we notice that as a full wave crosses a particular location, a point at that location executes a full
oscillation. If 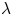 is the wavelength, defined, e.g., as the distance between two successive crests, and
T the period, i.e. the time to execute one whole oscillation, we have
This relation, which could also be written as
is the wavelength, defined, e.g., as the distance between two successive crests, and
T the period, i.e. the time to execute one whole oscillation, we have
This relation, which could also be written as 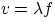 , where f = 1/T is the frequency, is true for any periodic wave,
and it applies to a very large class of situations (example : radio and TV stations can be identified either by
a frequency or by a wavelength. How can one convert from one to the other ?) Our equation can then be written as
Next, we can impose the condition of periodicity. We could do it in two ways, either demanding that the spatial part of
the equation represents a periodic wave of wavelength
, where f = 1/T is the frequency, is true for any periodic wave,
and it applies to a very large class of situations (example : radio and TV stations can be identified either by
a frequency or by a wavelength. How can one convert from one to the other ?) Our equation can then be written as
Next, we can impose the condition of periodicity. We could do it in two ways, either demanding that the spatial part of
the equation represents a periodic wave of wavelength 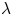 or that the temporal part represents a periodic
oscillation of period T . We will follow the first route, the second would yield an identical result (you can try it as an
exercise).
or that the temporal part represents a periodic
oscillation of period T . We will follow the first route, the second would yield an identical result (you can try it as an
exercise).
Like before, we can simplify the task by taking a snapshot at an arbitrary time, e.g. t=0. The condition we want to impose
is that when x increases by an amount  , the argument of the sine increases by
, the argument of the sine increases by 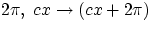 , i.e.
and our wave equation becomes
To make your life more complicated, physicists like to write this expression in a different form which, although formally
simpler, makes use of two quantities whose meaning is not as intuitive as the standard
, i.e.
and our wave equation becomes
To make your life more complicated, physicists like to write this expression in a different form which, although formally
simpler, makes use of two quantities whose meaning is not as intuitive as the standard 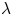 and T. Specifically,
if one defines the quantities
and T. Specifically,
if one defines the quantities
- angular wave number
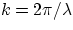 , and
, and
- angular frequency
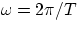
the wave equation becomes
and one also has
Finally, we should notice that out wave equation represents a specific choice for the origin of time/space coordinates, i.e.
a case such that at t=0 and x=0, y=0. To represents the most general case, we should allow for a possible phase
term, i.e. we should write the equation as
Transversal Velocity and Acceleration Knowledge of the wave equation allows us to obtain expressions for the
(transversal) velocity and acceleration of any point in a sinusoidal wave (Warning : do not confuse the velocity of a point
of the wave in its up/down harmonic motion with the wave propagation velocity). From ![$y(x,t)=A\sin [2\pi(x/ \lambda\pm t/T)] $](img14.gif) we have
we have
![$v_{y}(x,t)= \partial y/\partial t = -2\pi A/T\cos [2\pi (x/ \lambda\pm t/T)] $](img20.gif)
,
![$a_{y}(x,t)= \partial v_{y}/\partial t = -(2\pi /T)^2 A\sin [2\pi(x/ \lambda\pm t/T)] $](img21.gif)
which resemble the expressions we had found for velocity and acceleration in the harmonic motion (as it should be, since each
point along the wave does move with simple harmonic motion).
Energy in a Wave Youwere told that a wave can be thought of as a mean of transferring energy. We can now
establish how much energy is carried by a sinusoidal wave of given amplitude, wavelength and period. At any instant, the
wave possesses both kinetic and (elastic) potential energy. In your textbook, it is shown that the amount of potential
energy contained in one full wavelength of an oscillating string is given by
where 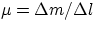 is the string's mass per unit length. The book also states that the same expression also
represents the total kinetic energy in one wavelength. For completeness, here is how to derive the expression for the Kinetic
Energy:
is the string's mass per unit length. The book also states that the same expression also
represents the total kinetic energy in one wavelength. For completeness, here is how to derive the expression for the Kinetic
Energy:
the kinetic energy in one infinitesimal section of string is
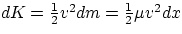
,
where v is
the transversal velocity of the string element. At t=0 the transversal velocity at any location x is
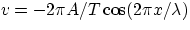 . We then have
Remembering that
. We then have
Remembering that 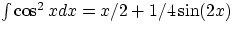 , one can reach with a few steps the final result
The total energy is then
, one can reach with a few steps the final result
The total energy is then  , while the total power transported during one period is
Notice that both energy and power depend on the square of the amplitude.
, while the total power transported during one period is
Notice that both energy and power depend on the square of the amplitude.
Section 16.9 : skip



Next: About this document ...
Sergio Conetti
11/13/2000
![]() and
and ![]() , then at any point the overall
wave function is h = f + g.
, then at any point the overall
wave function is h = f + g.