


Next: About this document ...
Chapter 18
Wave Superposition and Standing Waves
We have seen that when two (or more) waves meet, the resulting wave function is the sum of the individual
wave functions. Suppose you have two traveling sine waves of wavefunction ![$A\sin [2\pi (x/\lambda -t/T)]$](img1.gif) and
and ![$A\sin [2\pi (x/\lambda -t/T)+\phi ]$](img2.gif) . Using trigonometric identities one could see that their sum is
The resulting wave is still a traveling wave, whose amplitude is determined by the relative
phase
. Using trigonometric identities one could see that their sum is
The resulting wave is still a traveling wave, whose amplitude is determined by the relative
phase 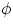 . The extreme cases are
. The extreme cases are
-
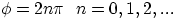 , leading to the largest amplitude 2A : this is fully constructive
interference
, leading to the largest amplitude 2A : this is fully constructive
interference
-
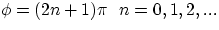 , the waves completely cancel each other, we have fully
destructive interference
, the waves completely cancel each other, we have fully
destructive interference
If we have two waves generated by two coherent (i.e. in phase) sorces, it should be possible to
observe interference phenomena at some distance from the sources. Specifically, one will have maximum
amplitude when the difference in path from the sources to the point of observation
is an integer multiple of wavelengths 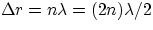 , while the condition
, while the condition
 will produce fully destructive interference. For a given geometry, measuring
the distance between regions of minimum and maximum amplitude allows to measure the wavelength of the wave
under exam (this is how it was determined that light is a wave).
will produce fully destructive interference. For a given geometry, measuring
the distance between regions of minimum and maximum amplitude allows to measure the wavelength of the wave
under exam (this is how it was determined that light is a wave).
Standing Waves
An interesting phenomenon occurs when two identical sine waves travel in opposite directions. This condition
can easily be realized by sending a continuous wave down a rope fixed at one end, resulting in the
combination of the generated wave and the reflected one. If ![$y_{1}=A\sin [2\pi (x/\lambda -t/T)]$](img9.gif) and
and
![$y_{2}=A\sin [2\pi (x/\lambda +t/T)]$](img10.gif) then
which does not represent any more a traveling wave. Instead
then
which does not represent any more a traveling wave. Instead
- at any given location x, each point performs harmonic oscillations. The period of oscillation is the
same for all values of x (all the points move in synchronism) but the oscillation amplitude is x-dependent,
according to
amplitude =
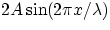
.
- in particular, when
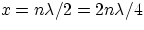 the amplitude is consistently zero for any value
of t. These points of zero displacement are called nodes
the amplitude is consistently zero for any value
of t. These points of zero displacement are called nodes
- the halfway points between nodes correspond to the location of maximum oscillation amplitude, these
are called antinodes and they occur for
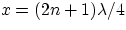
- even though a standing (or stationary) wave contains energy, the energy is not transmitted (the presence
of the nodes, which are always at rest, prevents any energy propagation). Still,
throughout the oscillation the energy undergoes a continuous transformation from potential to kinetic and
back.
Stringed Instruments: standing waves in a string fixed at both ends When some energy is transferred (e.g. by
plucking) to an elastic string of length L fixed at both ends, in principle all sort of different oscillation can be
generated, but only the ones corresponding to allowed standing waves will persist. The condition to be satisfied is very
straightforward : given that the extremes of the string are fixed, these will always be nodes. The distance between nodes
is always half a wavelength therefore, in order to have a node both at the beginning and at the end of the string, one must
fit within the length of the string an integer number of half wavelengths:
In terms of frequency (i.e. pitch of sound produced), since
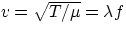 , we have
n=1 corresponds to the string's fundamental frequency (in this case
, we have
n=1 corresponds to the string's fundamental frequency (in this case 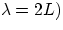 , while higher values of n
produce the higher order harmonics. The expression above also confirms the well known fact that one can change the
pitch of the sound generated by a given string either by changing its length or its tension (alternatively, one can use a
string of different
, while higher values of n
produce the higher order harmonics. The expression above also confirms the well known fact that one can change the
pitch of the sound generated by a given string either by changing its length or its tension (alternatively, one can use a
string of different 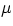 )
)
Resonance : we have already encountered it when studying forced oscillations. The idea is that the oscillations
of a system will reach maximum amplitude when a periodic force is applied to it of frequency close to one of the system's
natural frequencies. The effect is easily observable in sound phenomena.
Standing waves in air columns and in rods : read and digest the basic concepts
Beats : this effect is due to the interference of two waves of almost equal frequency. Choosing to perform the
observation at a specific x location, e.g. at x=0, the wave functions of two waves of frequencies f1 and f2 are
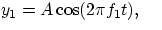
and
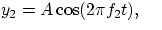
Applying the usual trigonometric identities, one gets for the sum wave function
this can be interpreted as a wave of frequency  and of periodically varying amplitude, the period of
the variation being
and of periodically varying amplitude, the period of
the variation being 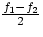 .
.
Fourier Analysis With the possible exceptions of a tuning fork (and, nowadays, of electronically generated sounds),
sound waves, even though of a well defined frequency, never correspond to a simple sine function. Even for simple musical
instruments, the produced sound will be a combination of the fundamental plus several higher order harmonics, each one
intervening with its own amplitude. The phenomenon can be interpreted in terms of Fourier's theorem :
any arbitrary periodic function of period T can be represented by a sum of sine (and cosine) waves of periods T/n, n=1,2,...,
Suitable choice of the amplitude coefficients Ak, Bk and of the number of terms to be included allows to represent any
arbitrary waveform.



Next: About this document ...
Sergio Conetti
11/17/2000