CHAPTER 2

2cKinematics 2cDynamics

1-dim many dim

Motion in one dimension : position of moving object is uniquely identified by a single number (x-coordinate, can be +ve or -ve)

Define : displacement = change in position = x_f - x_i

Do not confuse displacement with distance traveled (measured e.g. by your car's hodometer)

Note : even though the book states (correctly) that displacement is a vector, i.e a quantity identified by a magnitude and a sign, as long as we are dealing with one-dimensional motion we can ignore this fact, provided we are aware that displacement can be either +ve or -ve. Examples.

The details of any arbitrary motion are fully known if we can specify the position of our object at any given time :

x = f(t).

Examples 1,2,3.

Warning : do not confuse x vs. t with trajectory

Can we be more specific about how fast our object is moving ?

Yes, if we specify what is the displacement 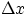$\Delta x$ in a given time interval $\Delta t$:

$v_{av} = \Delta x/\Delta t$

Examples 1,2,3

If the x vs t curve is a straight line, then v_av is the same for any choice of $\Delta t$ : one is dealing with a situation of constant velocity v_av = v =const. In this case, if x₀ is the position of an object at t=0, we can write the above expression as :

v = (x(t)-x₀)/t
x(t) = x₀ +vt

this is the general equation describing every possible one-dimensional motion with constant velocity.

What about two objects moving with different v's, x₀'s ? How many times (if any) will they meet, and where ?

Speed vs. velocity :

• velocity = displacement/time (+ve or -ve)
• speed = distance covered/time (always +ve)
  
  

Instantaneous velocity:

• $v = lim_{\Delta t\rightarrow 0} \Delta x/\Delta t = dx/dt$
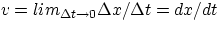
• slope of the tangent to the x vs t curve

Instantaneous speed = magnitude of instantaneous velocity

Motions with perfectly constant velocity are not a common occurence. To study more general cases we must introduce the concept of

ACCELERATION :
if at t₁ an object has velocity v₁ and at t₂ velocity v₂, then

$a_{av} = (v_{2}-v_{1})/(t_{2}-t_{1}) = \Delta v/\Delta t$

(note that a can be +ve or -ve). Problem 2.13



Lessons :

1.

signs are important and should not be ignored

2.

the actual value of the signs depends upon your (arbitrary) choice of what you call the positive direction. But, in any given problem, you must make this choice atthe beginning, and stick with it throughout the problem

Question : what is the sign of a in the problem above? Is it always the same, or does it flip as the ball changes direction?

Instantaneous acceleration

Following the same reasoning as before, we can define

$a = lim_{\Delta t\rightarrow 0} \Delta v/\Delta t = dv/dt$

and, consequently,

a = dv/dt = d/dt (dx/dt) = d²x/dt²

Motion with constant acceleration

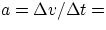
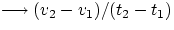
$a = \Delta v/\Delta t =$const $\longrightarrow (v_{2}-v_{1})/(t_{2}-t_{1})$ = const for any t₁,t₂.

Choose : t₁ = 0, then if v₀ is velocity at t=0,

a = (v(t)-v₀)/t

v(t) = v₀ + at

v(t) is a straight line in the v-t plane. In this case, one also has (since v_av = (v₀+v(t))/2) :

x(t) = x₀ + v_avt = ........

x(t) = x₀+v₀t+1/2 at²

How does the x vs t curve look like ? Suggested exercise : try plotting it for various values (+ve or -ve) of x₀, v₀, a.

What if we have two bodies, one moving with constant acceleration and the other with constant velocity? How many times will they meet and where ? Food for thought : look at book's example 2.8; the book considers only the +ve solution. This is correct in the example at hand. Why? Under what circumstances should one consider both solutions? Think about it, we will discuss it in the next lecture

Finally one can derive an expression relating only x,v,a (solve for time in the velocity formula, and substitute in the position formula). One gets

x(v) = x₀ + (v²-v²₀)/(2a)

Appropriate use of the three equations allows to solve any (solvable) problem of motion with constant acceleration.
Problem 2.56

Important case of motion with constant acceleration : free falling, i.e. motion under the sole influence of gravity. Galileo experiments showed that (and Newton explained why) bodies near the earth surface move with constant (downward directed) acceleration of 9.8 m/s² . All of the above equations apply to this situation.
More Calculus.
It should be possible to derive the equation of motion for constant acceleration just by applying our knowledge of calculus:

if a = dv/dt, then

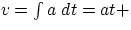
$v = \int a~dt = at +$ const = v₀ + at.

Similarly, since v = dx/dt,

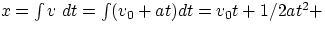
$x = \int v~dt = \int (v_{0}+at)dt = v_{0}t + 1/2 at^{2} +$ const = x₀ +v₀t + 1/2 at²