


Next: About this document ...
Chapter 20
Heat
For a long time, scientists did not have a clear idea of what heat, or, more precisely, heat transfer really
was. In fact, the most common belief was that heat was carried by some sort of intangible, mysterious fluid,
called either phlogiston or caloric. The eventual realization that heat transfer was in reality yet
another form of energy transfer
was a major milestone, that effectively opened up the road to the industrial revolution, the development of
steam engines, the science of Thermodynamics, etc. Interpreting heat as a form of energy transfer closed the loop
in most mechanical processes, showing that, whenever mechanical energy is lost (e.g. due to friction) in any
given process, an equivalent amount of energy is generated in the form of thermal energy, and this in turn
gives to the Principle of Energy Conservation a much much broader scope. Moreover, it was possible to introduce
the concept of internal energy, i.e. energy carried by the elementary constituents (e.g. atoms or molecules)
of any given substance.
Internal Energy : in the simplest case of a monoatomic gas (e.g. noble gases) internal energy can only be
present in the form of linear kinetic energy of the gas atoms. In general, internal energy will also include
rotational kinetic energy and electrostatic potential energy (for completeness, one could also list nuclear
potential energy as contributing to internal energy, but this energy plays no role in ordinary
thermodynamical processes).
In general, heat can be thought of as a transfer of internal energy from one object to another. This is equivalent to
the transfer of mechanical energy as mediated by work. In general, internal energy is related to temperature, and a
process of heat transfer is accompanied by a change of temperature, but, as we will see, there are some important
exceptions.
When studying heat transfers, it is more straightforward to deal with the unit originally introduced to
describe such phenomena, i.e. the calorie. 1 calorie is defined as the amount of heat required
to increase by one degree Celsius 1 gram of water (the exact defintion would state ....to bring 1 g of water
from 14.5 to 15.5 degrees). A related unit is the Calorie (notice the capital C), which is equal to
1000 calories, therefore it is the amount of heat required to increase by one degree the temperature of
1 kilogram of water ( or, to a good approximation, to increase the temperature of 100 g of water by 10 degrees,
etc.).
In the next step, we define the specific heat of any substance as the amount of heat (in
Calories) required to increase by 10C 1 kg of the substance. From these definitions it follows immediately
that the heat capacity of water, measured in Cal/(kg 0C), is 1. The heat capacity of water
is among the highest of most materials, it takes lots of heat to warm up water and conversely, hot or warm
water can store and release lots of heat.
From these definitions, it follows immediately that the quantity Q of heat involved in changing the temperature
of a body of mass m by an amount 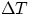 is given by
is given by
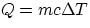
where c is the specific heat of the particular substance
When, through the work of scientists like Benjamin Thompson Count Rumford (a rare case of an American
emigrating to Europe) and James P. Joule, it was realized that heat was another form of energy transfer, it was
possible to obtain the exact correspondence between the traditional units for measuring heat and the
standard units for energy. And the answer was:
1 cal = 4.186 joules, or 1 Cal = 4186 joules
This result is extremely useful, since it allows us to work out how much weight lifting we need to do in
order to burn off a 100 Calorie snack ...
Phase Changes
Adding or removing heat to/from a substance will change its temperature up to a certain point : we all know
what happens to water when we heat it or cool it too much. The most important thing to remember when dealing
with phase changes is that, throughout the change the temperature remains constant. When we say that
water freezes at 00C, we mean that, if we have some water and lower its
temperature, when it reaches 0 it will stay at that value until all the water has frozen, and only then
removing more heat will further cool the sample.
Conversely, if we start with very cold ice and warm it up,
it will start melting when it reaches 00, and the ice/water mixture will remain at that temperature until
all the ice has melted. The same effect occurs when water boils away, i.e it turns into its
gaseous phase, at 1000C (but remember: the boiling point of a liquid depends on the pressure to which it is
subjected, in Denver water boils below 1000C).
The amount of heat that is involved in the phase change (the latent heat of fusion or of
vaporization) is considerable: the latent heat of fusion for water is 79.7 cal/g (or Cal/kg),
which means for instance that it takes the same amount of heat to melt 1 kg of ice originally at
00C as to increase its temperature from 0 to  800 !!!. Similarly, the latent heat of
evaporation for water is 539 cal/g .
800 !!!. Similarly, the latent heat of
evaporation for water is 539 cal/g .
Remember that the process goes both way: if e.g. lots of heat is required to vaporize
liquid water at 1000, condensing steam will release an equivalent amount of heat: a burn can be much more
severe when caused by steam rather than water at 1000C.
Energy Conservation : 1st Law of Thermodynamics
To start, we note that, if a system has some internal energy then (almost by definition) it is capable of doing work.
Recalling that work is Force x displacement, we realize that an expanding gas does work; the force at play comes from
the gas pressure, and the displacement can be that of a piston, or of the molecules of another gas, or the walls of a
stretchable container, etc. (exception: a gas expanding into a vacuum does not displace anything therefore it does no
work). Choosing the simple case of a gas in a cylindrical container with a movable piston of area A
dW =
F dx =
PA dx =
P dV
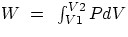
notice that in general the work done does depend on the path followed to go from V1 to V2 . Examples :
start from (P1,V1) and reach (P2,V2) and compare compare the work done
- either when the process occurs at constant temperature (therefore PV = nRT =costant)
- or when first allowing to expand at constant pressure and then reducing the pressure (e.g. by reducing the
temperature) while keeping the volume constant
In spite of the fact that work depends upon the path followed, we can still introduce the idea of energy conservation in
a thermodynamical process.
Let us first clarify a confusing issue concerning the signs of the quantities involved : we are
interested in finding the change in the internal energy of our system 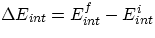 . A change in
internal energy can occur
. A change in
internal energy can occur
- by transfering some amount of heat Q in or out of the system
- or when some work W is done onto or by the system
It is rather intuitive that Eint will increase 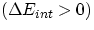 if we
if we
- either transfer heat into the system, or
- do some work onto the the system
For both of these cases Q and W will then be positive. Conversely, Eint will decrease 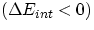 if we
if we
- transfer heat out of the system, or
- the system itself does some work
In these cases, Q and W will be negative. Having clarified this, we can write the condition of energy conservation as
with the understanding that both Q and W can be positive or negative, according to the intuitive rules discussed above.
Note: "my" sign convention is different from the one given in the book, but, in my opinion, it is less confusing. Using
my convention, when facing a particular problem and needing to assign signs to W and Q, you should ask yourself (separately
for Q and W) : is this process going to increase or decrease the internal energy? and assign the signs accordingly.
Notice also that in "my" convention, Q and 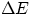 have the same sign as the book, while W has the opposite sign.
have the same sign as the book, while W has the opposite sign.
Problem 20.40
A few special cases:
- adiabatic = no heat exchange with the environment:
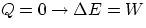
- isovolumetric or isochoric :
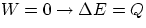
- isobaric :

- isothermic : PV = nRT = constant,
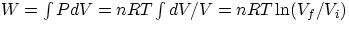
Heat Transmission
Heat Transmission con occur via Convection, Conduction or Radiation. Convection is the dominant
process in fluids (liquids and gases), Conduction acts mostly in solids (but also in liquids and, to some
extent, in gases). Heat transfer by radiation can take place through a vacuum , as well as through any
medium transparent to radiation.
Convection
The mechanism for convection is the density difference in regions of a fluid at different temperatures,
and the consequent action of gravity. Take a fluid at a constant temperature throughout and heat some
region of it. In the warmer region density will decrease and the fluid in that region will rise (according
to Archimedes principle). Simultaneously, cooler fluid will move in to fill in the space vacated by the
warmer fluid. The effect of such convective currents is the transport of thermal energy throughout
the fluid.
Typical instances of convection are e.g. water being heated in a pan or the formation of cumulus clouds.
In several applications, one can also have forced convection, e.g. when using a fan or a pump
(to be correct, the radiator in you car should not be called Radiator but "Convector").
Although conceptually easy to understand, it is not easy to describe convection in a quantitative way.
Conduction
While in convection heat is carried by an actual displacement of matter within the fluid, in conduction
only heat is transferred, without any transportation of matter taking place. To interpret the phenomenon
of heat conduction at the atomic level, we should be aware that temperature of a body is related to the
average kinetic energy of its molecules. In the contact region between a colder and a warmer body,
collisions among molecules will have the effect of transfering some of the (thermal) energy from the higher
to the lower temperature.
But to analyze heat conduction quantitatively it is not necessary to think in terms of collisions among
molecules. Instead, we can easily write the basic expression representing the amount of heat Q transmitted
across a given thickness of material :
where A is the area of two surfaces which are at a temperature difference 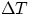 , L is the material
thickness and t is the elapsed time. k is a constant, typical of the material, which represents how well
(or how badly) the material can transmit heat. According to the application, we will want to
employ either very good conductors (e.g. in a frying pan) or good insulators (for the pan's handle).
Remembering that Q is an energy, and that Power = Energy/time, the power transmitted by conduction is
, L is the material
thickness and t is the elapsed time. k is a constant, typical of the material, which represents how well
(or how badly) the material can transmit heat. According to the application, we will want to
employ either very good conductors (e.g. in a frying pan) or good insulators (for the pan's handle).
Remembering that Q is an energy, and that Power = Energy/time, the power transmitted by conduction is
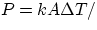
L
In many applications, dealing mainly with construction and home insulation, the expression above is
written as
with R, the R-value, = L/k . R is useful to compare simultaneously insulating power and
material thickness; obviously the larger is R, the better the insulation.
It is also useful to remember that air (especially dry air) is a good insulator, while
water is a good conductor (on a windless day, you could stand in 500F air without too much discomfort,
but you would quickly get very chilled if you were in water of the same temperature).
When dealing with conduction across layers of different material, the useful rule to remember is that,
at equilibrium, the same amount of heat has to go through each material.
Radiation
Every object, no matter at how low a temperature (except for absolute zero) emits some
amount of energy in the form of electromagnetic radiation, i.e. electromagnetic
waves. We haven't yet studied electromagnetism, but for now let us just accept the
idea that electromagnetic waves (corresponding to oscillations of the electromagnetic field) can manifest themselves
in many different forms, ranging from, in
increasing energy, radio waves, microwaves, infrared, light, ultraviolet, X-rays and
gamma-rays. The member of this family usually associated with heat and temperature is the infrared
radiation, since this type of radiation is felt by our bodies as heat, and the range of
radiation emitted by bodies at ordinary temperatures is peaked mainly in the infrared region (but all
other types of electromagnetic radiation do transfer energy and consequently increase the temperature of
an object, you can get burnt equally well by a laser producing purely visible light or by UV rays).
If a body at a given temperature continuously emits radiation, that is if it emits some of its internal
energy, then, if left to itself, it would gradually cool down (this is in fact what happens
if we have a hot body in a cooler room). But, when in equilibrium with its surroundings, an object
maintains its temperature; this must mean that the body, in addition to radiating away energy, must also
be able to absorb it from its surroundings.
And this is exactly what happens: when in thermal equilibrium
with its surroundings a body at the same time absorbs and emits radiation at the rate of
P = Power = Energy/time = Q/t =
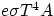
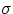 is a universal constant, and e is a number between 0 and 1 that depends upon the properties of the
emitting/absorbing surface.
is a universal constant, and e is a number between 0 and 1 that depends upon the properties of the
emitting/absorbing surface.
It is important to understand the role and meaning of e : let's take a certain object, and "shine" it with
a certain amount of electromagnetic radiation (e.g. light, or infrared, etc.). Experience tells us that
different objects will absorb the radiation in different amounts : we define as emissivity e the
ratio of energy absorbed by the body to the energy received by it. Obviously e will range
between 0 and 1 (and what happens to the energy that is not absorbed? it is reflected).
Now you would be entitled to ask : why did I call this ratio emissivity and not, e.g. absorptivity
? The reason is that there is a one to one correspondance between energy absorbed and energy emitted :
the rate of energy that a body absorbs is identical (for the same temperature) to the rate it will emit,
i.e. the formula above applies equally well to emission and absorption. But do not be confused: the actual
value of emitted energy depends upon the temperature of the emitting body, while that of absorbed energy
depends upon the "temperature" of the energy reaching the body. In formula



Next: About this document ...
Sergio Conetti
12/5/2000